Содержание
- 2. План урока Вступление Какие бывают системы счисления Непозиционные системы счисления Единичная система счисления Древнеегипетская система счисления
- 3. «Всё есть число» Так говорили древние пифагорейцы. Что они имели в виду? Этой фразой пифагорейцы подчеркивали
- 4. Определения Цифры Число Система счисления – это символы, участвующие в записи числа и составляющие некоторый алфавит.
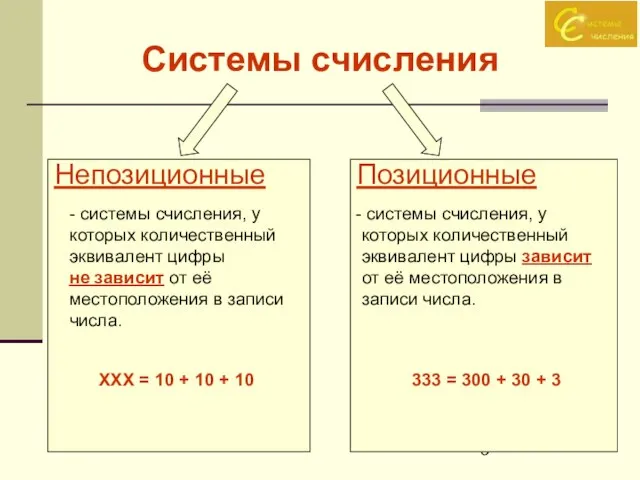
- 5. Системы счисления Непозиционные Позиционные - системы счисления, у которых количественный эквивалент цифры не зависит от её
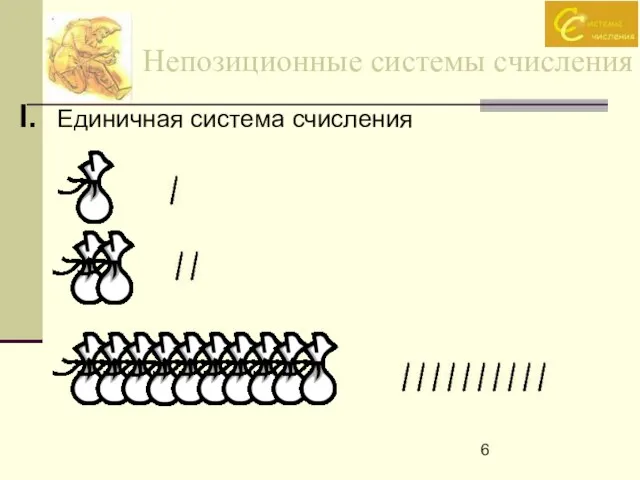
- 6. Непозиционные системы счисления I. Единичная система счисления
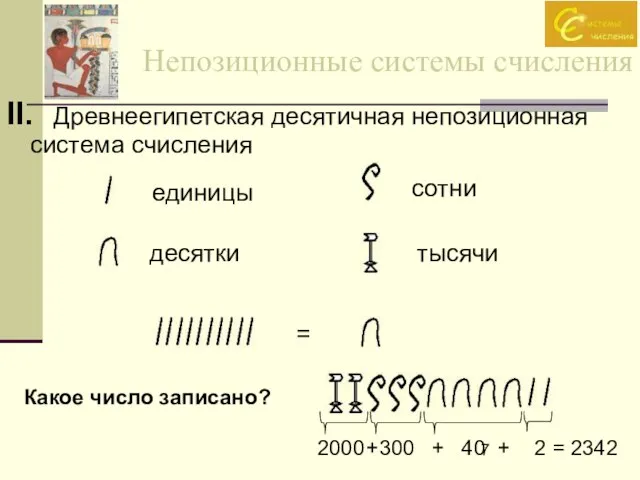
- 7. II. Древнеегипетская десятичная непозиционная система счисления Непозиционные системы счисления 2000 300 40 2 единицы десятки сотни
- 8. Непозиционные системы счисления III. Римская система счисления I – 1, V – 5, X – 10,
- 9. Непозиционные системы счисления III. Римская система счисления I – 1, V – 5, X – 10,
- 10. Непозиционные системы счисления III. Римская система счисления I – 1, V – 5, X – 10,
- 11. Непозиционные системы счисления IV. Греческая система счисления Γ Δ Η Χ Μ - 5 - 10
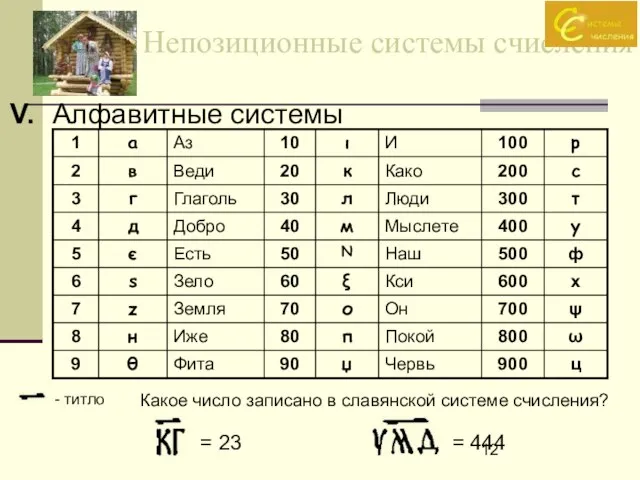
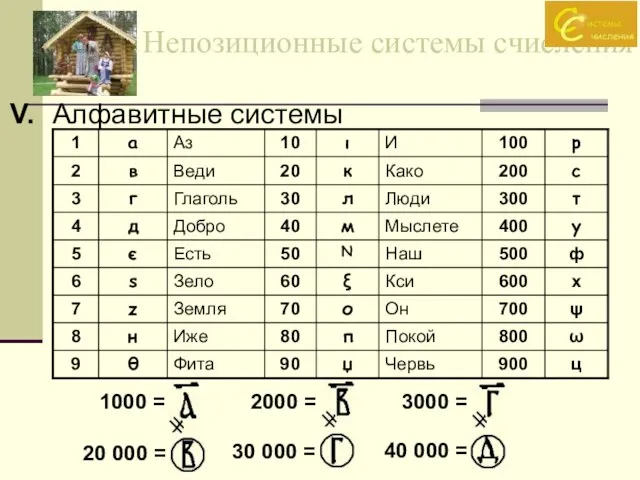
- 12. Непозиционные системы счисления V. Алфавитные системы - титло Какое число записано в славянской системе счисления? =
- 13. Непозиционные системы счисления V. Алфавитные системы 1000 = 2000 = 3000 = 20 000 = 30
- 14. Непозиционные системы счисления Каковы недостатки непозиционных систем счисления? В записи больших чисел участвует большое количество цифр.
- 15. Позиционные системы счисления Основные достоинства позиционной системы счисления: Простота выполнения арифметических операций. Ограниченное количество символов, необходимых
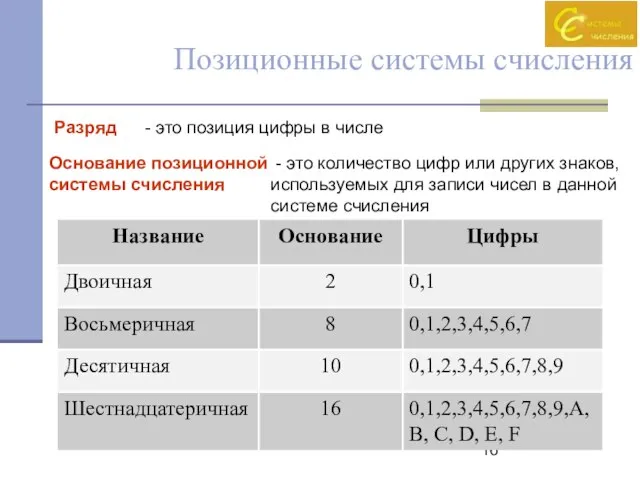
- 16. Разряд Основание позиционной системы счисления - это позиция цифры в числе - это количество цифр или
- 17. В позиционной системе счисления любое вещественное число может быть представлено в виде: Aq = (an-1qn-1+an-2qn-2+…a0q0+a-1q-1+a-2q-2+…a-mq-m) -
- 18. Позиционные системы счисления В позиционной системе счисления любое вещественное число может быть представлено в виде: Aq
- 19. Позиционные системы счисления В позиционной системе счисления любое вещественное число может быть представлено в виде: Aq
- 20. Позиционные системы счисления Свернутой формой записи числа называется запись в виде: A = an-1 an-2 …
- 22. Скачать презентацию













 Вредные привычки
Вредные привычки Этнос и нация 11 класс
Этнос и нация 11 класс ПП-451 представляет
ПП-451 представляет К 50-летию полёта Ю.А. Гагарина в космос
К 50-летию полёта Ю.А. Гагарина в космос Питание в Средневековье
Питание в Средневековье «Знакомство с цифрой 8»
«Знакомство с цифрой 8» по морям по волнам
по морям по волнам Виды конституций
Виды конституций Информационные технологии в экономике
Информационные технологии в экономике  Куст Сирени
Куст Сирени Подвижная игрушка Слоненок
Подвижная игрушка Слоненок Тимофеев М.Т. к.ю.н., доцент кафедры государственно-правовых дисциплин СЗФ РПА Минюста России, правовой эксперт СПб ОО «Граждански
Тимофеев М.Т. к.ю.н., доцент кафедры государственно-правовых дисциплин СЗФ РПА Минюста России, правовой эксперт СПб ОО «Граждански Рациональные мотивы
Рациональные мотивы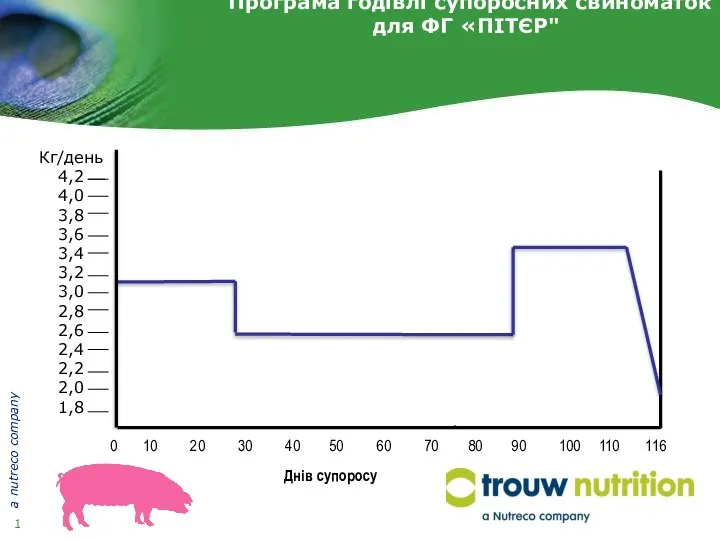 Програма годівлі супоросних свиноматок для ФГ ПІТЄР
Програма годівлі супоросних свиноматок для ФГ ПІТЄР Публичный отчет директора школы №753Патрикеевой И.Е.
Публичный отчет директора школы №753Патрикеевой И.Е. Развиваем речь ребенка ч 2
Развиваем речь ребенка ч 2 Основы стандартизации. Техническое регулирование
Основы стандартизации. Техническое регулирование МАКА в таблетках
МАКА в таблетках Организация досуга для лиц с нарушением интеллекта
Организация досуга для лиц с нарушением интеллекта Юридические факты
Юридические факты Особенности ведения деловых переговоров в Китае
Особенности ведения деловых переговоров в Китае Внутренние воды
Внутренние воды Projekt Aktywizacji Seniorów
Projekt Aktywizacji Seniorów Евгений Иванович Чарушин
Евгений Иванович Чарушин Спринт 2
Спринт 2 Информационно-коммуникационные технологии – инструментарий универсальных учебных действий и деятельностный подход в предметах
Информационно-коммуникационные технологии – инструментарий универсальных учебных действий и деятельностный подход в предметах  ГИДРОСФЕРА
ГИДРОСФЕРА Time Management
Time Management