Содержание
- 2. Случайные величины обозначаются греческими буквами: ξ (кси), η (эта), θ (тета) и так далее, а их
- 3. Случайные величины делятся на дискретные; непрерывные. Случайную величину ξ называют дискретной, если множество ее возможных значений
- 4. Непрерывные случайные величины сплошь заполняют некоторый числовой интервал. Например, время безотказной работы прибора теоретически [0; ,+∞)
- 5. Дискретные случайные величины задаются рядом распределения, а непрерывные – функцией распределения
- 6. Ряд распределения Ряд распределения ставит в соответствие каждому возможному значению случайной величины хi соответствующую вероятность рi.
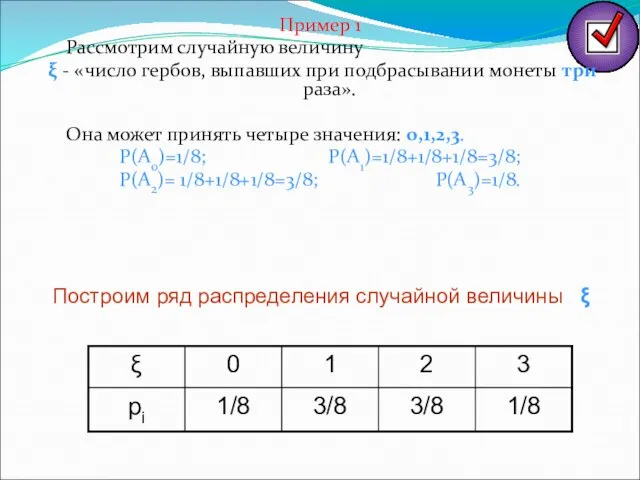
- 7. Пример 1 Рассмотрим случайную величину ξ - «число гербов, выпавших при подбрасывании монеты три раза». Она
- 8. Функцией распределения F(х) СВ ξ называется функция действительного аргумента х, определенная на всей числовой оси и
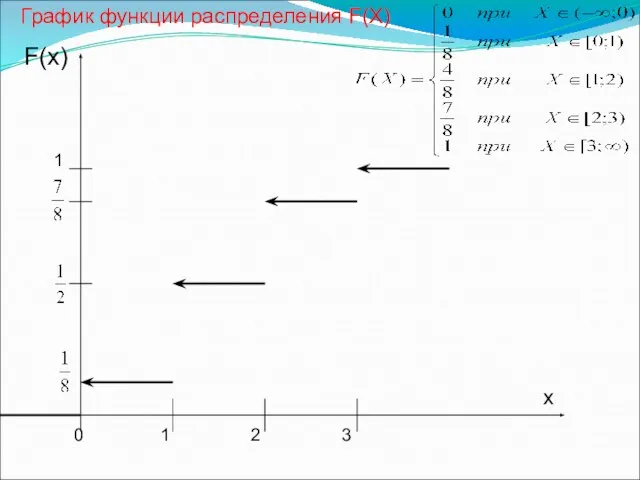
- 9. Пример Построить функцию распределения числа гербов при трех подбрасываниях монеты Решение -∞ 0 ≤x 1 ≤x
- 10. 1 F(x) График функции распределения F(X) 0 1 2 3 х
- 11. Свойства функции распределения 1) 2) F(x)–неубывающая: если то F(x1) ≤ F(x2). 3) 4) Вероятность попадания СВ
- 12. Пример СВ задана функцией распределения Найти вероятность того, что в результате эксперимента случайная величина попадет в
- 13. Самостоятельная работа Задание. Случайная величина задана функцией распределения. Найти вероятность попадания в интервал (1;2].
- 14. Сверим ответы? У нас a=1; b=2. Тогда
- 15. Плотность распределения вероятностей Справедливо и обратное соотношение:
- 16. Свойства плотности распределения вероятностей 1) Для всех x плотность распределения вероятностей неотрицательна 2) Свойство нормировки .
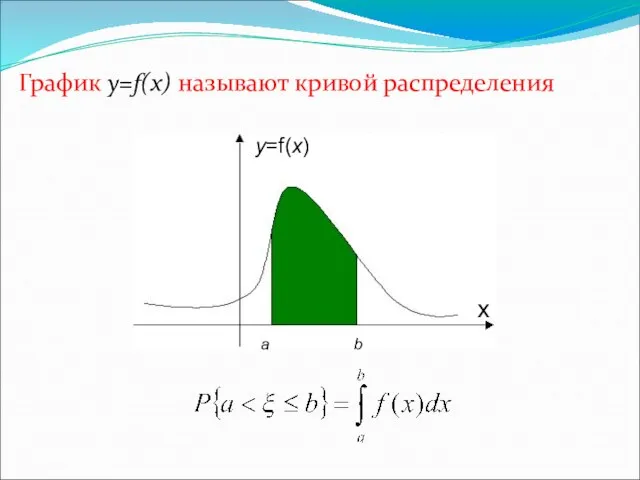
- 17. График y=f(x) называют кривой распределения y=f(x) a b х
- 18. Пример Случайная величина задана плотностью вероятности Найти вероятность того, что в результате эксперимента случайная величина попадет
- 19. Числовые характеристики СВ Это числа, полученные по определенным правилам из законов распределения. Наиболее часто используются: Математическое
- 20. Математическое ожидание СВ Характеризует среднее значение СВ Математическим ожиданием дискретной СВ ξ называется сумма произведений возможных
- 21. M(ξ) = x1 p1 +x2 p2 +… xn pn Пример Найти математическое ожидание числа очков при
- 22. Математическим ожиданием M(ξ) непрерывной случайной величины ξ с плотностью вероятности называется интеграл , Пример Найти математическое
- 23. Решение
- 24. Дисперсия случайной величины Дисперсия и среднеквадратическое отклонение определяют среднюю величину разброса значений СВ относительно математического ожидания
- 25. Дисперсия непрерывной СВ определяется формулой или Для дискретной СВ дисперсия определяется по формуле или
- 26. Пример Найти дисперсию числа очков при одном подбрасывании кубика. Решение M(ξ)=3,5
- 27. Пример Найти дисперсию случайной величины, заданной плотностью вероятности Решение
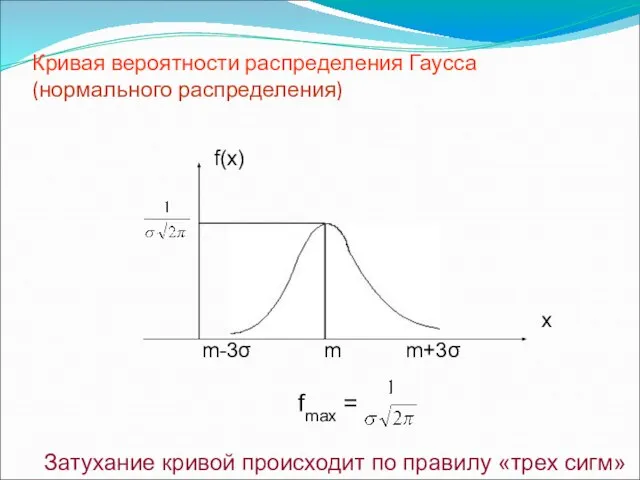
- 28. Нормальный закон распределения СВ Случайная величина ξ имеет нормальное распределение, если ее плотность распределения вероятностей при
- 29. Кривая вероятности распределения Гаусса (нормального распределения) f(x) x m m-3σ m+3σ fmax = Затухание кривой происходит
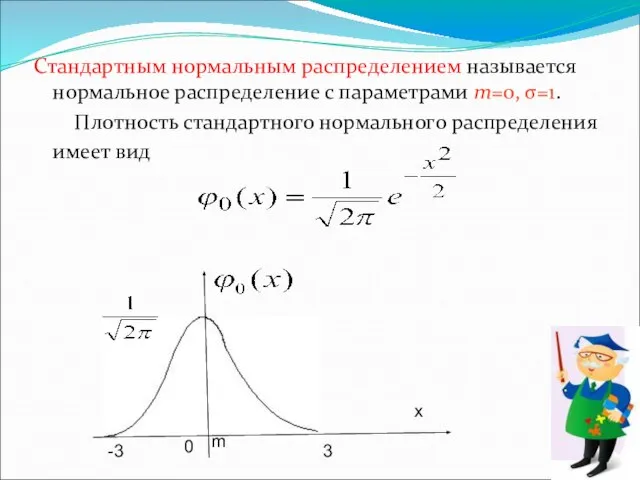
- 30. Стандартным нормальным распределением называется нормальное распределение с параметрами m=0, σ=1. Плотность стандартного нормального распределения имеет вид
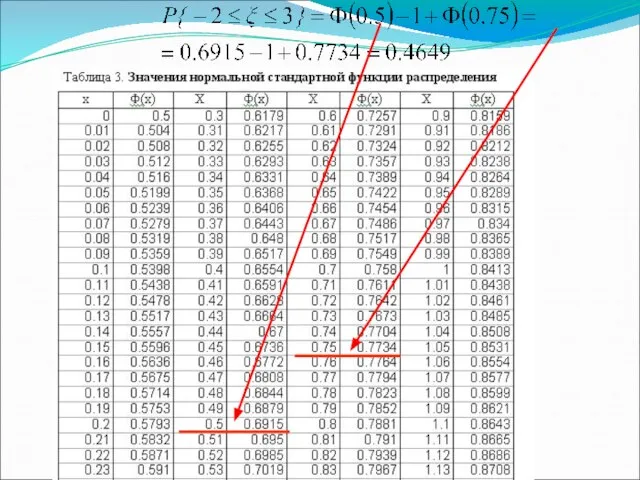
- 31. Функцию распределения стандартного нормального закона называют функцией Лапласа Для функции распределения стандартного нормального закона имеются таблицы
- 32. Пример Случайная величина задана плотностью вероятности Определить: математическое ожидание; дисперсию; стандартное отклонение; вероятность попадания значений случайной
- 33. Пример Случайная величина задана плотностью вероятности Определить: математическое ожидание; дисперсию; стандартное отклонение; вероятность попадания значений случайной
- 34. Пример Случайная величина задана плотностью вероятности Определить: математическое ожидание; дисперсию; стандартное отклонение; вероятность попадания значений случайной
- 35. Пример Случайная величина задана плотностью вероятности Определить: математическое ожидание; дисперсию; стандартное отклонение; вероятность попадания значений случайной
- 36. a=-2; b=3
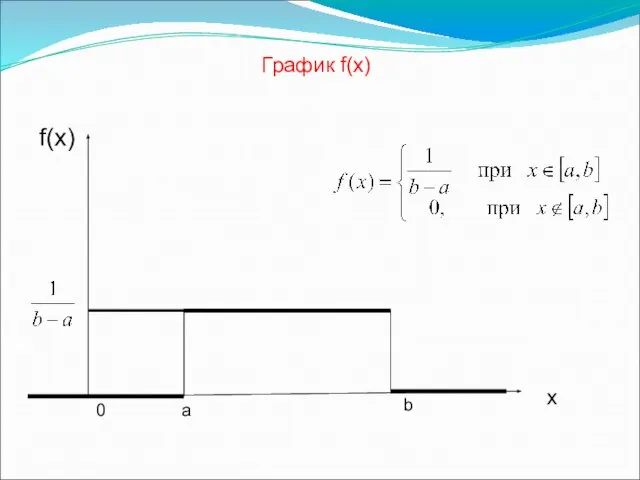
- 38. Случайная величина ξ распределена равномерно на промежутке [a,b], если ее плотность распределения вероятностей задается равенством Равномерное
- 39. f(x) График f(х) 0 х a b
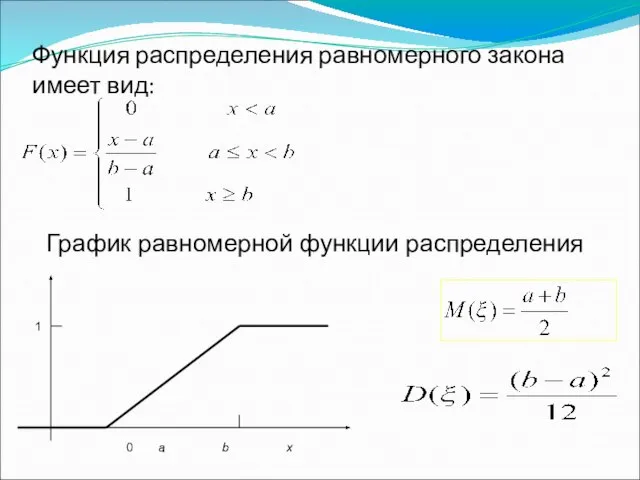
- 40. Функция распределения равномерного закона имеет вид: График равномерной функции распределения
- 41. Вероятность того, что случайная величина η (число «успехов» при n независимых испытаниях) примет значение m, можно
- 42. Пример В коробку сложили 3 изделия. Вероятность, что изделие - бракованное, равна 0,1. Найти математическое ожидание
- 43. если ее плотность распределения вероятностей задается равенством Показательное распределение Функция распределения показательного закона имеет вид:
- 45. Скачать презентацию









![Самостоятельная работа Задание. Случайная величина задана функцией распределения. Найти вероятность попадания в интервал (1;2].](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/384975/slide-12.jpg)




















![Случайная величина ξ распределена равномерно на промежутке [a,b], если ее плотность распределения](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/384975/slide-37.jpg)



 Презентация на тему Олимпийские игры в Москве 1980
Презентация на тему Олимпийские игры в Москве 1980  Национализм как политическая идеология
Национализм как политическая идеология Презентация на тему Решение задач на нахождение площади поверхности и объемов тел вращения
Презентация на тему Решение задач на нахождение площади поверхности и объемов тел вращения  Moderní cukrovar HROCHŮV TÝNEC
Moderní cukrovar HROCHŮV TÝNEC Система работы учителя математики с родителями при подготовке учащихся к государственной итоговой аттестации в форме ЕГЭ
Система работы учителя математики с родителями при подготовке учащихся к государственной итоговой аттестации в форме ЕГЭ Внешняя политика Александра I в 1801-1812 гг.
Внешняя политика Александра I в 1801-1812 гг. Основные ошибки при подаче документов на лицензирование
Основные ошибки при подаче документов на лицензирование Презентация на тему Изобразительное искусство классицизма и рококо
Презентация на тему Изобразительное искусство классицизма и рококо КИНЕШМА
КИНЕШМА Обработка нижнего среза изделия
Обработка нижнего среза изделия Педагогическая практика организации внеурочной и внеклассной деятельности
Педагогическая практика организации внеурочной и внеклассной деятельности Положение об общественном совете муниципального образования Северодвинск
Положение об общественном совете муниципального образования Северодвинск Луи , ПАСТЕР (Pasteur)
Луи , ПАСТЕР (Pasteur) Хохломская роспись
Хохломская роспись Горячая линия
Горячая линия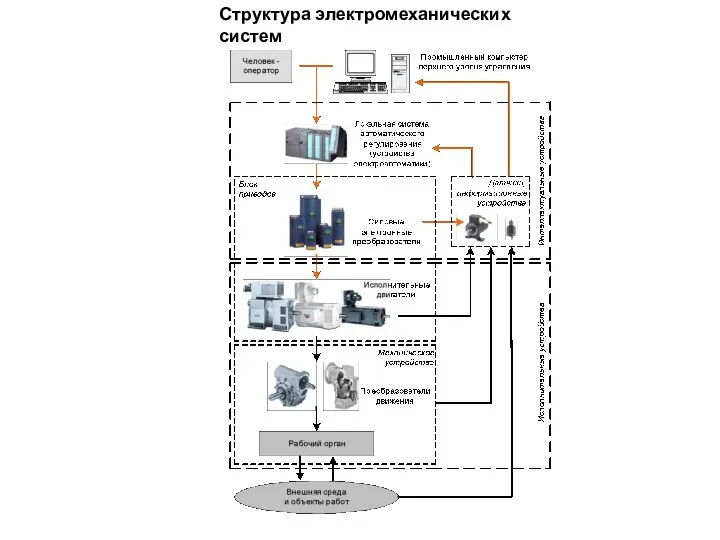 Структура электромеханических систем
Структура электромеханических систем Характер человека
Характер человека Преодоление сложностей при запоминании таблицы умножения
Преодоление сложностей при запоминании таблицы умножения Презентация на тему Юридическая клиника в кыргызско-российском славянском университете имени Бориса Ельцина
Презентация на тему Юридическая клиника в кыргызско-российском славянском университете имени Бориса Ельцина  Презентация на тему Военно-патриотическое воспитание
Презентация на тему Военно-патриотическое воспитание Обобщающий урок во 2 классе
Обобщающий урок во 2 классе Дистрибуция прессы в сети супермаркетов в России. Тенденции и перспективы развития.
Дистрибуция прессы в сети супермаркетов в России. Тенденции и перспективы развития. Использование 3D технологии в медицине
Использование 3D технологии в медицине Кружок робототехники
Кружок робототехники Война за независимость США
Война за независимость США Современная теория фотосинтеза
Современная теория фотосинтеза Программный комплекс «Карат» предназначен для создания в базе данных показателей любого типа, ручного ввода или автоматической п
Программный комплекс «Карат» предназначен для создания в базе данных показателей любого типа, ручного ввода или автоматической п Prezentacia_лекція_10-1_ТЕК (3)
Prezentacia_лекція_10-1_ТЕК (3)