Слайд 2Слуцкий Евгений Евгеньевич
Выдающийся российский математик, статистик и экономист. Родился 7 апреля 1880г.

C 1901 по 1902 год учился в Киевском университете, в связи с политической деятельностью был исключён из него в 1902 г. С 1902 по 1905 г. учился в Мюнхенском политехникуме на машиностроительном отделении.
Слайд 3Слуцкий Евгений Евгеньевич
После революции, осенью 1905 года вновь поступил на юридический факультет

Киевского университета, который окончил с золотой медалью. В 1913 году был приглашен на работу в Киевский коммерческий институт народного хозяйства. С 1926 года работал в Центральном статистическом управлении, в том же году переехал на постоянное место жительства в Москву. С 1939 года работал в Математическом институте АН СССР.
Слайд 4Уравнение Слуцкого
Уравнение, смысл которого состоит в том, что изменение спроса на некоторый

товар при повышении или снижении его цены складывается из влияния непосредственного изменения спроса и косвенного влияния в результате переключения спроса на другие товары. Данное уравнение показывает, что изменение в спросе на i-й товар при изменении цены j-го товара является результатом двух эффектов: эффекта замещения и эффекта дохода.
Слайд 5Уравнение Слуцкого
где — заданные уровни цен, дохода и полезности. Корректность последнего перехода

в уравнении Слуцкого объясняется леммой Шепарда.
Слайд 6Условие Слуцкого
Условие эргодичности случайного процесса:
Необходимым и достаточным условием эргодичности относительно среднего стационарного

случайного процесса с корреляционной функцией Rx является выполнение следующего равенства:





 Ты, человек, любя природу,Хоть иногда её жалей:В увеселительных походахНе растопчи её полей.В вокзальной сутолоке векаТы оценит
Ты, человек, любя природу,Хоть иногда её жалей:В увеселительных походахНе растопчи её полей.В вокзальной сутолоке векаТы оценит NXP semiconductors, Москва. Краткий обзор
NXP semiconductors, Москва. Краткий обзор Однофазный TIG-инвертор
Однофазный TIG-инвертор Індекси цін у будівництві
Індекси цін у будівництві Банки и банковская система РФ. Тест
Банки и банковская система РФ. Тест Прикладной Тайм-менеджмент для программистов
Прикладной Тайм-менеджмент для программистов ГПОУ Горловский автотранспортный техникум. ГОУВПО Донецкий национальный технический университет
ГПОУ Горловский автотранспортный техникум. ГОУВПО Донецкий национальный технический университет Кабинет министров
Кабинет министров Республиканский научно-исследовательский институт интеллектуальной собственности ул. Б.Якиманка, д. 38, г. Москва, 119049 тел./факс: +
Республиканский научно-исследовательский институт интеллектуальной собственности ул. Б.Якиманка, д. 38, г. Москва, 119049 тел./факс: + Доброволец на ЧС. Особенности психологической устойчивости личного состава. Способы подготовки
Доброволец на ЧС. Особенности психологической устойчивости личного состава. Способы подготовки Сессия Госконтроль 2.0: образ будущего
Сессия Госконтроль 2.0: образ будущего Презентация Microsoft PowerPoint
Презентация Microsoft PowerPoint Перпендикуляр и наклонные
Перпендикуляр и наклонные Однородные члены предложения
Однородные члены предложения Предмет, метод, источники и принципы Трудового права
Предмет, метод, источники и принципы Трудового права Поэты Ставрополья о родном крае и о природе родного края
Поэты Ставрополья о родном крае и о природе родного края Педагогический совет «Поиск путей совершенствования образовательной среды школы при введении федерального государственного обр
Педагогический совет «Поиск путей совершенствования образовательной среды школы при введении федерального государственного обр Обзор на персонажа
Обзор на персонажа ВКР: Действительный цикл машины МВВ6 - 1 -2
ВКР: Действительный цикл машины МВВ6 - 1 -2 15 февраля 1861 года родился швейцарский физик-метролог Шарль Эдуард Гильом (Гийом).
15 февраля 1861 года родился швейцарский физик-метролог Шарль Эдуард Гильом (Гийом). Правила наложения жгутов повязок и шин
Правила наложения жгутов повязок и шин Вальдорфская система образования
Вальдорфская система образования Social Ecology Sustainable Development
Social Ecology Sustainable Development  Ваш профессиональный маршрут
Ваш профессиональный маршрут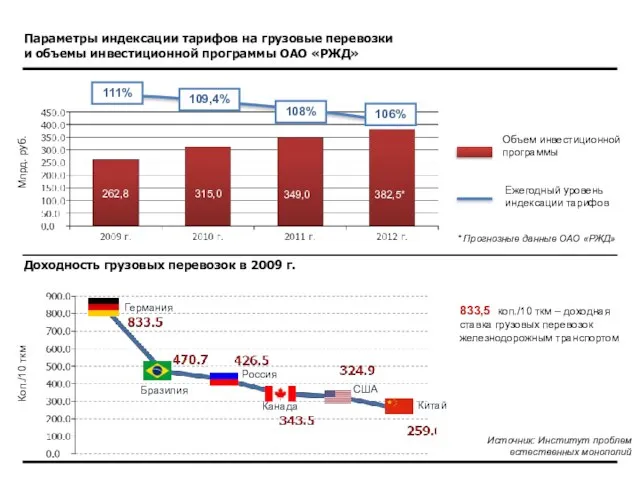 Параметры индексации тарифов на грузовые перевозки и объемы инвестиционной программы ОАО «РЖД»
Параметры индексации тарифов на грузовые перевозки и объемы инвестиционной программы ОАО «РЖД» Концепция воспитательной системы
Концепция воспитательной системы Технология создания и редактирования изображений в векторном редакторе
Технология создания и редактирования изображений в векторном редакторе Презентация на тему Использования краеведческого материала в образовательном процессе
Презентация на тему Использования краеведческого материала в образовательном процессе