Содержание
- 2. Цель: ввести понятие смежных и вертикальных углов, рассмотреть их свойства
- 3. Повторение: дерево знаний 1. Что такое луч? Как он обозначается? 2. Какая фигура называется углом? 3.
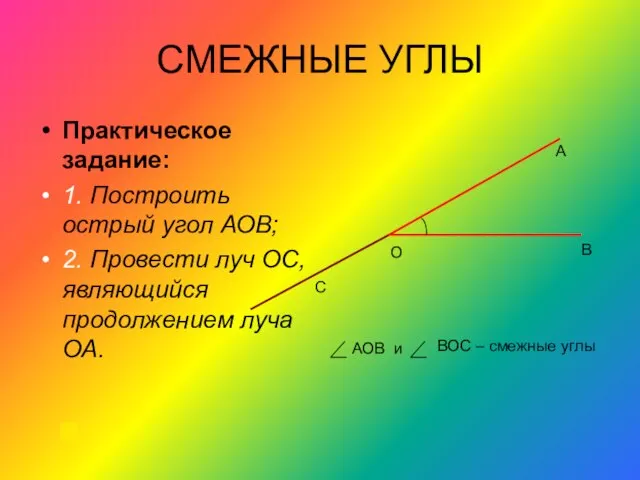
- 4. СМЕЖНЫЕ УГЛЫ Практическое задание: 1. Построить острый угол АОВ; 2. Провести луч ОС, являющийся продолжением луча
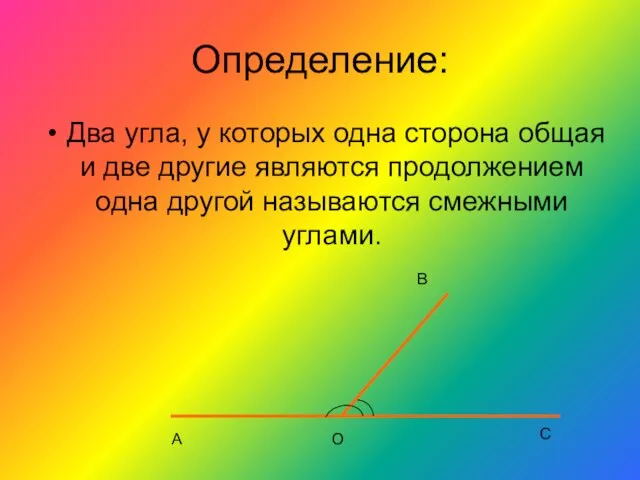
- 5. Определение: Два угла, у которых одна сторона общая и две другие являются продолжением одна другой называются
- 6. Свойство смежных углов 1. Какой угол АОВ? 2. Чему равна градусная мера угла? 3. На какие
- 7. ВЫВОД: АОВ+ Сумма смежных углов равна 180˚ ВОС =180˚
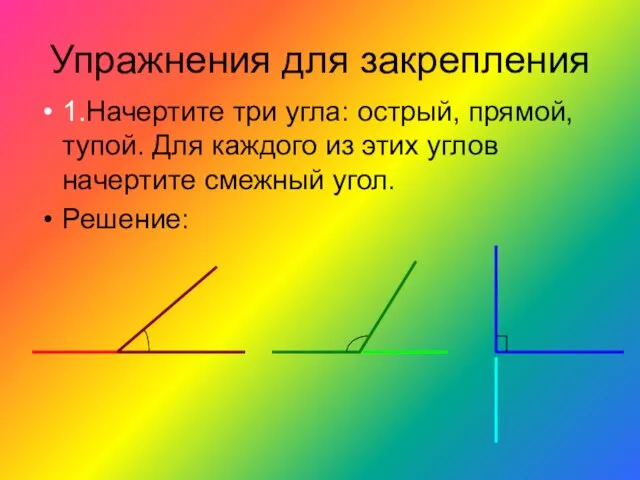
- 8. Упражнения для закрепления 1.Начертите три угла: острый, прямой, тупой. Для каждого из этих углов начертите смежный
- 9. 2. Один из смежных углов прямой. Каким (острым, прямым, тупым) является другой угол?
- 10. 3. Верно ли утверждение: если смежные углы равны, то они прямые? Рассуждай:
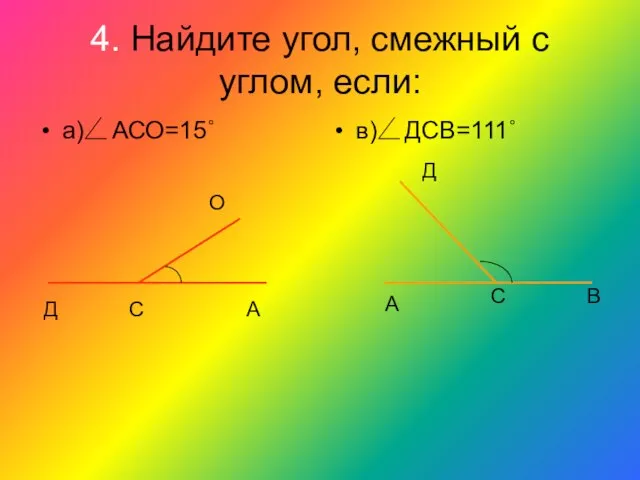
- 11. 4. Найдите угол, смежный с углом, если: а) АСО=15˚ в) ДСВ=111˚ Д С А О Д
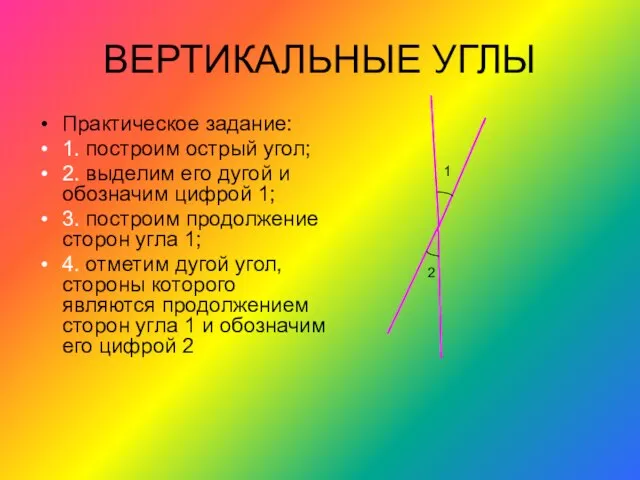
- 12. ВЕРТИКАЛЬНЫЕ УГЛЫ Практическое задание: 1. построим острый угол; 2. выделим его дугой и обозначим цифрой 1;
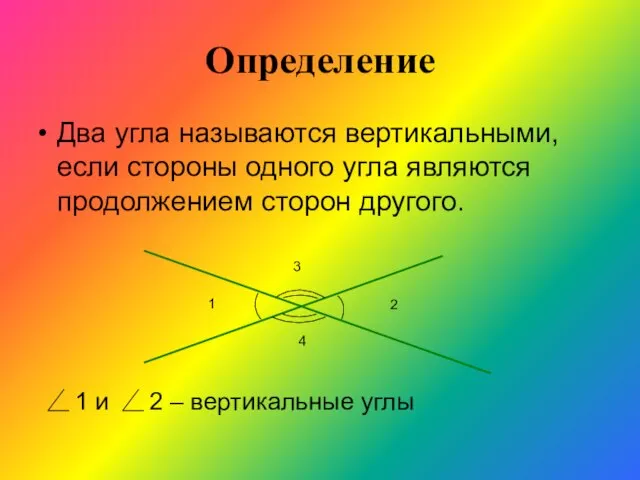
- 13. Определение Два угла называются вертикальными, если стороны одного угла являются продолжением сторон другого. 1 2 3
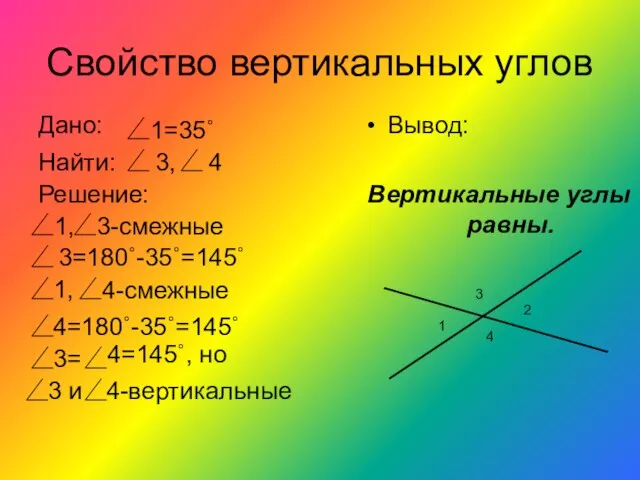
- 14. Свойство вертикальных углов Вывод: Вертикальные углы равны. 1 2 3 4 1=35˚ Найти: Дано: 3, 4
- 15. Упражнения для закрепления 1. При пересечении двух прямых а и в сумма каких-то углов равна 60˚.
- 16. №64(1) 1 3 2 4 Дано: 2=117˚ Найти: 1, 3, 4. Решение: 1=180˚- 2=180˚-117˚= =63˚- cв-во
- 17. Самостоятельная работа I вариант II вариант а b 45º m n 110º При пересечении двух прямых
- 19. Скачать презентацию







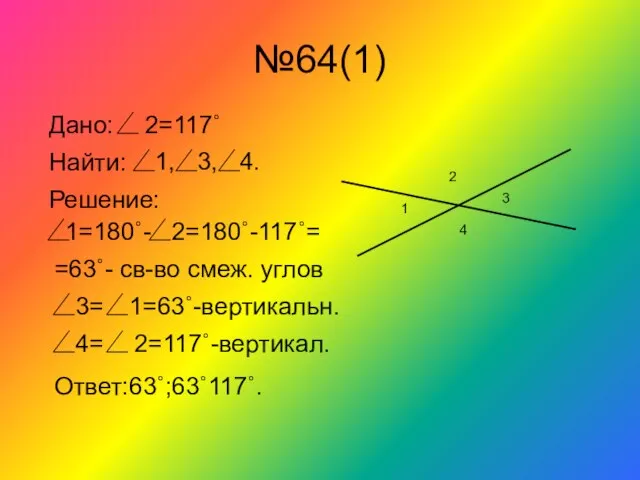
 Мезенская роспись
Мезенская роспись Презентация на тему Урок по роману А.С. Пушкина «Капитанская дочка» (глава XI «Мятежная слобода»)
Презентация на тему Урок по роману А.С. Пушкина «Капитанская дочка» (глава XI «Мятежная слобода»)  Быстрый путьот стартапа до бизнеса
Быстрый путьот стартапа до бизнеса Тема урока: «Сложное предложение. Общая характеристика сложного предложения».
Тема урока: «Сложное предложение. Общая характеристика сложного предложения». Презентация на тему Три состояния вещества Физика 7 класс
Презентация на тему Три состояния вещества Физика 7 класс  Сложные вещества. Бинарные соединения. 8 класс
Сложные вещества. Бинарные соединения. 8 класс Рабочие документы аудитора
Рабочие документы аудитора 1
1 Воскресная прогулка к храму иконы Божьей матери «Иверской»
Воскресная прогулка к храму иконы Божьей матери «Иверской» История создания произведения «Капитанская дочка»
История создания произведения «Капитанская дочка» Понятие культура труда. Профессиональное самоопределение и карьера
Понятие культура труда. Профессиональное самоопределение и карьера Публичный ежегодный доклад директора МОУ«Гимназия имени Подольских курсантов» Муниной В.Н.за 2009 – 2010 учебный год
Публичный ежегодный доклад директора МОУ«Гимназия имени Подольских курсантов» Муниной В.Н.за 2009 – 2010 учебный год Диваны 2019 года
Диваны 2019 года Презентация на тему Народы Африки
Презентация на тему Народы Африки  Язык жестов
Язык жестов АПАРТРИНГ. Центр обеспечения недвижимости
АПАРТРИНГ. Центр обеспечения недвижимости Чрезвычайные ситуации техногенного характера
Чрезвычайные ситуации техногенного характера Буратино
Буратино Знакомство с лабораторным оборудованием. Приемы нагревания
Знакомство с лабораторным оборудованием. Приемы нагревания Вид на Аппиеву дорогу, самая значимая из античных общественных дорог Рима. Дорога, проложенная в 312 году до н. э. при цензоре Аппии Кл
Вид на Аппиеву дорогу, самая значимая из античных общественных дорог Рима. Дорога, проложенная в 312 году до н. э. при цензоре Аппии Кл Электролитическая диссоциация (8 класс)
Электролитическая диссоциация (8 класс) Культура отдыха
Культура отдыха Президент школьного ученического самоуправления Совет гимназистов
Президент школьного ученического самоуправления Совет гимназистов Модели
Модели 20140110_urok_3
20140110_urok_3 Косметический B2B маркетплейс для вашего бизнеса Beauty2B:
Косметический B2B маркетплейс для вашего бизнеса Beauty2B: Существующие механизмы и инструменты для обмена опытом и помощи в поиске европейских партнеров
Существующие механизмы и инструменты для обмена опытом и помощи в поиске европейских партнеров Презентация на тему Памятники животным презентация
Презентация на тему Памятники животным презентация