Содержание
- 2. линзы, преобразующие параллельный пучок световых лучей в сходящийся: Собирающие линзы двояковыпуклые плоско-выпуклые выпукло-вогнутые
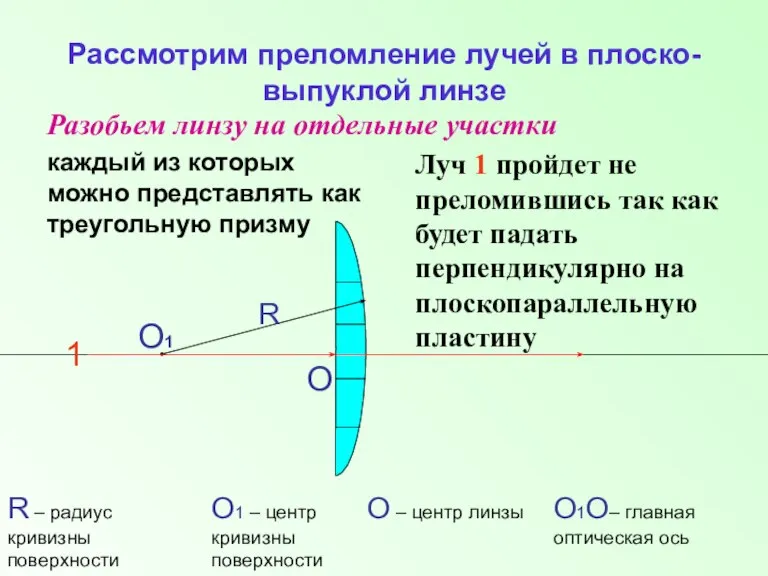
- 3. Рассмотрим преломление лучей в плоско-выпуклой линзе Разобьем линзу на отдельные участки каждый из которых можно представлять
- 4. Рассмотрим преломление лучей в плоско-выпуклой линзе О R 2 1 Луч 2 падая на вторую границу
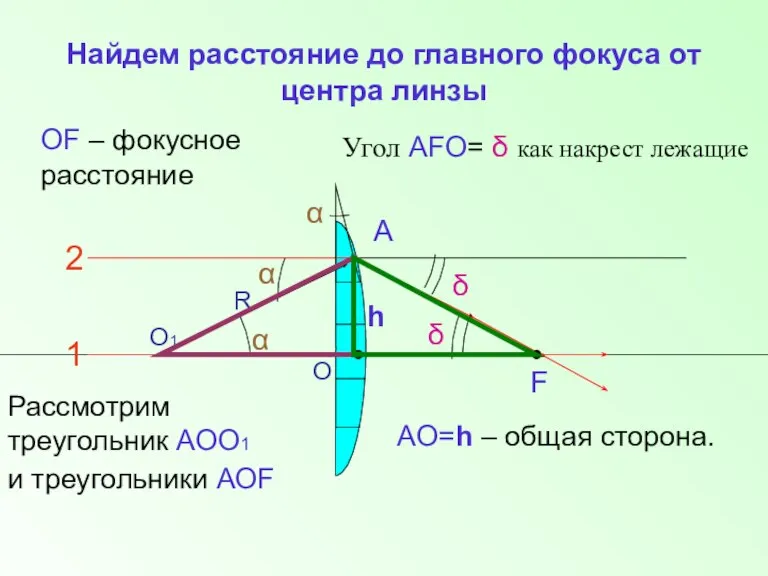
- 5. Найдем расстояние до главного фокуса от центра линзы О1 R 2 1 α F δ О
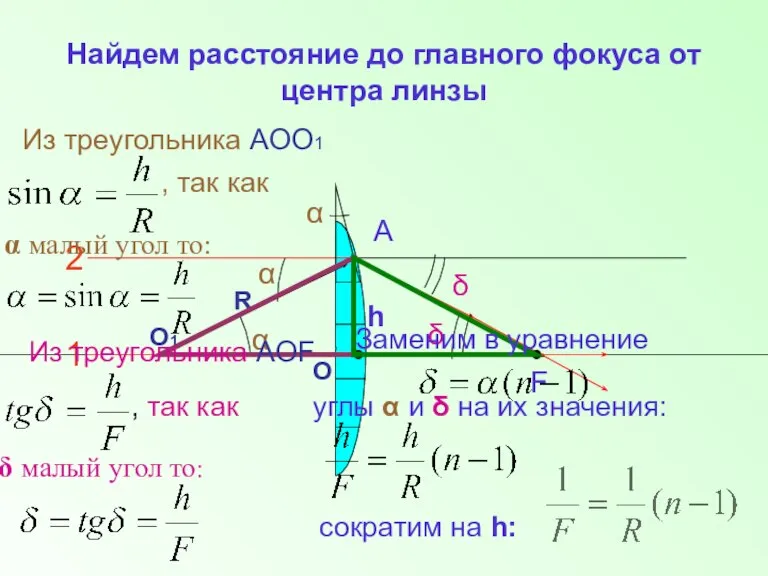
- 6. Найдем расстояние до главного фокуса от центра линзы Из треугольника АОО1 , так как α малый
- 7. двояковыпуклые выпукло-вогнутые Любую собирающую линзу можно рассматривать как совокупность двух плоско-выпуклые линз. O2 Преломление лучей будет
- 8. Оптическая сила линзы - физическая величина, обратная фокусному расстоянию. Диоптрия - оптическая сила линзы с фокусным
- 9. Для собирающих линз двояковыпуклые плоско-выпуклые выпукло-вогнутые ,так как R1>0 R2>0 ,так как R>0 ,так как |R2|>R1
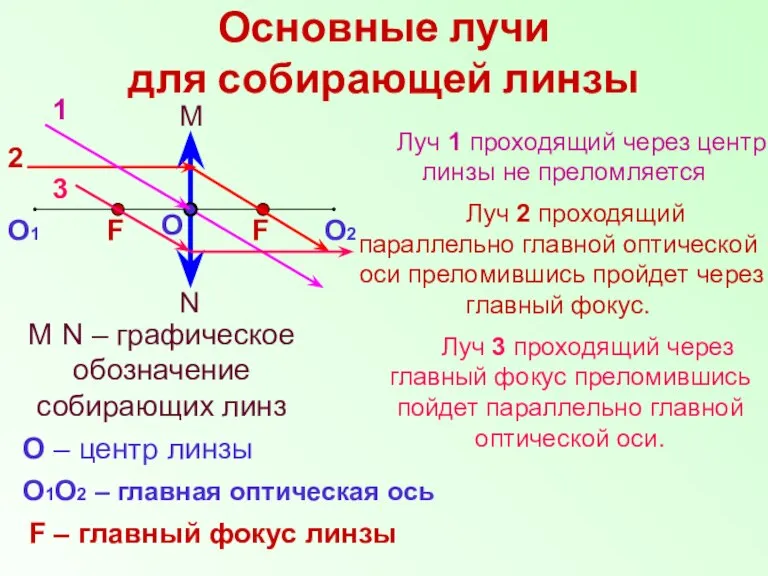
- 10. Основные лучи для собирающей линзы N M M N – графическое обозначение собирающих линз О О
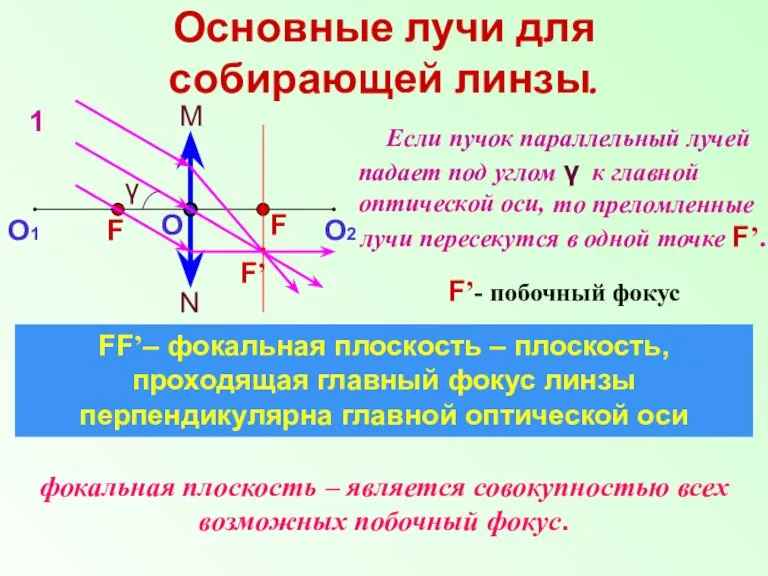
- 11. Основные лучи для собирающей линзы. N M О О1 О2 F F FF’– фокальная плоскость –
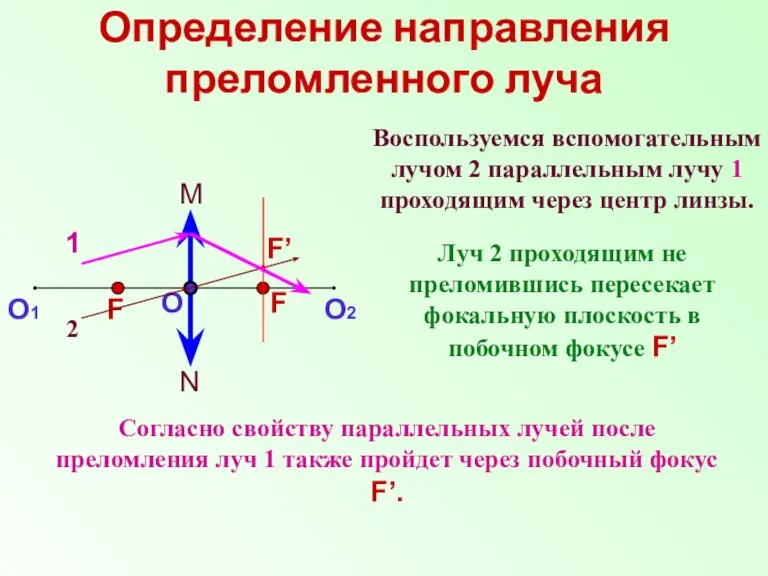
- 12. Определение направления преломленного луча Воспользуемся вспомогательным лучом 2 параллельным лучу 1 проходящим через центр линзы. 1
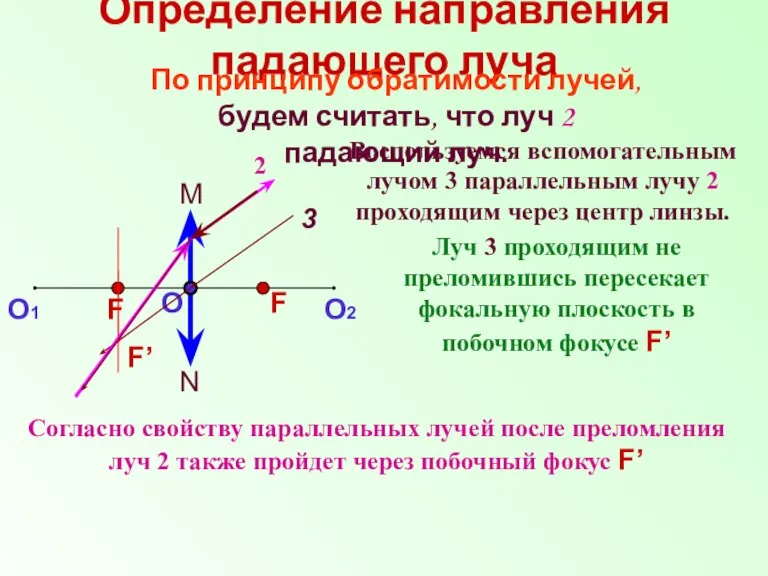
- 13. Определение направления падающего луча 3 2 Луч 3 проходящим не преломившись пересекает фокальную плоскость в побочном
- 15. Скачать презентацию





 Global Trading St. Petersburg
Global Trading St. Petersburg Развитие отечественного производства кремниевых СБИС
Развитие отечественного производства кремниевых СБИС Дроид-игрушка Sphero BB-9E
Дроид-игрушка Sphero BB-9E Презентация магистерской диссертации по специальности «Юриспруденция»
Презентация магистерской диссертации по специальности «Юриспруденция» Технологии обучения
Технологии обучения Консервирование плодов и ягод
Консервирование плодов и ягод Урок русского языка в 5 классе«Мой учебник»
Урок русского языка в 5 классе«Мой учебник» Астрология и ее роль в жизни человека
Астрология и ее роль в жизни человека Презентация на тему Электромагнитные волны
Презентация на тему Электромагнитные волны О ходе реализации в Сибирском федеральном округе постановления Правительства Российской Федерации от 31 мая 2011 г. № 436
О ходе реализации в Сибирском федеральном округе постановления Правительства Российской Федерации от 31 мая 2011 г. № 436 Межкультурные взаимодействия
Межкультурные взаимодействия Предоплаты и начисления, денежные средства и обязательства
Предоплаты и начисления, денежные средства и обязательства Улучшение жилищных условий населения муниципального образования город Нягань
Улучшение жилищных условий населения муниципального образования город Нягань Особенности проведения государственной (итоговой) аттестации выпускников общеобразовательных учреждений в 2012 году
Особенности проведения государственной (итоговой) аттестации выпускников общеобразовательных учреждений в 2012 году Отопление. Назначение отопления
Отопление. Назначение отопления Legacy kanal RSO - привлечение внимания людей к прошлому наших народов
Legacy kanal RSO - привлечение внимания людей к прошлому наших народов ABC (A-I)
ABC (A-I) Choosing a profession
Choosing a profession Витамины в нашей пище
Витамины в нашей пище Россия - наша Родина
Россия - наша Родина Итоги реализации «Основных направлений развития школы» МОУ СОШ №92
Итоги реализации «Основных направлений развития школы» МОУ СОШ №92 Зеркало времени. Технология 3 класс
Зеркало времени. Технология 3 класс Горлачев Никита Алексеевич
Горлачев Никита Алексеевич Выбираем эффективную диету. Калькулятор калорий + персональное меню.
Выбираем эффективную диету. Калькулятор калорий + персональное меню. Наш портфель
Наш портфель Курс молодого преподавателя, или будни Bonifacy в Вышке
Курс молодого преподавателя, или будни Bonifacy в Вышке Технический центр «АТТ-авто» предлагает сотрудничество в области ремонта автомобилей
Технический центр «АТТ-авто» предлагает сотрудничество в области ремонта автомобилей Анализ конкурентов медиа-проекта Между нами
Анализ конкурентов медиа-проекта Между нами