Современная криптография

Типы шифрования
Симметричное
Асимметричное

Симметричное шифрование
Ключ шифрования равен ключу расшифровки
Самые древние виды шифрования относятся к этому типу
Самые известные представители – AES, DES, RC4
Для секретного ключа K
Encrypt(M,K) = C
Decrypt(C,K) = M

Применения симметричного шифрования
Быстрое шифрование данных
Возможность потокового шифрования

Асимметричное шифрование
Ключ шифрования НЕ равен ключу расшифровки
Изобретен 40 лет назад
Самые известные представители – RSA, ECC
Для секретной пары ключей K и K’
Encrypt(M,K) = C
Decrypt(C,K’) = M
K’!=K

Применения асимметричного шифрования
Обмен ключами симметричного шифрования
Проверка подлинности

Блочные шифры
Шифруют блоками постоянного размера
Все асимметричные шифры относятся к блочным
Популярные симметричные – тоже (AES, DES)
Идеальный блочный шифр являет собой шифр подстановки, заменяющий один блок текста на другой, причем взаимосвязь полностью задается ключом, однако восстановить по ней ключ невозможно

Потоковые шифры
Генерируют ключевой поток
Позволяют шифровать буквально по одному биту
Шифрование часто совпадает с расшифровкой
Операция шифрования обычно выглядит как
???????? – ключевой поток
⊕ – XOR (побитовое сложение по модулю 2)
MESSAGE – исходное сообщение
_____________
CIPHERTEXT – зашифрованное сообщение

AES, DES и компания
Какая-то аццкая муть, является предметом изучения математиков, можно наблюдать на NSUCRYPTO, например.

Режим связывания блоков
Атаки, как правило, вообще можно осуществлять на любой блочный шифр, даже идеальный
И главное, совершенно не нужно разбираться как оно работает
Создан чтобы избежать поблочного анализа
Очевидно, что для каждого блока X для таблицы подстановки S
S(X1) == S(X2) тогда и только тогда когда X1==X2
Это беда

Режим связывания блоков
ECB
CBC
PLAIN

Режим связывания блоков
В режиме CBC для шифрования:
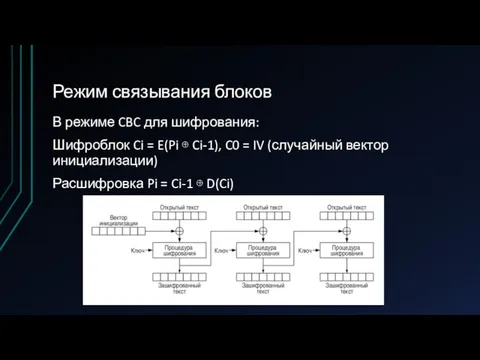
Шифроблок Ci = E(Pi ⊕ Ci-1), C0 = IV (случайный вектор инициализации)
Расшифровка Pi = Ci-1 ⊕ D(Ci)

Режим связывания блоков
Напрямую из процедуры расшифровки получаем
Если Pi = Ci-1 ⊕ D(Ci) то заменяя Ci-1 мы заменяем Pi
То есть если нам известен некоторый текст скрытый за шифрованием, мы можем создать ЛЮБОЙ текст такой же длины как Pevil = Cevil ⊕ D(Ci), Cevil = Pi ⊕ Ci-1 ⊕ EVILTEXT
Вывод:
Симметричная криптография хреново подходит для проверки подлинности (еще бы)

RSA

Как накосячить с модулем RSA
Использовать небольшое N (привет NSUCRYPTO)
Использовать N такое где |p-q| мало, тогда применяется алгоритм факторизации Ферма
Использовать N где p-1 имеет малые делители (гладкое) – применяется p-1 метод Полларда
Использовать N где p+1 имеет малые делители – метод p+1 Уильямса
Слить информацию о части бит p или q – Coppersmith method или “factoring with a hint” в CrypTool

Как накосячить RSA (ещё)

Как накосячить RSA (и ещё)
Не проверять подлинность N при обмене ключами. Тогда можно осуществить атаку “человек посередине” подменив N своим и расшифровывая-зашифровывая данные прозрачно для двух собеседников. Но это в CTF уже экзотика.

Секундочку, но ведь RSA шифрует числа?
Ага, есть такое дело.
Чтобы перевести строку в число достаточно просто взять составляющие ее байты и посчитать их байтами числа.
В языке Python это делается как int(‘stroka’.encode(‘hex’),16)
В обратную сторону hex(num)[2:].replace(‘L’,’’).decode(‘hex’)

Полезные инструменты
Python, без него здесь почти никак
Libnum, позволяет выполнять разные математические операции, близкие к CTF. Или gmpy/gmpy2 (как более общее решение).
Sagemath, для отчаянных. Обладает огромным списком возможностей, но странноват, большой и тормозит.
Google + site:github.com для поиска готовых скриптов
GIMP – позволяет открывать байты (расширение .data) как картинку, очень полезный инструмент для поверхностного анализа данных (энтропия “на глазок”)
Xortool, позволяет выполнять операцию xor над файлами