Содержание
- 2. План Спектральный анализ Мощность сигнала, теорема Парсеваля Спектрограммы, усреднение во времени Частотно-временное разрешение Быстрая свертка Свертка
- 3. Мощность и амплитуда Мощность пропорциональна квадрату амплитуды RMS (среднеквадратичное зачение) сигнала: Окна при вычислении RMS Вычисление
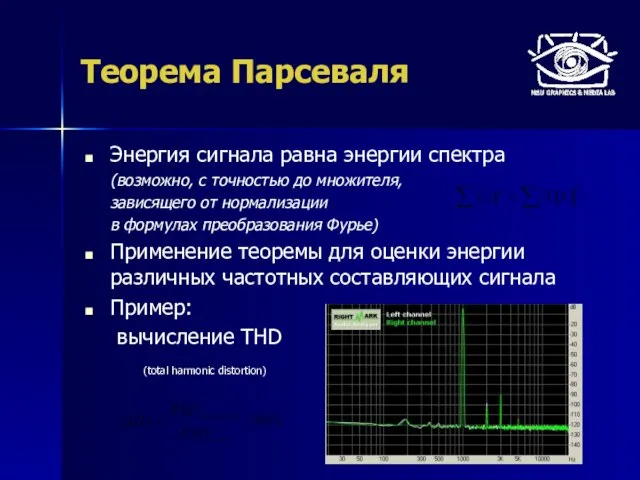
- 4. Теорема Парсеваля Энергия сигнала равна энергии спектра (возможно, с точностью до множителя, зависящего от нормализации в
- 5. Спектральный анализ Как вычислить и отобразить спектр сигнала? Взять нужный отрезок сигнала длины 2m; если нужный
- 6. Свойства ДПФ Линейность Комплексное ДПФ от вещественного сигнала обладает симметрией относительно коэффициента k = N/2. Таким
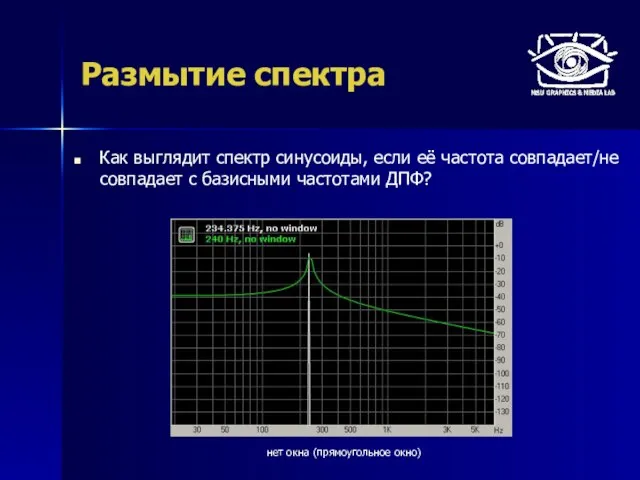
- 7. Размытие спектра Как выглядит спектр синусоиды, если её частота совпадает/не совпадает с базисными частотами ДПФ? нет
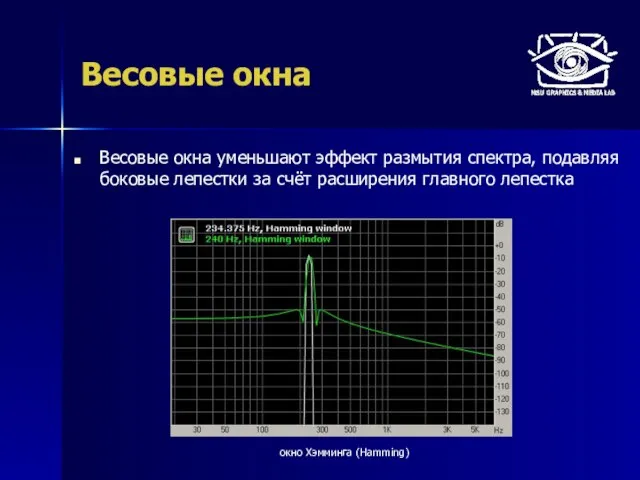
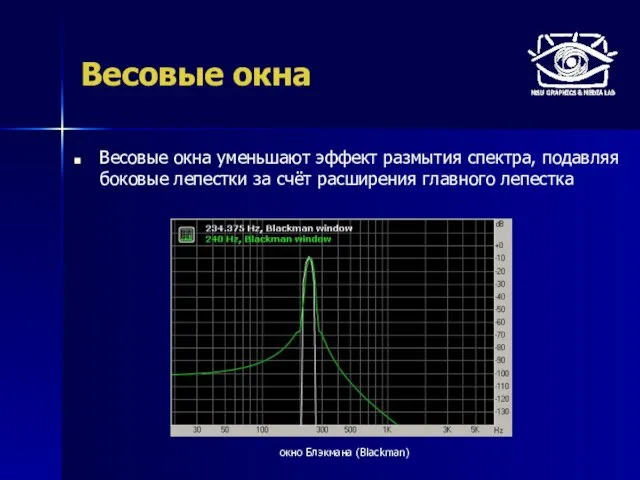
- 8. Весовые окна Весовые окна уменьшают эффект размытия спектра, подавляя боковые лепестки за счёт расширения главного лепестка
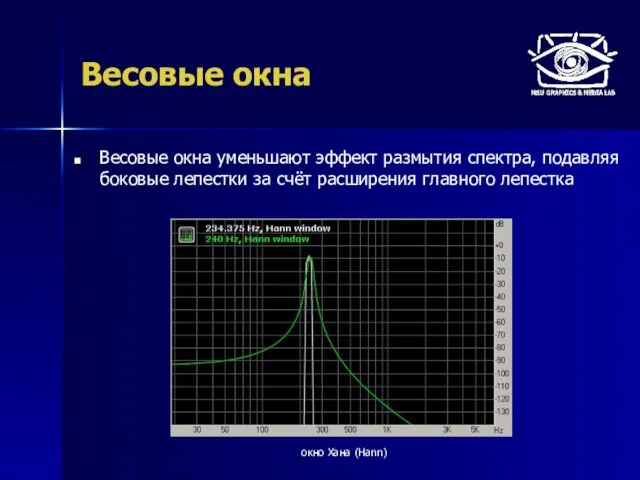
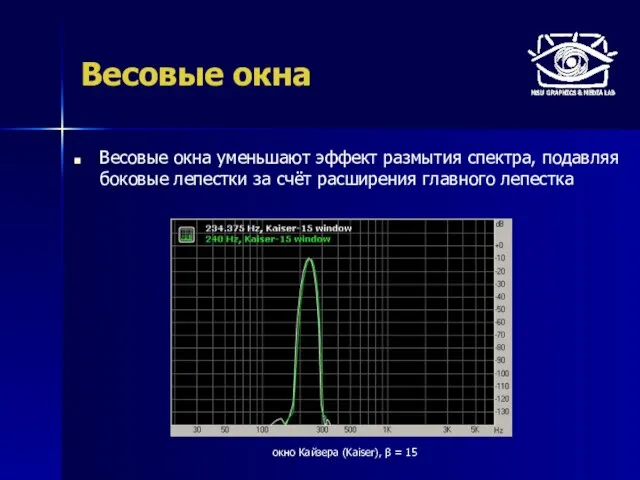
- 9. Весовые окна Весовые окна уменьшают эффект размытия спектра, подавляя боковые лепестки за счёт расширения главного лепестка
- 10. Весовые окна Весовые окна уменьшают эффект размытия спектра, подавляя боковые лепестки за счёт расширения главного лепестка
- 11. Весовые окна Весовые окна уменьшают эффект размытия спектра, подавляя боковые лепестки за счёт расширения главного лепестка
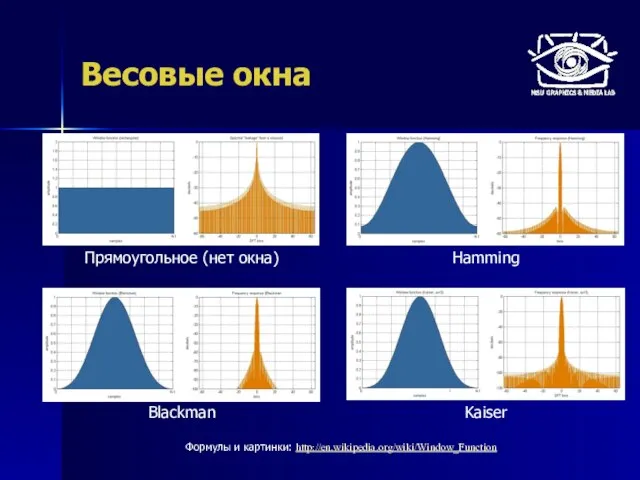
- 12. Весовые окна Прямоугольное (нет окна) Hamming Blackman Kaiser Формулы и картинки: http://en.wikipedia.org/wiki/Window_Function
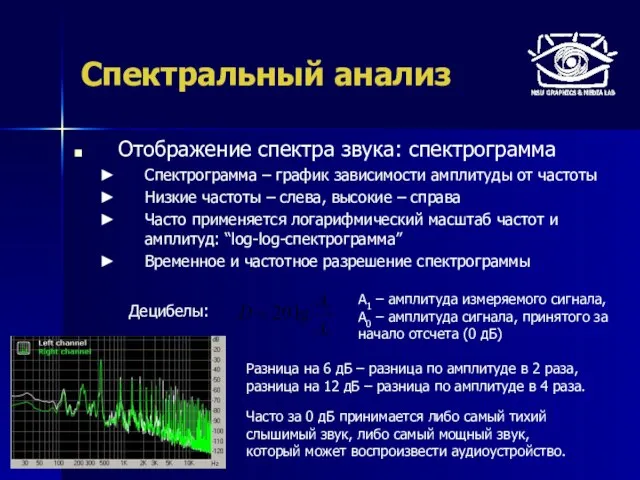
- 13. Спектральный анализ Отображение спектра звука: спектрограмма Спектрограмма – график зависимости амплитуды от частоты Низкие частоты –
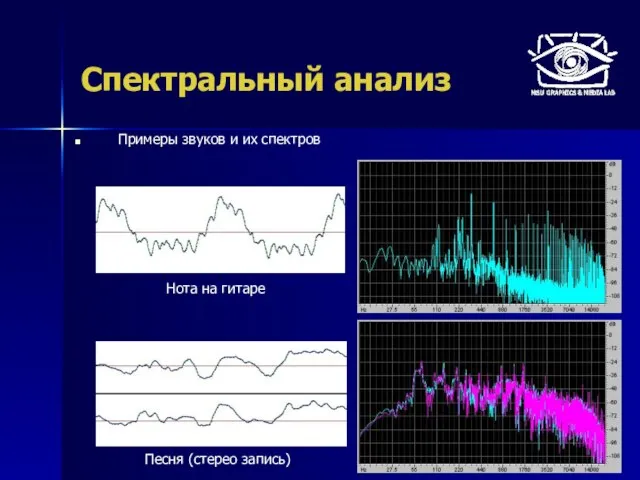
- 14. Спектральный анализ Примеры звуков и их спектров Песня (стерео запись) Нота на гитаре
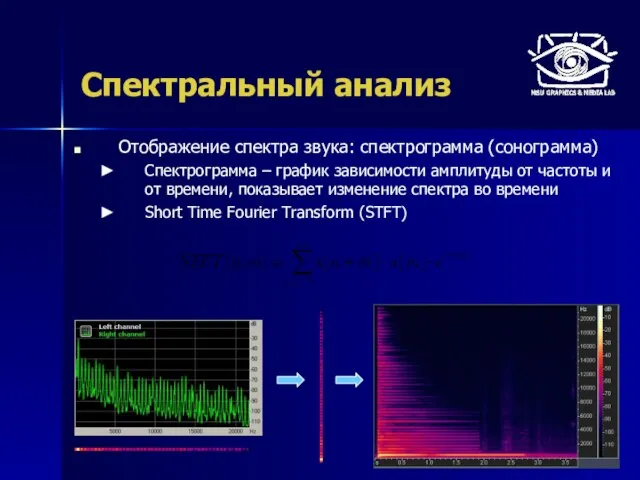
- 15. Спектральный анализ Отображение спектра звука: спектрограмма (сонограмма) Спектрограмма – график зависимости амплитуды от частоты и от
- 16. Спектральный анализ Отображение спектра звука: спектрограмма (сонограмма) Спектрограмма – график зависимости амплитуды от частоты и от
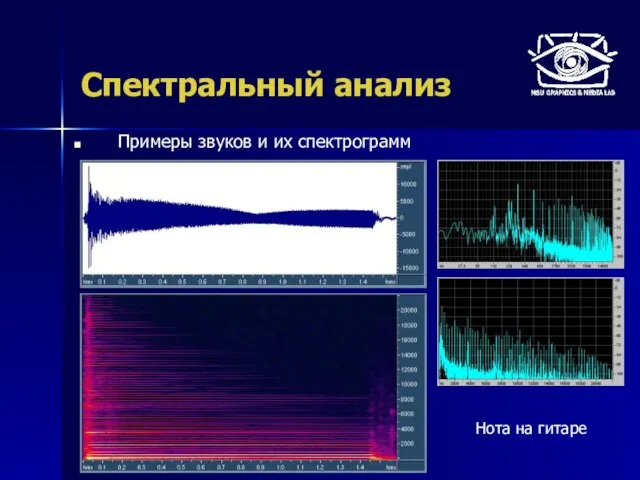
- 17. Спектральный анализ Примеры звуков и их спектрограмм Нота на гитаре
- 18. Спектральный анализ Спектрограммы шума Типы шумов: белый (постоянная PSD), розовый (3 дБ/окт.), коричневый (6 дБ/окт.) Вариация
- 19. Построение спектрограмм Мел-шкала частот Недостаточное частотное разрешение на НЧ, недостаточное временное разрешение на ВЧ Обычная спектрограмма,
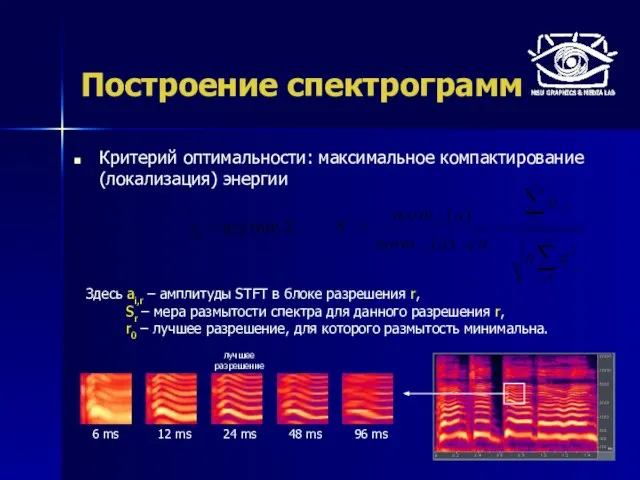
- 20. Построение спектрограмм Адаптивное частотно-временное разрешение спектрограмм Критерий оптимальности: максимально компактная локализация энергии (минимальное размытие спектрограммы) Адаптивная
- 21. Построение спектрограмм Критерий оптимальности: максимальное компактирование (локализация) энергии 6 ms 12 ms 24 ms 48 ms
- 22. Свертка и фильтрация Основные термины Свертка (convolution), фильтрация (filtering) Фильтр (filter), ядро фильтра (kernel) Импульсная, частотная
- 23. Быстрая свертка Прямое вычисление: M·N умножений (M – размер ядра свертки, N – длина сигнала) Теорема
- 24. Быстрая свертка Как изменяется длина сигнала при свертке? Она увеличивается на длину ядра минус 1 (т.к.
- 25. Вычисление свертки Быстрая свертка через FFT Неоптимальна по скорости, когда длины сигнала и ядра сильно различаются
- 26. Разбиение ядра Проблема секционной свертки: сигнал надо накапливать блоками, сравнимыми по размеру с длиной ядра свертки
- 27. Частотная характеристика Получение частотной характеристики по ядру Дополнение нулями FFT Берем модули комплексных коэффициентов Свертка =
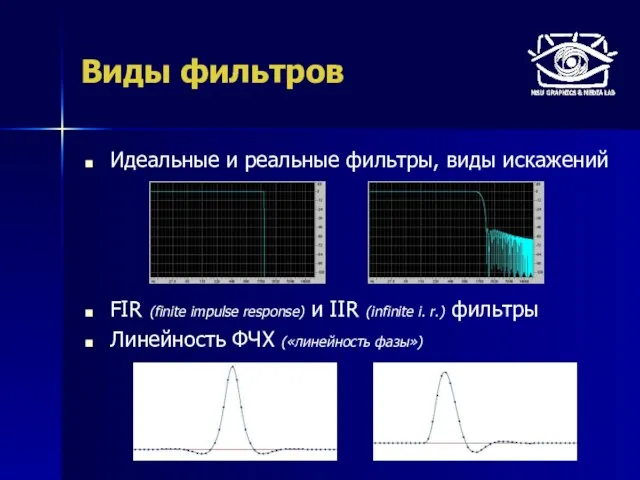
- 28. Виды фильтров Идеальные и реальные фильтры, виды искажений FIR (finite impulse response) и IIR (infinite i.
- 29. Построение фильтров Простейший НЧ-фильтр – windowed sinc Метод спектральной инверсии* Вычитание фильтра из единичного импульса –
- 30. Построение фильтров Метод весового окна Построение фильтра с линейной фазой по произвольной заданной частотной характеристике Частотная
- 31. Построение фильтров Метод весового окна (идея метода – взять обратное FFT от требуемой АЧХ) Дана требуемая
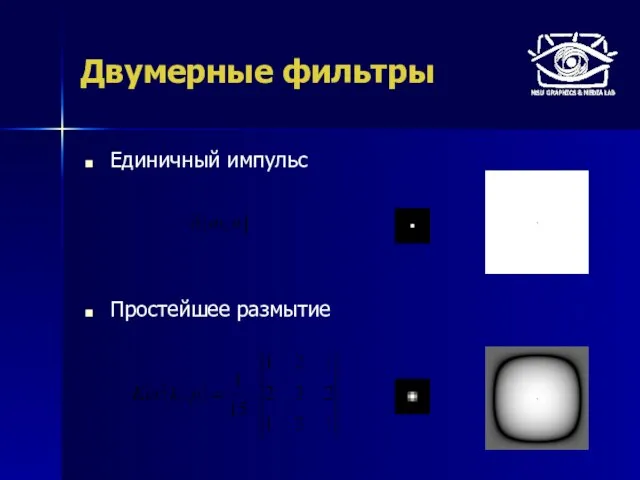
- 32. Единичный импульс Простейшее размытие Двумерные фильтры
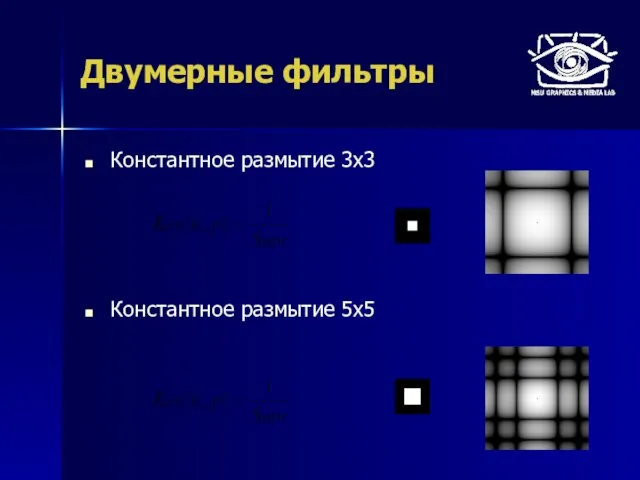
- 33. Константное размытие 3х3 Константное размытие 5х5 Двумерные фильтры
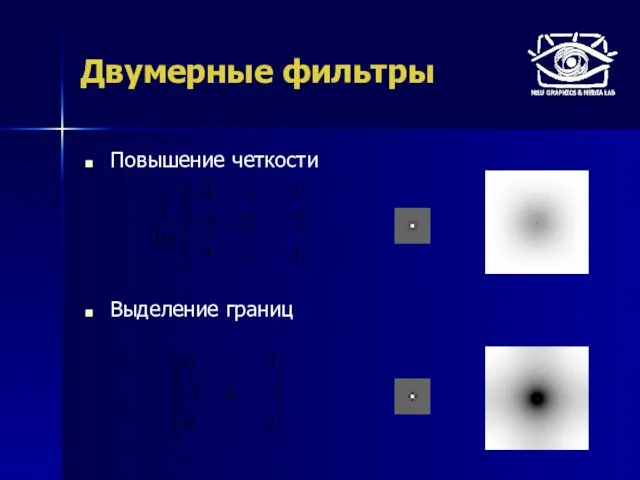
- 34. Повышение четкости Выделение границ Двумерные фильтры
- 35. Тиснение Пример спектра изображения Двумерные фильтры
- 36. Эквалайзеры Эквалайзер – устройство коррекции тембра сигнала, изменяющее амплитуды его частотных составляющих Изначально применялись для выравнивания
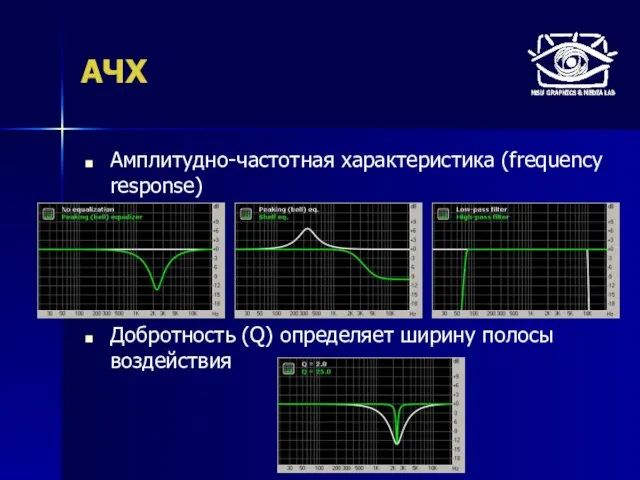
- 37. АЧХ Амплитудно-частотная характеристика (frequency response) Добротность (Q) определяет ширину полосы воздействия
- 38. Виды эквалайзеров По управлению АЧХ: Параметрические: можно выбирать одну из имеющихся форм АЧХ и задавать ее
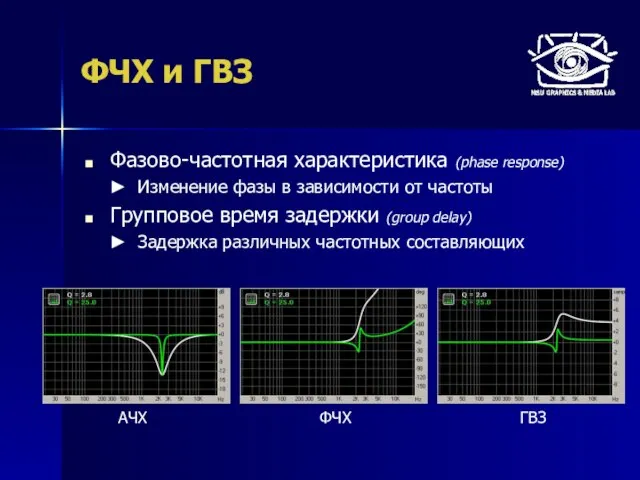
- 39. ФЧХ и ГВЗ Фазово-частотная характеристика (phase response) Изменение фазы в зависимости от частоты Групповое время задержки
- 40. Импульсная характеристика Конечная (FIR) Легко достичь линейной ФЧХ Бесконечная (IIR) Нелинейная ФЧХ Звон фильтров (ringing) Линейная
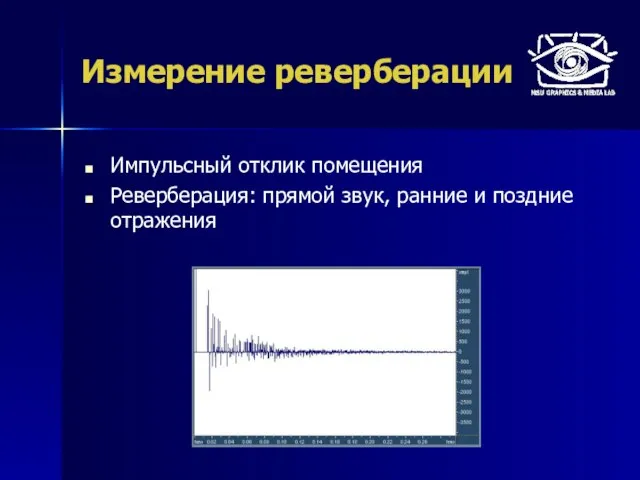
- 41. Измерение реверберации Импульсный отклик помещения Реверберация: прямой звук, ранние и поздние отражения
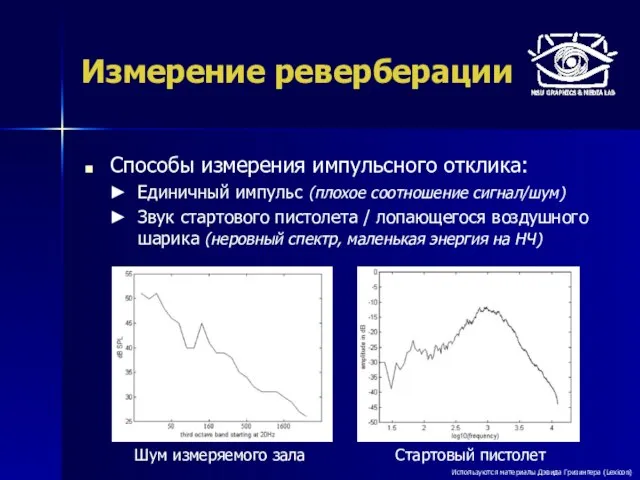
- 42. Измерение реверберации Способы измерения импульсного отклика: Единичный импульс (плохое соотношение сигнал/шум) Звук стартового пистолета / лопающегося
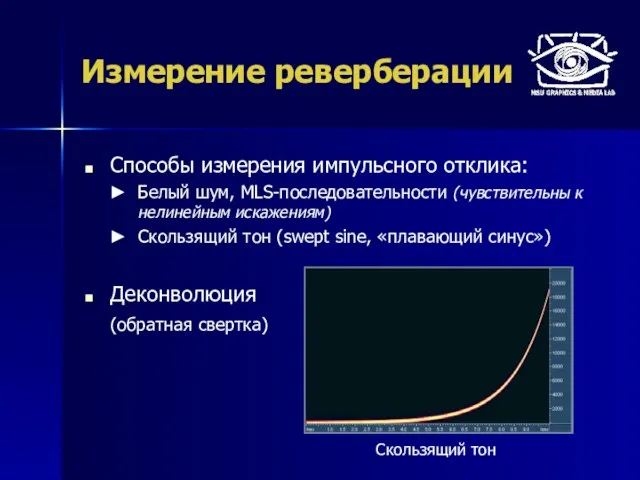
- 43. Измерение реверберации Способы измерения импульсного отклика: Белый шум, MLS-последовательности (чувствительны к нелинейным искажениям) Скользящий тон (swept
- 45. Скачать презентацию





















 HIPAK Kinetic 2400 AF / 2600 AF
HIPAK Kinetic 2400 AF / 2600 AF Прыжок в длину с места
Прыжок в длину с места МКОУ «Приреченская основная общеобразовательная школа Верхнемамонского муниципального района Воронежской области»ЛАГЕРЬ С
МКОУ «Приреченская основная общеобразовательная школа Верхнемамонского муниципального района Воронежской области»ЛАГЕРЬ С  Презентация без названия
Презентация без названия Disaster
Disaster Экзаменационный стресс
Экзаменационный стресс 1
1 Святой праведный старец Феодор Томский
Святой праведный старец Феодор Томский Современное потребление
Современное потребление  Изменение экономической конъюнктуры и эволюция маркетинговых концепций на примере ВТБ24
Изменение экономической конъюнктуры и эволюция маркетинговых концепций на примере ВТБ24 Характер философского знания и задачи философии
Характер философского знания и задачи философии Агентство Соединенных Штатов по Международному Развитию Винрок Интернэшнл
Агентство Соединенных Штатов по Международному Развитию Винрок Интернэшнл Источники права в Грузии
Источники права в Грузии Презентация кабинета химии
Презентация кабинета химии 5 ПСХЭ символы
5 ПСХЭ символы Ослабление влияния помех на аудиоаппаратуру сетевыми фильтрами
Ослабление влияния помех на аудиоаппаратуру сетевыми фильтрами Презентация на тему Отряд Вши
Презентация на тему Отряд Вши  Круглый стол «Социальная активность молодежи в реальном и виртуальном социальном пространстве».
Круглый стол «Социальная активность молодежи в реальном и виртуальном социальном пространстве». Эффект лотоса
Эффект лотоса Гибридизация
Гибридизация Паукообразные 2 класс
Паукообразные 2 класс Нагрузочное тестирование Описание услуг
Нагрузочное тестирование Описание услуг Проектная деятельность
Проектная деятельность Презентация на тему Буллинг
Презентация на тему Буллинг Happy Holidays
Happy Holidays Нейропсихология продаж
Нейропсихология продаж Презентация на тему Как жили на Руси
Презентация на тему Как жили на Руси Вирусы и антивирусы
Вирусы и антивирусы