Содержание
- 2. Способы решения квадратных уравнений Нахождение корней неполных квадратных уравнений Нахождение корней уравнения по формуле Нахождение корней
- 3. Неполные квадратные уравнения ax2 = 0 x2 = 0 x1 = x2 = 0 Пример Пример
- 4. Нахождение дискриминанта 2. Определение количества корней квадратного уравнения и их нахождение, в зависимости от значения D
- 5. Формула II (коэффициент b - четный) 1. Нахождение дискриминанта 2. Определение количества корней квадратного уравнения и
- 6. Обратная теорема Виета Если числа m и n таковы, что их сумма равна –р, а их
- 7. Если a + b + c = 0, то х1 = 1, х2 = Пример: 2х2
- 8. Решение уравнений по формуле I сам. работа Ответ:
- 9. Решение уравнений по формуле I сам. работа Ответ: 6
- 10. Решение уравнений по формуле I Ответ: нет корней сам. работа
- 11. Решение уравнений по формуле II сам. работа Ответ: -8; 6
- 12. сам. работа Решение неполных квадратных уравнений (с = 0) 5х2 – 12х = 0 х(5х –
- 13. сам. работа Решение неполных квадратных уравнений (b = 0) 9х2 – 16 = 0, 9х2 =
- 15. Скачать презентацию












 Конкурс «Анимация и Образование»
Конкурс «Анимация и Образование» Приказ о требованиях к плану финансово-хозяйственной деятельности государственного (муниципального) учреждения
Приказ о требованиях к плану финансово-хозяйственной деятельности государственного (муниципального) учреждения селекция
селекция Индивидуальное задание к лабораторной работе №3. Приворотные кексы
Индивидуальное задание к лабораторной работе №3. Приворотные кексы 1520 Стратегическое Партнерство Финансово-инвестиционная политика национальных железнодорожных компаний в условиях посткризисно
1520 Стратегическое Партнерство Финансово-инвестиционная политика национальных железнодорожных компаний в условиях посткризисно Кутузов и Наполеон в романе Л.Н. Толстого «Война и мир»
Кутузов и Наполеон в романе Л.Н. Толстого «Война и мир» SMM. Работа с лидерами мнений
SMM. Работа с лидерами мнений Меры государственной поддержки для инвесторов на территории республики Башкортостан
Меры государственной поддержки для инвесторов на территории республики Башкортостан РАЗВИТИЕ ТВОРЧЕСКИХ СПОСОБНОСТЕЙ НА УРОКАХ ТЕХНОЛОГИИ
РАЗВИТИЕ ТВОРЧЕСКИХ СПОСОБНОСТЕЙ НА УРОКАХ ТЕХНОЛОГИИ Эмблемы и знаки отличия родов войск РФ
Эмблемы и знаки отличия родов войск РФ О повышении доступности и качества банковских услуг в целях обеспечения динамичного развития экономики Краснодарского края в 2012
О повышении доступности и качества банковских услуг в целях обеспечения динамичного развития экономики Краснодарского края в 2012  Республика
Республика «Храм Покрова на Нерли – жемчужина архитектуры Владимиро-Суздальской Руси (XII в.)»
«Храм Покрова на Нерли – жемчужина архитектуры Владимиро-Суздальской Руси (XII в.)» Captain America
Captain America  Прибыль. Финансы и кредит
Прибыль. Финансы и кредит Антикоррупционная политика образовательной организации
Антикоррупционная политика образовательной организации Государство: понятие и признаки
Государство: понятие и признаки Свод правил. Общественные здания
Свод правил. Общественные здания Создание удаленного сервера
Создание удаленного сервера Mobile web
Mobile web Что нам осень принесла
Что нам осень принесла Диаграммы состояния сплавов
Диаграммы состояния сплавов Запеченное мясо
Запеченное мясо Парк им. Ленина на берегу реки Белой
Парк им. Ленина на берегу реки Белой Марафон стройности
Марафон стройности Укупорочные средства
Укупорочные средства 20140928_vulkany_i_geyzery_1_
20140928_vulkany_i_geyzery_1_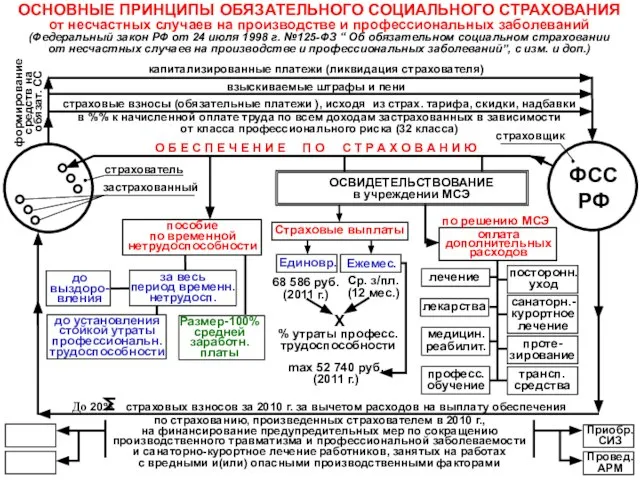 ФСС РФ
ФСС РФ