Способы задания плоскости

Набор параметров,
выделяющих единственную плоскость, называется ее
определителем (∆)
Плоскость, произвольно расположенная в пространстве, называется плоскостью общего положения

х
А2
В2
С2
С1
А1
В1
х
А2
В2
С2
С1
А1
В1
х
А2
D2
С2
С1
А1
В1
В2
D2
//
//
//
//
1. Тремя точками, не лежащими на одной прямой
2. Прямой и точкой вне прямой
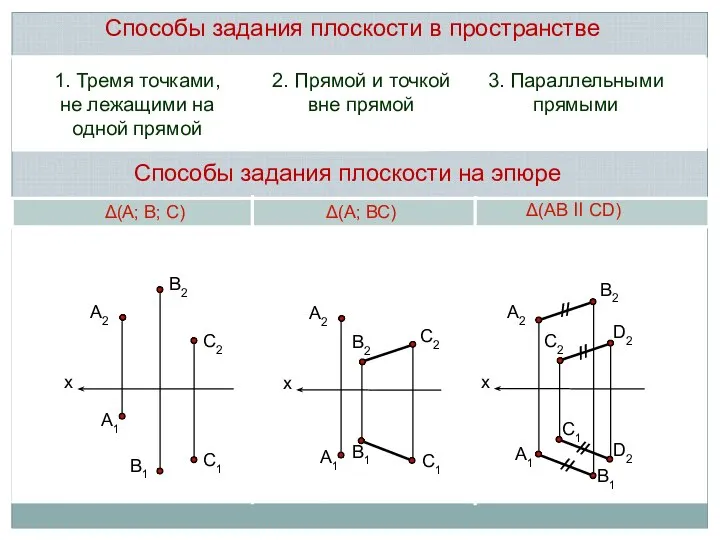
3. Параллельными прямыми
Δ(А; В; С)
Δ(А; ВС)
Δ(АВ ll СD)
Способы задания плоскости в пространстве
Способы задания плоскости на эпюре

х
А2
В2
С2
С1
А1
В1
Δ(АВ∩BС)
х
А2
В2
С2
С1
А1
В1
Δ( АВС)
4. Пересекающимися прямыми
5. Плоской фигурой (отсеком плоскости)
6. Следами
х
Px
Pz
Py
Py
pП1
pП2
z
y
Δ(АВ∩ВС)
Δ(ΔАВС)
Δ(рП1; рП2; рП3)
pП3
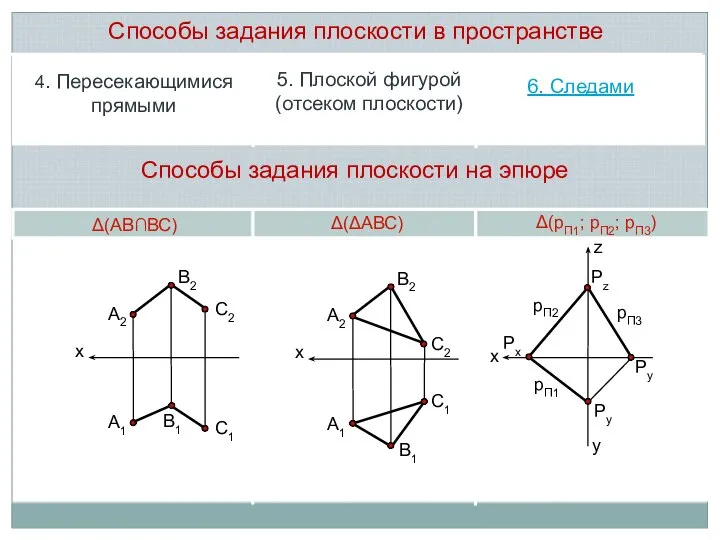
Способы задания плоскости в пространстве
Способы задания плоскости на эпюре