Содержание
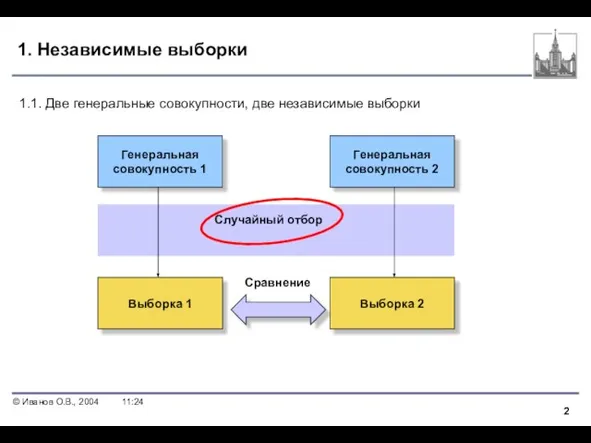
- 2. 1. Независимые выборки Генеральная совокупность 1 Генеральная совокупность 2 Выборка 1 Выборка 2 1.1. Две генеральные
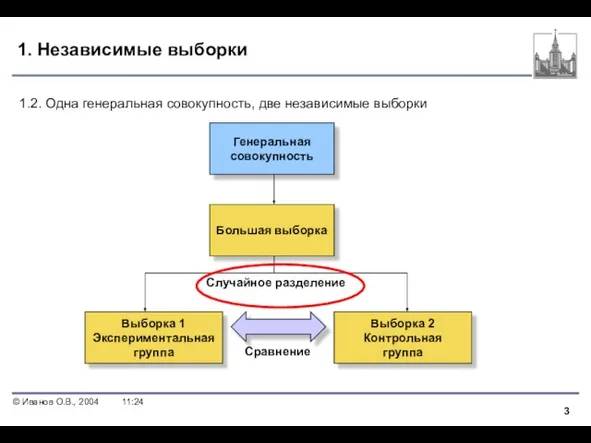
- 3. 1. Независимые выборки Генеральная совокупность Выборка 1 Экспериментальная группа Выборка 2 Контрольная группа 1.2. Одна генеральная
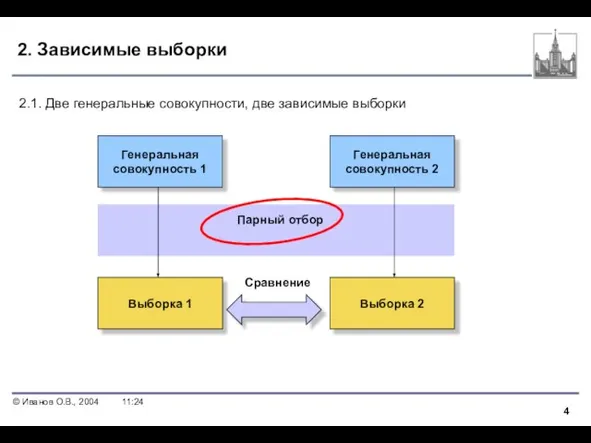
- 4. 2. Зависимые выборки Генеральная совокупность 1 Генеральная совокупность 2 Выборка 1 Выборка 2 2.1. Две генеральные
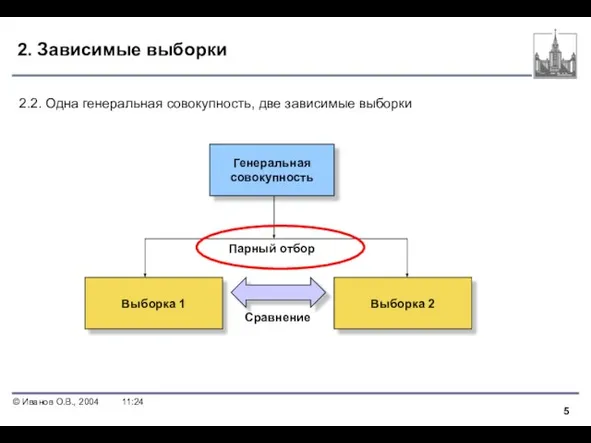
- 5. 2. Зависимые выборки Генеральная совокупность Выборка 1 Выборка 2 2.2. Одна генеральная совокупность, две зависимые выборки
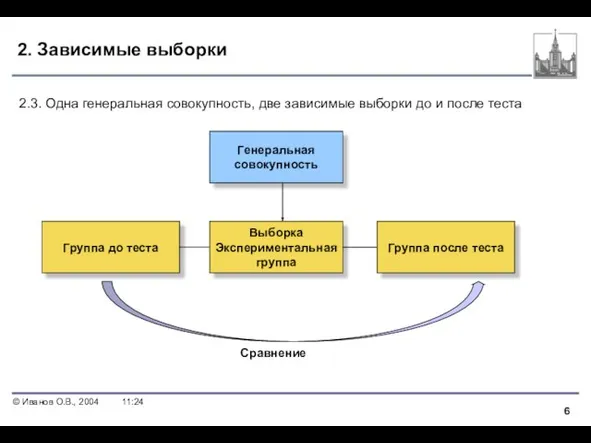
- 6. 2. Зависимые выборки Генеральная совокупность Группа до теста Группа после теста 2.3. Одна генеральная совокупность, две
- 7. 10.1. Гипотеза о равенстве средних. Независимые выборки
- 8. Независимые выборки. Описание проблемы Что мы имеем 1. Две простые случайные выборки, полученные из двух генеральных
- 9. Гипотеза Нулевая гипотеза: Это равносильно гипотезе: Альтернативная гипотеза:
- 10. Односторонние гипотезы Нулевая гипотеза: Или, что равносильно: Альтернативная гипотеза: Правосторонний критерий Левосторонний критерий
- 11. 1. Статистика (σ1 и σ2 известны) Для проверки гипотезы используется статистика: где - выборочные средние -
- 12. Почему выбирает этот критерий? В качестве критерия мы выбираем: Наблюдаемое значение: Ожидаемое значение: Стандартная ошибка: Это
- 13. Последовательность действий Шаг 1. Сформулировать основную и альтернативную гипотезы. Шаг 2. Задать уровень значимости α. Шаг
- 14. Задача. Стоимость ремонта Частная исследовательская фирма тестировала две различных марки автомобиля, с целью определить, есть ли
- 15. Решение Шаг 1. Основная и альтернативная гипотезы: Шаг 2. Задан уровень значимости α=0,05. Шаг 3. По
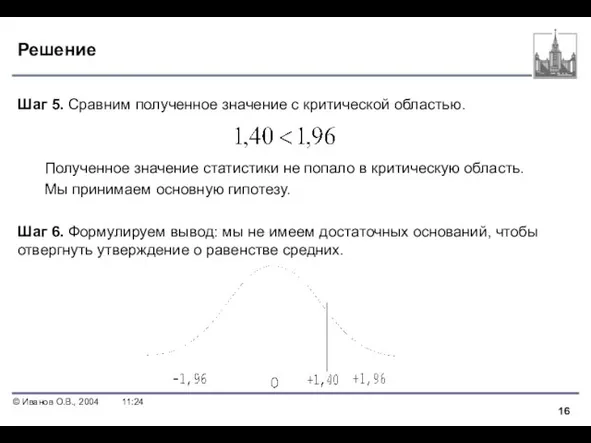
- 16. Решение Шаг 5. Сравним полученное значение с критической областью. Полученное значение статистики не попало в критическую
- 17. Если дисперсии не известны… Как проверить гипотезу о равенстве средних, если дисперсии генеральной совокупности не известны?
- 18. 2. Статистика (σ1 и σ2 не известны и не равны) Для проверки гипотезы используется статистика: где
- 19. 3. Статистика (предполагаем σ1 = σ2) Для проверки гипотезы используется статистика: где - выборочные средние -
- 20. Объединенная дисперсия (Pooled variance) Если нам известно, что дисперсии генеральных совокупностей равны, или мы проверяем гипотезу,
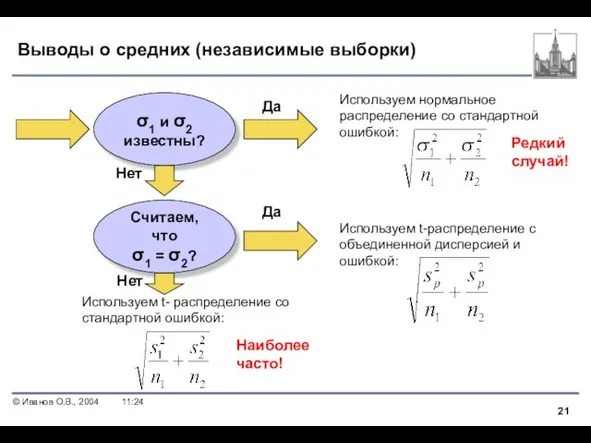
- 21. Выводы о средних (независимые выборки) σ1 и σ2 известны? Считаем, что σ1 = σ2? Используем нормальное
- 22. 10.2. Доверительный интервал для разности средних
- 23. Описание проблемы Что мы имеем Имеем две простые случайные, независимые выборки объема n1 и n2 из
- 24. Доверительный интервал для разности средних (1) Среднее генеральной совокупности с надежностью 1-α/2 находится в доверительном интервале:
- 25. Доверительный интервал для разности средних (2) Среднее генеральной совокупности с надежностью 1-α/2 находится в доверительном интервале:
- 26. Доверительный интервал для разности средних (3) Среднее генеральной совокупности с надежностью 1-α/2 находится в доверительном интервале:
- 27. Пример Преподаватель хочет оценить различия в оценках студентов-вечерников и студентов-дневников. Ниже приведены результаты экзамена. Построить 95%
- 28. 10.3. Гипотеза о равенстве средних. Парные выборки
- 29. Парные выборки. Описание проблемы Что мы имеем 1. Две простые случайные выборки, полученные из двух генеральных
- 30. Статистика для парных выборок Для проверки гипотезы используется статистика: где - разность между двумя значениями x
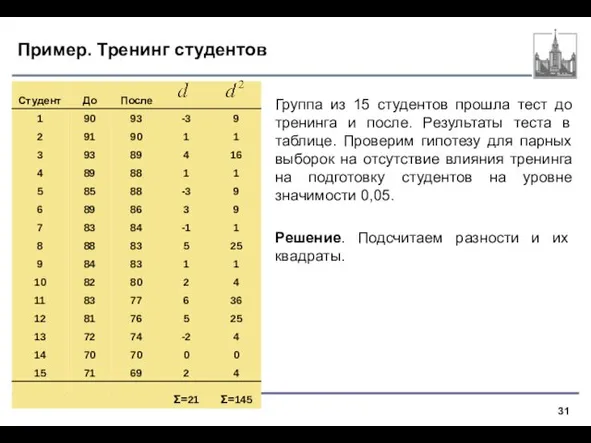
- 31. Пример. Тренинг студентов Группа из 15 студентов прошла тест до тренинга и после. Результаты теста в
- 32. Решение Шаг 1. Основная и альтернативная гипотезы: Шаг 2. Задан уровень значимости α=0,05. Шаг 3. По
- 33. Решение Статистика принимает значение: Среднее значение разностей получено делением 21 на 15 и равно 1,4.
- 34. Решение Шаг 5. Сравним полученное значение с критической областью. Полученное значение статистики не попало в критическую
- 35. 10.4. Доверительный интервал для разности средних. Парные выборки
- 36. Зависимые выборки. Описание проблемы Что мы имеем Имеем две случайные парные (зависимые) выборки объема n из
- 37. Доверительный интервал Среднее разности парных значений между двумя генеральными совокупностями с надежностью 1-α/2 находится в доверительном
- 38. Пример построения доверительного интервала Выборка включает 15 студентов, следовательно df = 15 – 1 = 14.
- 39. 10.5. Гипотеза о равенстве дисперсий
- 40. В ходе исследования… Исследователю может понадобиться проверить предположение, о равенстве дисперсий двух изучаемых генеральных совокупностей. В
- 41. Описание проблемы Что мы имеем 1. Две простые случайные выборки, полученные из двух нормально распределенных генеральных
- 42. Обозначения Дисперсии генеральных совокупностей: Дисперсии двух выборок: Объемы двух выборок: Подбираем, чтобы обязательно:
- 43. Гипотеза Нулевая гипотеза: Альтернативная гипотеза: Других альтернативных гипотез в этом критерии не рассматривается.
- 44. Статистика Для проверки гипотезы используется статистика: Если гипотеза верна, эта статистика имеет F-распределение (распределение Фишера) с
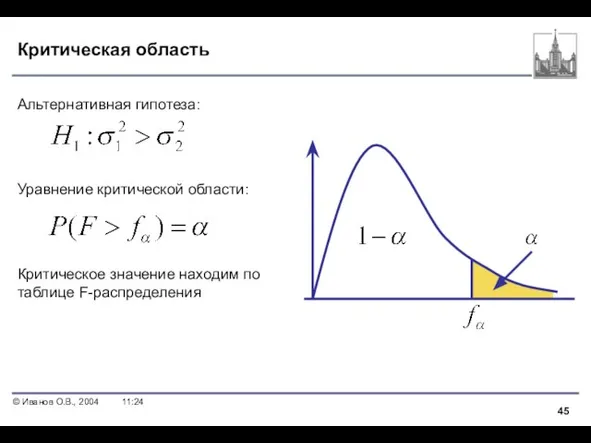
- 45. Критическая область Альтернативная гипотеза: Уравнение критической области: Критическое значение находим по таблице F-распределения
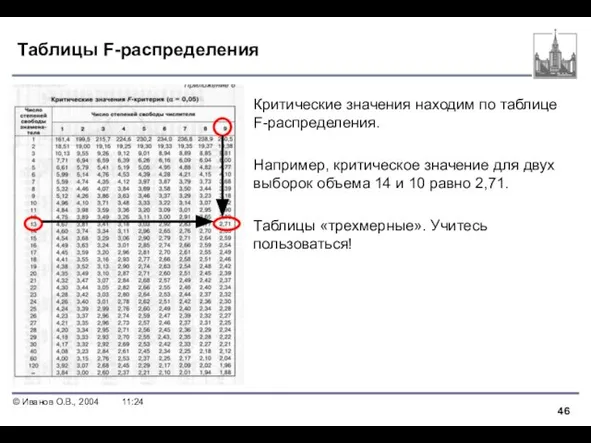
- 46. Таблицы F-распределения Критические значения находим по таблице F-распределения. Например, критическое значение для двух выборок объема 14
- 47. Пример. Исследователь-медик хочет проверить, есть ли различие между частотой биения сердца курящих и некурящих пациентов (кол-во
- 48. Решение Шаг 1. Основная и альтернативная гипотезы: Шаг 2. Задан уровень значимости α=0,05. Шаг 3. По
- 49. Решение Шаг 5. Сравним полученное значение с критической областью. Полученное значение статистики попало в критическую область.
- 50. 10.6. Гипотеза о равенстве долей
- 51. Вопрос Из 100 случайно отобранных студентов социологического факультета 43 посещают спецкурсы. Из 200 случайно отобранных студентов-экономистов
- 52. Описание проблемы Что мы имеем 1. Две простые случайные выборки, полученные из двух нормально распределенных генеральных
- 53. Обозначения - объемы выборок - количество «успехов» в каждой выборке - доля «успехов» в первой выборке
- 54. Статистика В качестве статистики выбираем следующую случайную функцию: Для проверки гипотезы пользуемся таблицей нормального распределения.
- 55. Пример. Из 100 случайно отобранных студентов социологического факультета 43 посещают спецкурсы. Из 200 студентов-экономистов 90 человек
- 56. Решение Вычислим необходимые значения:
- 57. Решение Шаг 1. Основная и альтернативная гипотезы: Шаг 2. Задан уровень значимости α=0,05. Шаг 3. По
- 58. Решение Шаг 5. Сравним полученное значение с критической областью. Полученное значение статистики не попало в критическую
- 59. 10.7. Доверительный интервал для разности долей
- 60. Доверительный интервал для разности долей Доля значений признака в генеральной совокупности с надежностью 1-α/2 находится в
- 61. Пример Предположим, по результатам исследования 40% из 200 мужчин и 56% из 100 женщин высказались против
- 62. Понятия и термины
- 63. Задание на 5 минут От чего и каким образом зависит критическая область?
- 64. Задачи 10.1. Преподаватель хочет понять, действительно ли студенты-вечерники получают более высокие баллы по сравнению с учащимися
- 65. Задачи 10.2. Исследователь хочет сравнить скорость реакции таксистов и полицейских. Полученные им результаты представлены ниже. Может
- 66. Задачи 10.3. Исследователь предполагает, что среди учеников средней школы девочки чаще, чем мальчики, прогуливают занятия. Выборочное
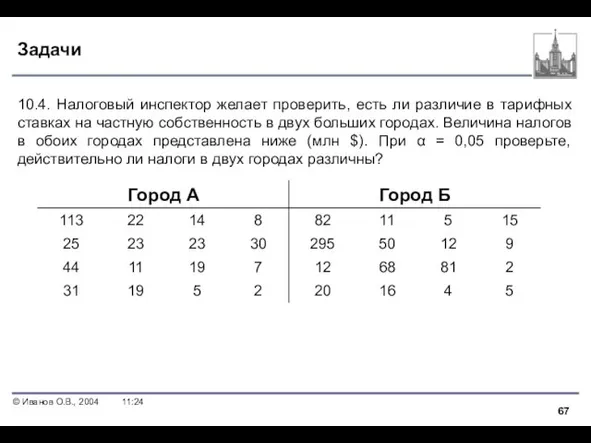
- 67. Задачи 10.4. Налоговый инспектор желает проверить, есть ли различие в тарифных ставках на частную собственность в
- 68. Задачи 10.5. Преподаватель считает, что студенты, специализация которых – математика, могут написать компьютерную программу быстрее, чем
- 69. Задачи 10.6. Местное отделение налоговой инспекции потратило примерно по 21 минуте на то, чтобы помочь каждому
- 70. Задачи 10.7. Преподаватель утверждает, что когда преподавание курса идет с использованием лекций, то дисперсия успеваемости больше,
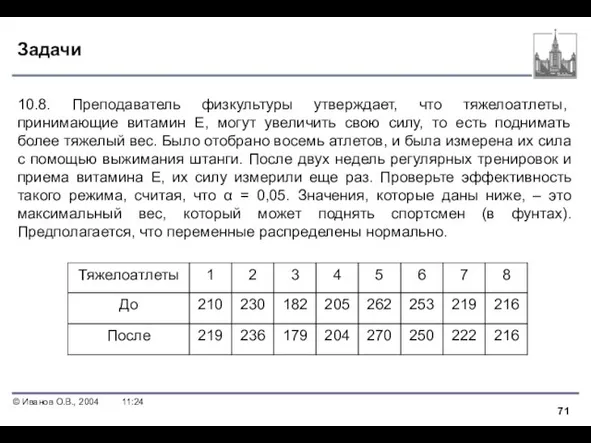
- 71. Задачи 10.8. Преподаватель физкультуры утверждает, что тяжелоатлеты, принимающие витамин Е, могут увеличить свою силу, то есть
- 72. Задачи 10.9. Социологу интересно узнать, повлияет ли показ фильма об управлении стрессом, на установки двенадцати человек,
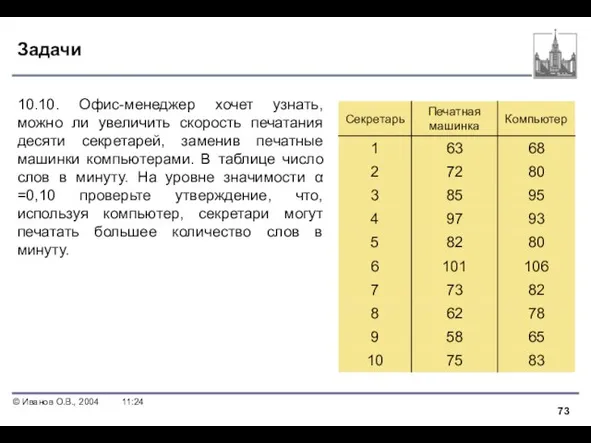
- 73. Задачи 10.10. Офис-менеджер хочет узнать, можно ли увеличить скорость печатания десяти секретарей, заменив печатные машинки компьютерами.
- 74. Задачи 10-11. В результате исследования выяснилось, из 100 опрошенных мужчин 83% предпочитают лекциям обучение с помощью
- 75. Задачи 10-15. В первой выборке из 100 человек 30% были в Диснейленде, а во второй (тоже
- 77. Скачать презентацию




























































 Компьютер и здоровье глаз
Компьютер и здоровье глаз Пейзаж.Времена года
Пейзаж.Времена года Организационное и информационное обеспечение фандрейзинга
Организационное и информационное обеспечение фандрейзинга Сложноподчиненное предложение. Повторение и обобщение изученного.
Сложноподчиненное предложение. Повторение и обобщение изученного. История радио и мобильной связи
История радио и мобильной связи А как ты знаешь физику?
А как ты знаешь физику? Презентация на тему Нефтяная промышленность
Презентация на тему Нефтяная промышленность  Изобразительное искусство барокко
Изобразительное искусство барокко Как начать бизнес в интернете?
Как начать бизнес в интернете? Sony Ericsson: Из VGA в HD
Sony Ericsson: Из VGA в HD Символика Краснодарского края
Символика Краснодарского края Для умных женщин Одна супружеская пара поехала в выходные на озеро порыбачить.
Для умных женщин Одна супружеская пара поехала в выходные на озеро порыбачить. Бюджет для граждан по Решению Совета депутатов МО Александровский район от 23.12.2020
Бюджет для граждан по Решению Совета депутатов МО Александровский район от 23.12.2020 Children's behavior and its influence on their future acts
Children's behavior and its influence on their future acts РАНХиГС_очно_27.09.2022_Акцнт, реф, защ, техн ОС
РАНХиГС_очно_27.09.2022_Акцнт, реф, защ, техн ОС Слова-паразиты, или экология речи
Слова-паразиты, или экология речи Иммунная система и канцерогенез
Иммунная система и канцерогенез  Подарки AI Journey. Предложения. Сберклауд
Подарки AI Journey. Предложения. Сберклауд Философские теории неврозов
Философские теории неврозов Реализация и изучение игры «Жизнь» в среде электронных таблиц (MS Ecxel)
Реализация и изучение игры «Жизнь» в среде электронных таблиц (MS Ecxel) Деструктивность учащегося и образовательной среды: точки соприкосновения
Деструктивность учащегося и образовательной среды: точки соприкосновения БАЛАНС-2W: ПОДГОТОВКА СПРАВКИ 2-НДФЛ
БАЛАНС-2W: ПОДГОТОВКА СПРАВКИ 2-НДФЛ Подготовка граждан к военной службе
Подготовка граждан к военной службе Ультразвуковые накладные расходомеры Flexim
Ультразвуковые накладные расходомеры Flexim Презентация для заказных проектов
Презентация для заказных проектов Поступление на государственную службу
Поступление на государственную службу Оценка достижений учащихся в разновозрастной группе
Оценка достижений учащихся в разновозрастной группе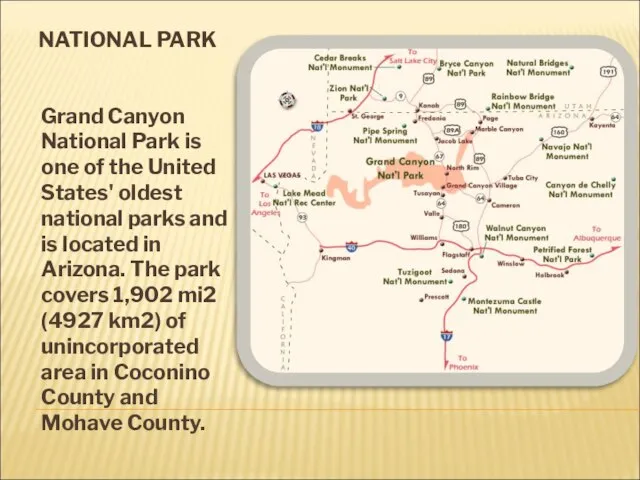 Grand Canyon National Park
Grand Canyon National Park