Содержание
- 2. Objectives Understands the concepts of stacks Representation of stacks as data structure Different method for implementing
- 3. What is a stack? It is an ordered group of homogeneous items of elements. Elements are
- 4. Use of stack in Computer Science Consider an example, where we are executing function A. main()
- 5. Use of stack in Computer Science In the course of its execution, function A calls another
- 6. The system stack ensures a proper execution order of functions. Therefore, stacks are frequently used in
- 7. Operation on Stack push(i) to insert the element i on the top of the stack pop(
- 8. ARRAY REPRESENTATION OF STACKS In the computer’s memory, stacks can be represented as a linear array.
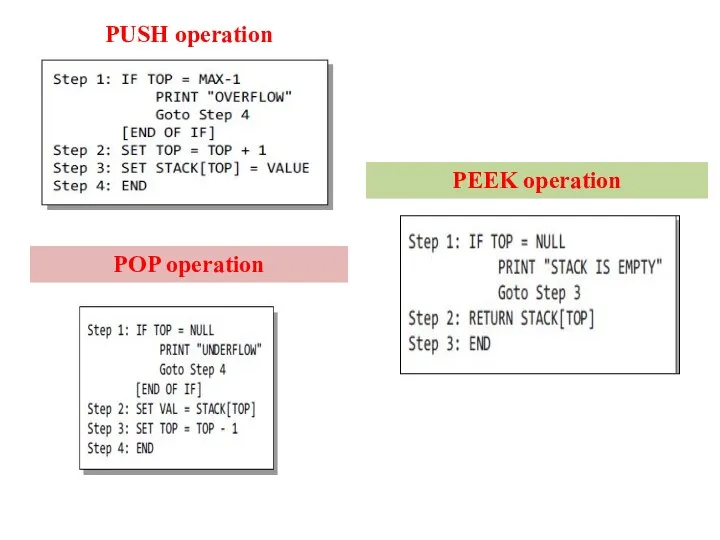
- 9. Algorithm for PUSH operation
- 12. PUSH operation
- 13. LINKED REPRESENTATION OF STACK Stack may be created using an array. This technique of creating a
- 14. Algorithm for PUSH operation of Stack implemented using Linked list
- 15. Algorithm for POP operation of Stack implemented using Linked list
- 16. Algorithm for PUSH operation Algorithm for POP operation
- 17. APPLICATIONS OF STACKS Parentheses checker Conversion of an infix expression into a postfix expression Evaluation of
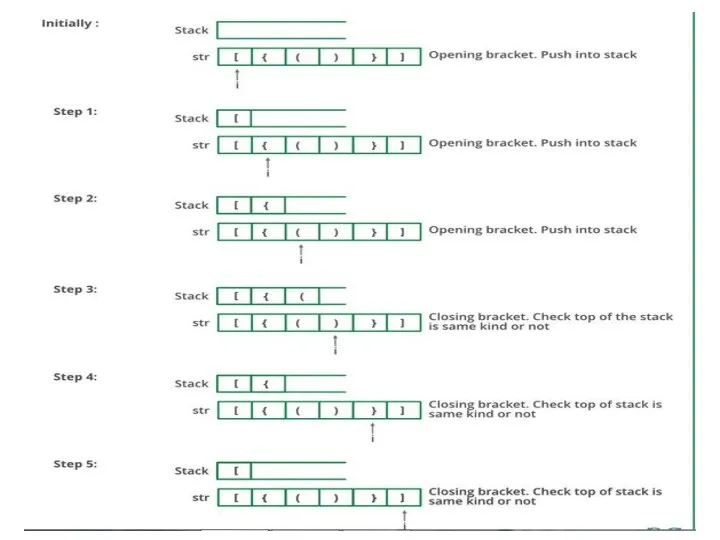
- 18. Parentheses Checker Stacks can be used to check the validity of parentheses in any algebraic expression.
- 19. Algorithm: Declare a character stack S. Now traverse the expression string exp. If the current character
- 21. Pseudo code: Parenthesis Matching valid = true /* assuming that the string is valid*/ s =
- 22. Mathematical Notation Translation prefix (polish) postfix (reverse polish)
- 23. Mathematical Notation Translation Infix – prefix (polish) Infix – postfix (reverse polish) The fundamental property of
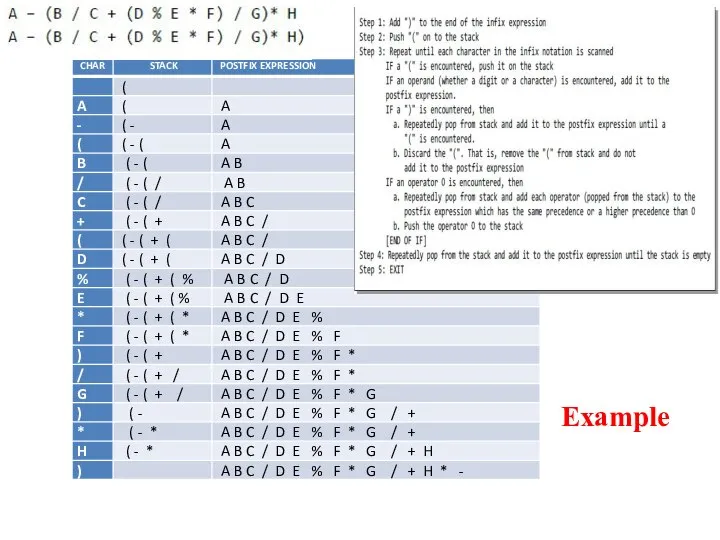
- 24. Conversion of an Infix Expression into a Postfix Expression An algebraic expression may contain parentheses, operands,
- 25. Algorithm Infix Expression to a Postfix Expression
- 26. Example
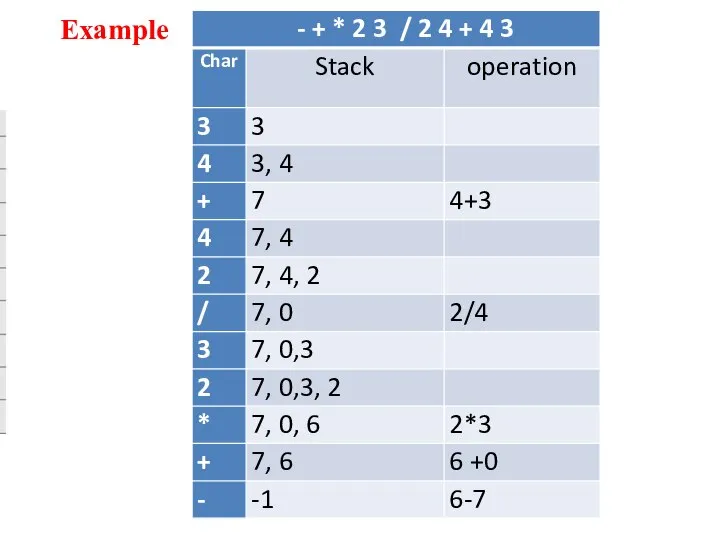
- 27. Evaluation of a Postfix Expression
- 28. Evaluation of a Postfix Expression
- 29. Example
- 30. Infix to Prefix Expression
- 31. Step 1. Push “)” onto STACK, and add “(“ to start of the A. Step 2.
- 32. Method2- Infix Expression to a Prefix Expression
- 33. Step 1. Push “)” onto STACK, and add “(“ to start of the A. Step 2.
- 35. Evaluation of a Prefix Expression
- 36. Example
- 38. Скачать презентацию































 Вудлин Парк
Вудлин Парк Презентация на тему Черемуха С. Есенин
Презентация на тему Черемуха С. Есенин  Как правильно ставить цели и достигать их
Как правильно ставить цели и достигать их Презентация на тему Архиватор
Презентация на тему Архиватор Мир глазами историка
Мир глазами историка Презентация на тему Индия под властью англичан
Презентация на тему Индия под властью англичан Мост Дружбы между славянскими школами
Мост Дружбы между славянскими школами Лущение древесины
Лущение древесины РГУ нефти и газа им. И.М. Губкина
РГУ нефти и газа им. И.М. Губкина Увлекательная и полезная арт-терапия
Увлекательная и полезная арт-терапия КАТАЛИЗАТОРЫ И БАРЬЕРЫ РАЗВИТИЯ ИННОВАЦИОННОЙ ДЕЯТЕЛЬНОСТИ (НОРМАТИВНЫЙ ПРАВОВОЙ АСПЕКТ)Васильев В. Н.
КАТАЛИЗАТОРЫ И БАРЬЕРЫ РАЗВИТИЯ ИННОВАЦИОННОЙ ДЕЯТЕЛЬНОСТИ (НОРМАТИВНЫЙ ПРАВОВОЙ АСПЕКТ)Васильев В. Н. Учебный центр “Эврика”
Учебный центр “Эврика” Модерн в Казани
Модерн в Казани Адитим_Практикум 7_Продающая презентация
Адитим_Практикум 7_Продающая презентация Документооборот. Ведение базы данных документов организации
Документооборот. Ведение базы данных документов организации Паралимпийцы Оренбургской области
Паралимпийцы Оренбургской области Презентация на тему "Повышение уровня социальной адаптации учащихся с ОВЗ, на уроках математики, экономики и компьютерной грамо
Презентация на тему "Повышение уровня социальной адаптации учащихся с ОВЗ, на уроках математики, экономики и компьютерной грамо Ежегодный творческий конкурс«Урок Просвещения - 2011»
Ежегодный творческий конкурс«Урок Просвещения - 2011» Материальная часть стрелкового оружия и ручных осколочных гранат
Материальная часть стрелкового оружия и ручных осколочных гранат Презентация на тему Военная форма одежды и знаки различия
Презентация на тему Военная форма одежды и знаки различия «И снизу лед…»
«И снизу лед…» «HR-ассоциация: решение задач бизнеса, условия для развития личности»
«HR-ассоциация: решение задач бизнеса, условия для развития личности» Тема 2.2
Тема 2.2 ОТЧЕТ ЗА ДЕЙНОСТТА НА МИНИСТЕРСТВО НА ЗЕМЕДЕЛИЕТО И ХРАНИТЕ ЗА ПЕРИОДА 27 ЮЛИ 2009 Г.- 27 ЮЛИ 2010 Г.
ОТЧЕТ ЗА ДЕЙНОСТТА НА МИНИСТЕРСТВО НА ЗЕМЕДЕЛИЕТО И ХРАНИТЕ ЗА ПЕРИОДА 27 ЮЛИ 2009 Г.- 27 ЮЛИ 2010 Г. Баскетбол
Баскетбол Мастерство работника
Мастерство работника Человек: анатомия, физиология и медицина
Человек: анатомия, физиология и медицина Презентация на тему Пищевая промышленность: рынок мяса
Презентация на тему Пищевая промышленность: рынок мяса