Статичне електричне поле

Заряди
Ми знаємо про явище електризації, про існування електричного заряду, про наявність двох видів зарядів (умовно додатних та від'ємних) та взаємодії між ними.
Заряди – невід'ємна частина переважної більшості елементарних частинок. Вони строго однакові за величиною і дорівнюють елементарному заряду. Якщо кількість позитивних і негативних зарядів однакова, тіло незаряджене. Коли інакше, різниця кількості цих зарядів визначає заряд тіла. Можна розвести заряди в різні боки. Тоді окремі частини тіла будуть заряджені. Загальний заряд тіла кратний елементарному заряду: q = Ne. Електричні заряди виникають і зникають попарно, а сумарний заряд залишається незмінним (закон збереження заряду).

Заряди
Якщо заряди вільно переміщуються по тілу, то це тіло є провідником. Проте, носіями струму можуть бути як електрони так і іони, тобто атоми чи молекули, які втратили чи приєднали один чи кілька електронів.
У відповідності зі здатністю тіла проводити струм всі речовини поділяються на діелектрики (ізолятори), напівпровідники і провідники.
Ідеальних діелектриків немає, реальні діелектрики проводять струм в 1015÷1020 раз гірше, ніж провідники.
Напівпровідники займають проміжний стан.

Взаємодія між зарядами
Закон взаємодії встановлений в 1785 р. Кулоном. Він
знайшов
Якщо f > 0, маємо відштовхування, а
при f < 0 – притягання.
Знаючи закон для точкових зарядів,
можна знайти силу взаємодії між
тілами. Для цього розбиваємо тіло
на елементи заряду dq і інтегруємо
по об'єму.

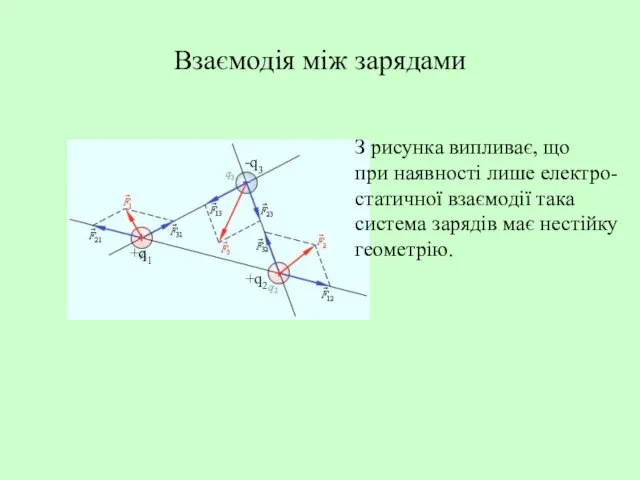
Взаємодія між зарядами
+q1
+q2
-q3
З рисунка випливає, що
при наявності лише електро-
статичної взаємодії така
система зарядів має нестійку
геометрію.

Заряд
Оскільки за часів Кулона не було одиниці електричного заряду, можна було вибрати її так, щоб k = 1. Це така величина зарядів (q1 = q2), яка на відстані 1 см діє з силою 1 дина = 10-5 Н (система СГСЕ). В цій системі елементарний заряд має величину 4,8·10-10 од. зар. СГСЕ.
При переході до системи СІ, де електричні і магнітні величини знаходять із закону взаємодії провідників зі струмом, одиницею заряду є 1 Кулон, величина
При цьому 1 Кл = 3·109 од. СГСЕ, елементарний заряд
е = 1,60217733·10-19 Кл.

Електричне поле
Взаємодія між зарядами здійснюється через електричне поле. Поле виявляється тим, що на вміщений в нього заряд діє сила. Заряд, з допомогою якого досліджують поле, називається пробним. Тоді
q qпр
• •
f
Коли qпр різні, то різна і сила f. Проте, величина f/qпр
залишається постійною і визначає електричне поле в
точці.
Тому - напруженість електричного поля.

Електричне поле
Напрям вектора збігається з напрямом сили, що діє на заряд q, поміщений в поле:
Поле від багатьох зарядів складається за правилом векторного складання
Скористаємось цим правилом для знаходженні поля диполя – системи двох однакових за величиною і протилежних за напрямом полів.

Електричне поле диполя
Знайдемо залежність напруженості електричного поля диполя в залежності від відстані r на лінії, рівновіддаленій від зарядів. В цьому випадку
+q
-q
ℓ
r
E+
E-
E
Враховуючи, що дипольний момент p = qℓ
і те, що на великих відстанях
знаходимо

Силові лінії електричного диполя
Для довільного напрямку величина електричного поля
визначається за формулою
θ

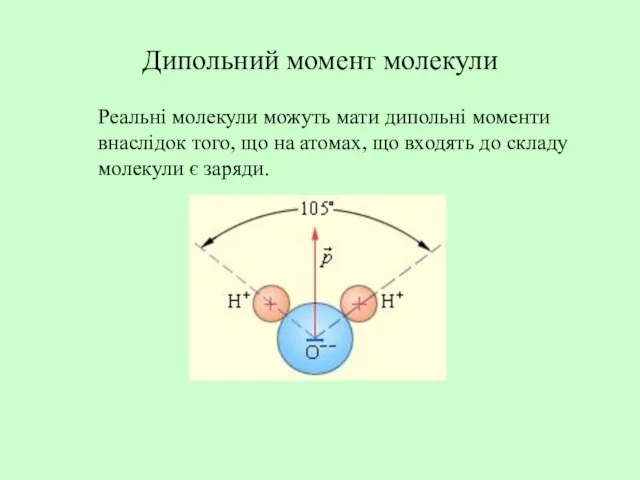
Дипольний момент молекули
Реальні молекули можуть мати дипольні моменти
внаслідок того, що на атомах, що входять до складу
молекули є заряди.

Електричне поле мультиполів
Розглянемо 4 однакових за абсолютною величиною заряди на вершинах квадрата. В цьому випадку на великих відстанях напруженість поля
q
q
-q
-q
q
q
q
q
-q
-q
-q
Конструкція з 8 зарядів на вершинах куба
називається октуполем. В цьому випадку

Силові лінії електростатичного поля
Сукупність векторів в просторі утворює поле вектора
напруженості. Тому можна електричне поле описати за
допомогою ліній . Дотична до ліній визначає напрям
поля, густота ліній – величину .
Повне число ліній, що
перетинає поверхню
радіуса r
не залежить від r.

Потік через замкнуту поверхню
Кількість ліній, що пронизує площадку dS:
Отже, потік чисельно дорів-
нює кількості ліній, що про-
низують поверхню.

Застосування теореми Остроградського-Гауса
Згідно з теоремою Остроградського-Гауса
де ρ – об'ємна густина електричного заряду.
Крім об'ємної густини можна ввести поверхневу та лінійну
густину

Поле рівномірно зарядженої площини
Розглянемо поле рівномірно зарядженої площини,
σ = const. З симетрії випливає, що поле завжди ⊥ до
поверхні. Виріжемо тонкий циліндр ⊥ до площини.
Застосуємо теорему Острогра-
дського-Гауса. Потік через
бокові поверхні відсутній, а
через 2 основи циліндра 2EdS.
Маємо однорідне поле, не
залежить від відстані.

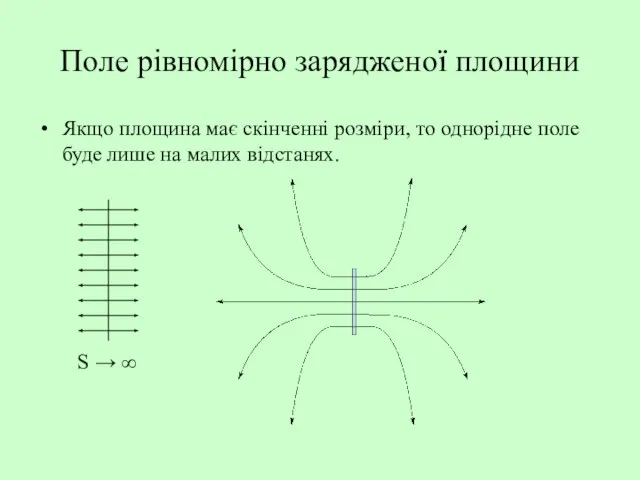
Поле рівномірно зарядженої площини
Якщо площина має скінченні розміри, то однорідне поле буде лише на малих відстанях.
S → ∞

Поле двох рівномірно заряджених площин
Візьмемо дві паралельні різнойменно заряджені площини.
+q
-q
В цьому випадку між пластинами поля
складаються, даючи подвійну напруже-
ність, а за межами пластин поля відні-
маються, внаслідок чого все поле
локалізується між пластинами.

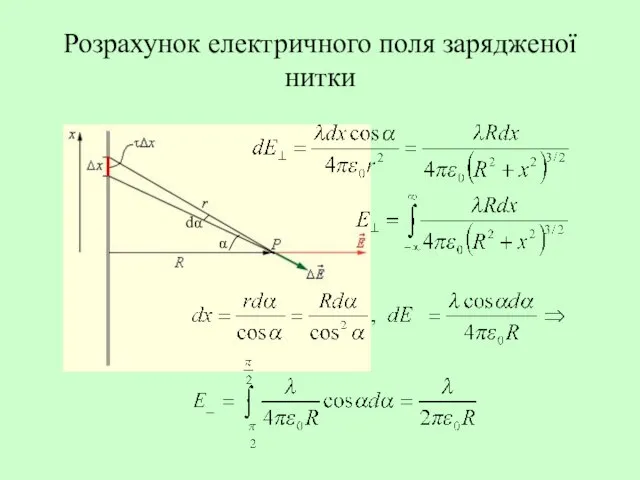
Розрахунок електричного поля зарядженої нитки
α
dα

Поле однорідно зарядженого циліндра
Радіус циліндра R, поверхнева
густина заряду σ. З симетрії ви-
пливає, що поле завжди ⊥ до осі
циліндра.
Замкнемо циліндр коаксіальною
поверхнею – циліндром з радіусом
r і висотою ℓ. Тоді потік
Звідси

Поле однорідно зарядженого циліндра
Якщо виберемо циліндр з r < R, то замкнута поверхня не містить всередині зарядів, внаслідок чого E(r) = 0.
На поверхні циліндра (r = R)

Поле двох коаксіальних циліндрів
Якщо циліндри мають однакові за величиною, але протилежні за знаком заряди, тоді всередині меншого і зовні більшого циліндра поле відсутнє. Поле є лише між циліндрами:

Поле рівномірно зарядженої сферичної поверхні
Сфера радіусу R, поверхнева густина заряду σ. Центральна симетрія. Вектори Е проходять через центр сфери.
Уявимо сферу з радіусом r. Для всіх точок En = E(r). При r > R заряд знаходиться всередині.
При r < R E(r) = 0.
На поверхні r = R

Поле двох концентричних поверхонь
Заряди поверхонь однакові. Все поле між сферами.
Для R1 < r < R2

Поле об'ємно зарядженої сфери
Поле центральної симетрії.
Зовні сфери результат такий же, як і для сфери з зарядженою поверхнею. Але при r < R всередині виділеної сфери заряд
Отже,

Робота сил електричного поля
- не залежить від шляху.
f
1
2
dℓ
Робота виконується за рахунок потенці-
альної енергії: A12 = W1 – W2
При r → ∞ W → 0. Тому W(r) =
Потенціальна енергія W = qφ. Дж = Кл·В

Робота сил електричного поля
В фізиці використовується одиниця енергії і роботи
1 електрон-вольт (еВ).
1 еВ = 1,6·10-19 Кл·1 В = 1,6·10-19 Дж.
Кратні величини: кеВ, МеВ, ГеВ, ТеВ тощо.
Величина kT при кімнатній температурі = 0,025 еВ.
Оскільки
Між двома паралельними поверхнями (в конденсаторі)

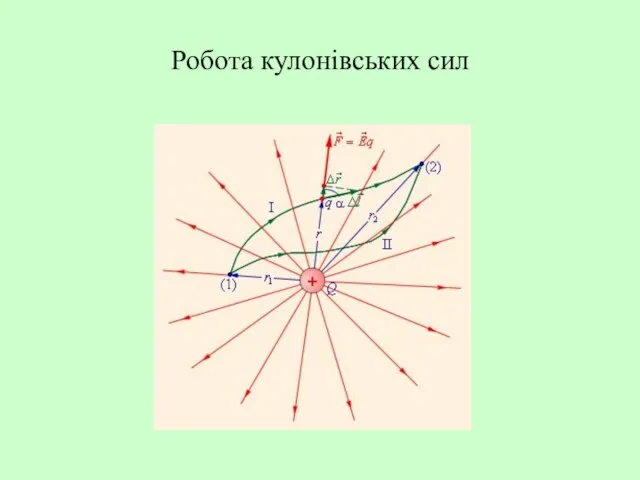
Робота кулонівських сил