Статика

СТАТИКА
Это раздел механики, в котором изучается
условия равновесия абсолютно твердых тел.

В статике учитываются размеры и формы тел и все рассматриваемые тела считаются абсолютно твёрдыми.
Абсолютно твёрдое тело – это тело, взаимное расположение частей которого не изменяется.

Условия равновесия
твёрдого тела:
1.Для равновесия тела необходимо, чтобы сумма внешних сил ,приложенных к телу ,была равна нулю:
F1+F2+…+Fn = 0
2.При равновесии твёрдого тела сумма моментов всех внешних сил, действующих на тело относительно любой оси, равна нулю.
3.Должны быть также равны нулю начальная скорость центра масс и угловая скорость вращения тела.

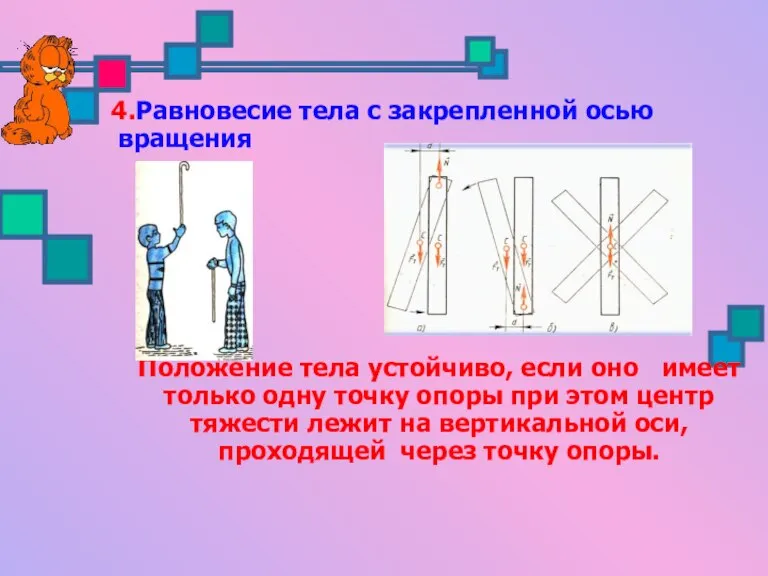
4.Равновесие тела с закрепленной осью вращения
Положение тела устойчиво, если оно имеет только одну точку опоры при этом центр тяжести лежит на вертикальной оси, проходящей через точку опоры.

Равновесие тела
на наклонной плоскости
а) Тело сохраняет положение устойчивого равновесия, если линия действия силы тяжести проходит через основание призмы.
б) В положении, когда линия действия силы тяжести
проходит через границу площади опоры, призма неустойчива.
в) При увеличении угла наклона, линия действия силы тяжести выходит за пределы площади опоры, что приводит к опрокидыванию призмы.

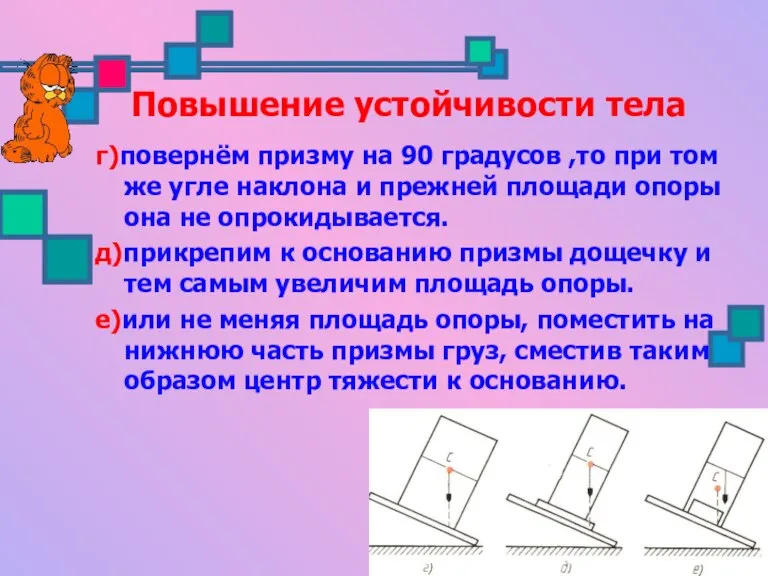
Повышение устойчивости тела
г)повернём призму на 90 градусов ,то при том же угле наклона и прежней площади опоры она не опрокидывается.
д)прикрепим к основанию призмы дощечку и тем самым увеличим площадь опоры.
е)или не меняя площадь опоры, поместить на нижнюю часть призмы груз, сместив таким образом центр тяжести к основанию.

Центр тяжести – точка, через которую проходит равнодействующая всех параллельных сил тяжести, действующая на отдельные элементы тела (при любом положении тела в пространстве).
Момент силы зависит от ее плеча, а значит, и от точки приложения силы.
Особенность силы тяжести - она действует на тело не в одной какой-то точке, а по всему объёму тела. Силы тяжести, действующие на отдельные элементы тела, направлены к центру Земли.
Центр тяжести

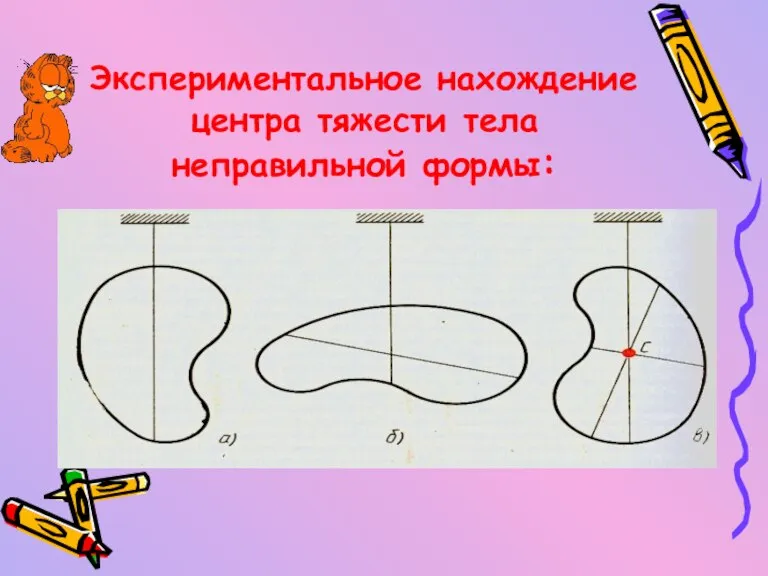
Экспериментальное нахождение центра тяжести тела неправильной формы:

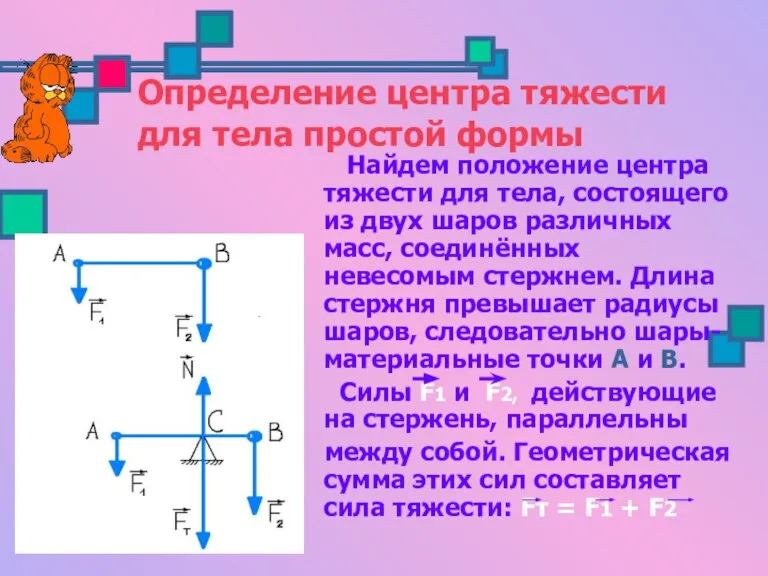
Определение центра тяжести для тела простой формы
Найдем положение центра тяжести для тела, состоящего из двух шаров различных масс, соединённых невесомым стержнем. Длина стержня превышает радиусы шаров, следовательно шары-материальные точки A и B.
Силы F1 и F2, действующие на стержень, параллельны
между собой. Геометрическая сумма этих сил составляет сила тяжести: Fт = F1 + F2

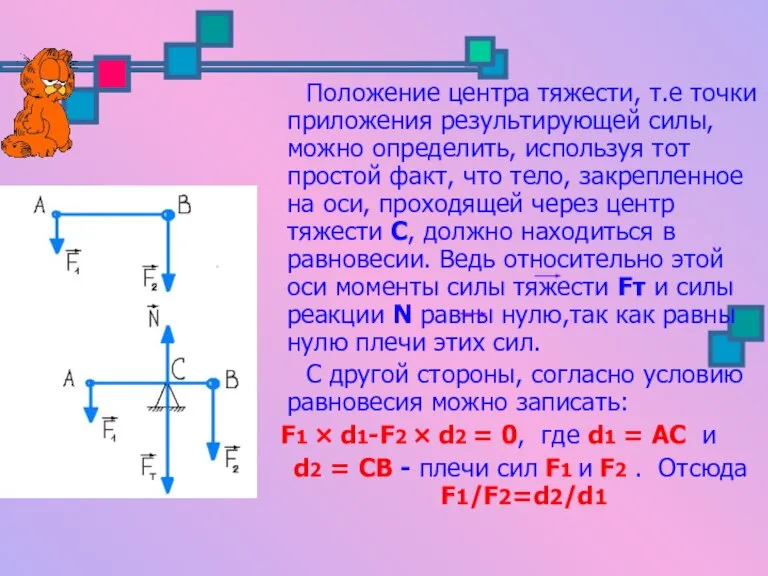
Положение центра тяжести, т.е точки приложения результирующей силы, можно определить, используя тот простой факт, что тело, закрепленное на оси, проходящей через центр тяжести С, должно находиться в равновесии. Ведь относительно этой оси моменты силы тяжести Fт и силы реакции N равны нулю,так как равны нулю плечи этих сил.
С другой стороны, согласно условию равновесия можно записать:
F1 × d1-F2 × d2 = 0, где d1 = AC и
d2 = CB - плечи сил F1 и F2 . Отсюда F1/F2=d2/d1

Таким образом, в случае, когда размеры тела малы по сравнению с расстоянием до центра Земли,
центр тяжести совпадает с центром масс тела.
Сила инерции в неинерциальной системе, движущейся поступательно , приложена всегда к центру масс.

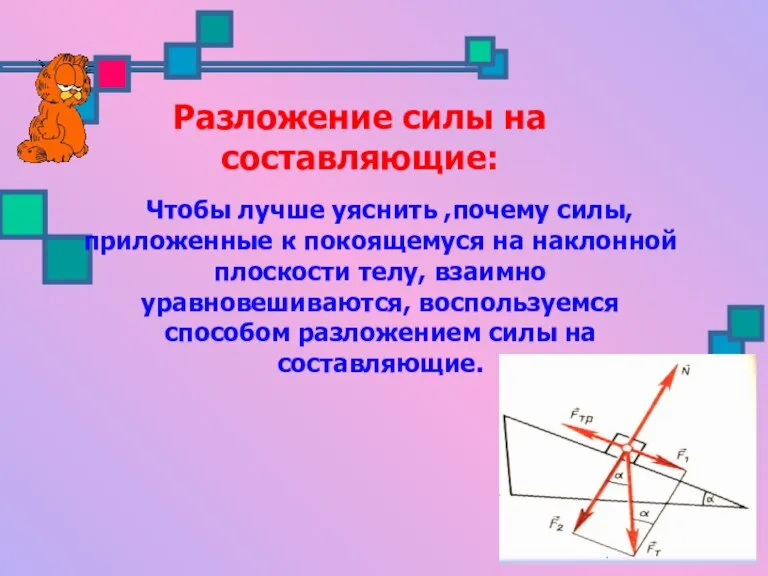
Разложение силы на составляющие:
Чтобы лучше уяснить ,почему силы, приложенные к покоящемуся на наклонной плоскости телу, взаимно уравновешиваются, воспользуемся способом разложением силы на составляющие.

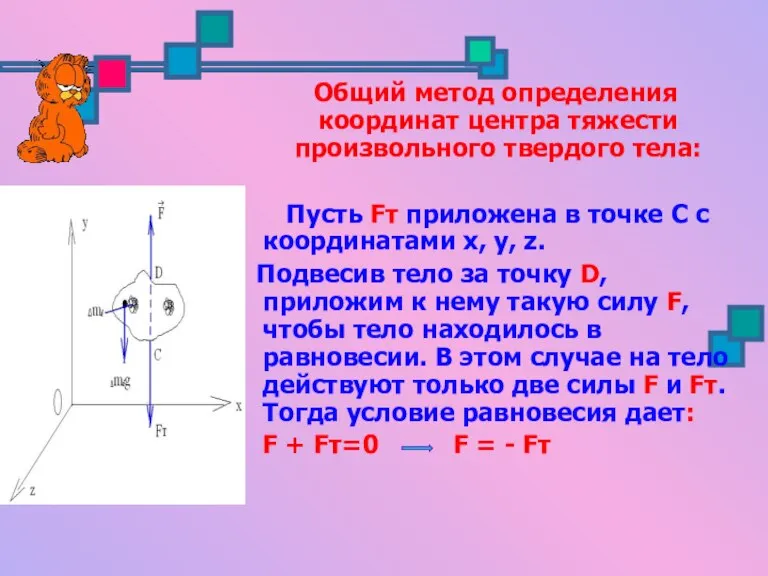
Общий метод определения координат центра тяжести произвольного твердого тела:
Пусть Fт приложена в точке С с координатами х, у, z.
Подвесив тело за точку D, приложим к нему такую силу F, чтобы тело находилось в равновесии. В этом случае на тело действуют только две силы F и Fт. Тогда условие равновесия дает:
F + Fт=0 F = - Fт

Координаты точки приложения равнодействующей всех параллельных сил тяжести:
m
x
F
X

Задача № 1
Шар массой m подвешен на нити и удерживается в отклоненном положении горизонтальной силой F. Найдите угол а, который образует нить с вертикалью при равновесии.
Чему при этом равна сила натяжения нити?
Решение:
На шар действуют три силы: сила тяжести F т=m×g, cила F и сила натяжения нити Т, направленная вдоль нити. По первому условию равновесия T+m×g+F =0 Так как сумма сил равна нулю, то и сумма проекций сил на обе оси координат равна нулю:
T×+m×g+F×=0 T y+m×g+F y=0
или для модулей проекций:
F –T×sin a=0, T×cos a - m×g =0 Отсюда:
tg a=F/(m×g) и T=√ F2+ (m×g) × (m×g)

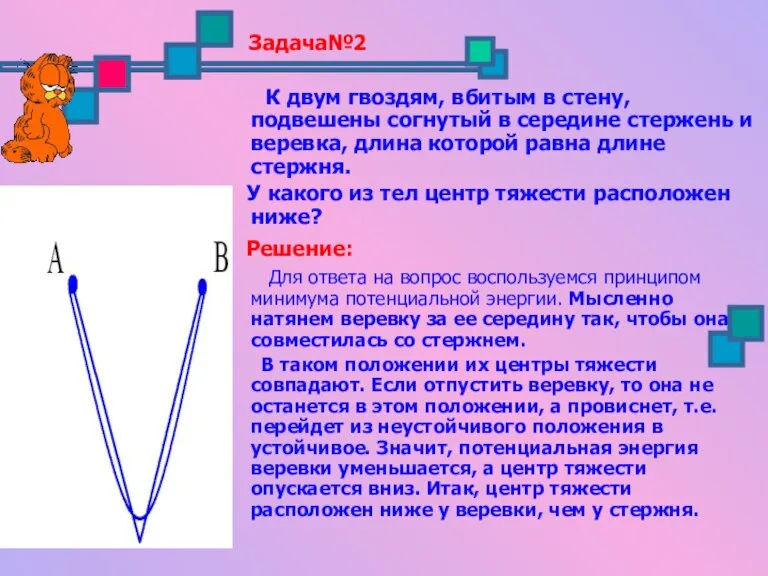
Задача№2
К двум гвоздям, вбитым в стену, подвешены согнутый в середине стержень и веревка, длина которой равна длине стержня.
У какого из тел центр тяжести расположен ниже?
Решение:
Для ответа на вопрос воспользуемся принципом минимума потенциальной энергии. Мысленно натянем веревку за ее середину так, чтобы она совместилась со стержнем.
В таком положении их центры тяжести совпадают. Если отпустить веревку, то она не останется в этом положении, а провиснет, т.е. перейдет из неустойчивого положения в устойчивое. Значит, потенциальная энергия веревки уменьшается, а центр тяжести опускается вниз. Итак, центр тяжести расположен ниже у веревки, чем у стержня.

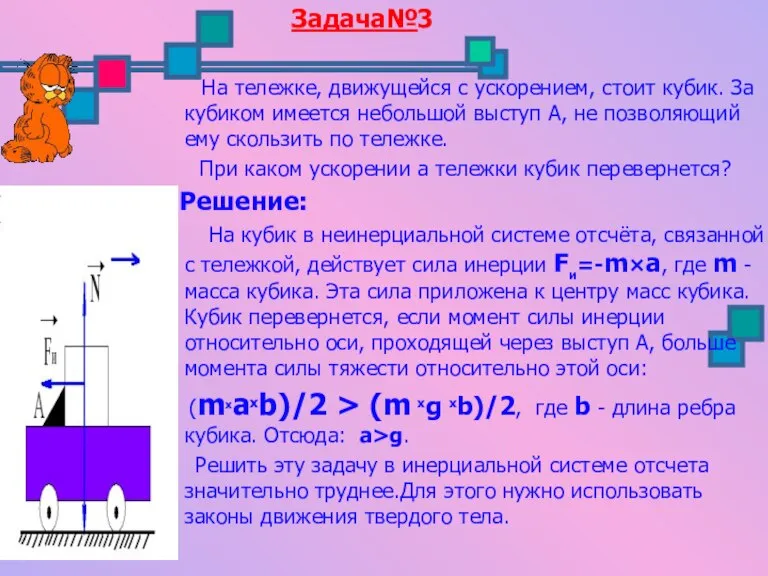
Задача№3
На тележке, движущейся с ускорением, стоит кубик. За кубиком имеется небольшой выступ А, не позволяющий ему скользить по тележке.
При каком ускорении а тележки кубик перевернется?
Решение:
На кубик в неинерциальной системе отсчёта, связанной с тележкой, действует сила инерции Fи=-m×a, где m - масса кубика. Эта сила приложена к центру масс кубика. Кубик перевернется, если момент силы инерции относительно оси, проходящей через выступ А, больше момента силы тяжести относительно этой оси:
(mхaхb)/2 > (m хg хb)/2, где b - длина ребра кубика. Отсюда: а>g.
Решить эту задачу в инерциальной системе отсчета значительно труднее.Для этого нужно использовать законы движения твердого тела.