Статистические гипотезы

Вопросы для обсуждения
Общее представление о статистических гипотезах. Статистика и параметры.
Гипотезы о среднем. Распределение Стьюдента.
Сравнение двух выборок. Структурная модель Стьюдента.
Сравнение дисперсий. F-распределение.

ВОПРОС №1
Общее представление о статистических гипотезах.

Статистическая гипотеза
Статистическая гипотеза – это предположение по поводу параметров распределения случайной величины.
Проверка статистических гипотез осуществляется путем сбора статистики.

Параметры и статистика
Параметры
Теоретическая величина характеризующая распределение случайной величины
Имеет отношение к генеральной совокупности
Практически никогда не известна
Статистика
Эмпирическая характеристика, оценка параметра распределения случайной величины
Имеет отношение к выборке
Измеряется в ходе эксперимента

Примеры гипотез

Виды гипотез
Нулевая (H0)
Утверждает что-то конкретное о параметрах распределения
Истинность определяется на основе оценки статистики
Альтернативная (H1)
Утверждает что-то противоречащее нулевой гипотезе, менее конкретна
Истинность определяется на основе рассмотрения нулевой гипотезы

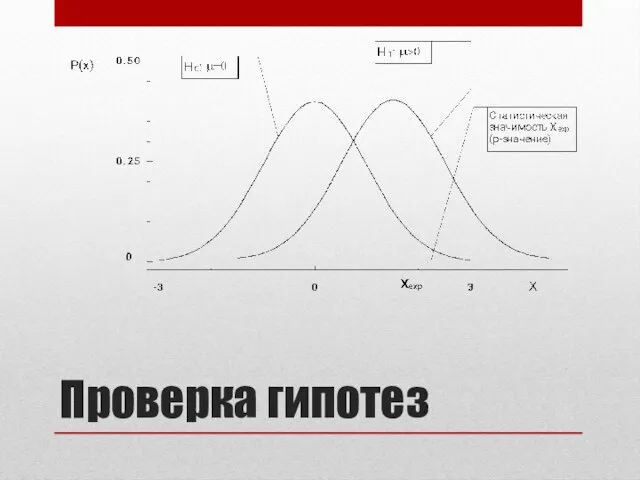
Проверка гипотез

Матрица исходов

Статистическая надежность
Теоретически не существует возможности со 100% вероятностью выбрать истинную гипотезу. Вне зависимости от установленного критерия всегда остается вероятность ошибки первого или второго рода.
Уменьшая вероятность ошибки первого рода, мы увеличиваем вероятность ошибки второго рода и наоборот.

Уровни статистической надежности

ВОПРОС №2
Гипотезы о среднем. Распределение Стьюдента.

Гипотезы о среднем
Пусть есть вектор данных X
Допустим, что X извлечены из нормальной совокупности с параметрами μ и σ2
Предположим: H0: μ=А
Тогда: H1: ≠ A

Случай №1: σ известна

Случай №2: σ неизвестна

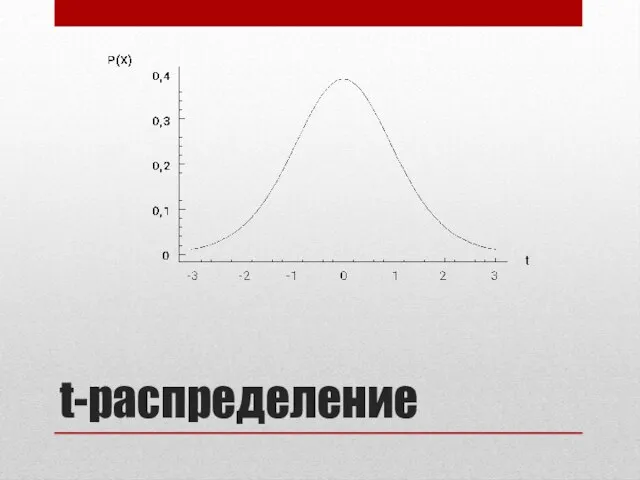
Статистика Стьюдента
Распределение t-статистики отличается от нормального.
Это распределение принято называть распределением Стьюдента, или просто t-распределением.
Распределение Стьюдента симметрично относительно среднего и имеет небольшой положительный эксцесс.
Оно характеризуется степенями свободы (обозначается df, от англ. degrees of freedom).
Для данного случая число степеней свободы t-статистики на одну меньше объема выборки, т.е. равно n-1.

t-распределение

ВОПРОС №3
Сравнение двух выборок. Структурная модель Стьюдента.

Сравнение двух выборок
Пусть есть два вектора данных – X и Y
Допустим, что X и Y извлечены из нормальной совокупности с параметрами соответственно μX и σX и μY и σY
Предположим: H0: μX = μY
Тогда: H1: μX ≠ μY

Структурная модель

Тогда…

Допустим…
Сделаем неочевидное, но правдоподобное допущение, что дисперсии X и Y одинаковы.
Поскольку дисперсии X и Y определяются дисперсией статистической ошибки ε, то

Отсюда…

ВОПРОС №4
Сравнение дисперсий. F-распределение

Сравнение дисперсий
Пусть есть два вектора данных – X и Y
Допустим, что X и Y извлечены из нормальной совокупности с параметрами соответственно μX и σX и μY и σY
Предположим: H0: σX = σY
Тогда: H1: σX ≠ σY

F-статистика

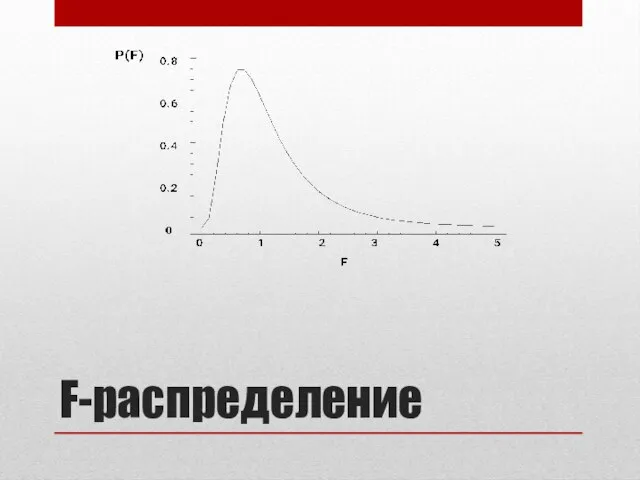
F-распределение