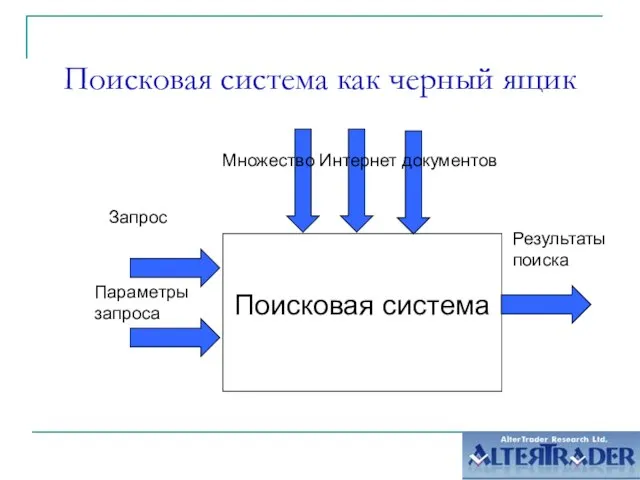
Статистические методы исследования алгоритмов текстового ранжирования поисковых систем

Поисковая система как черный ящик
Результаты поиска

Простейшие частотные метрики состава html-страниц
Абсолютная теговая частота леммы слова – количество канонических форм слова в заданном теге html-страницы.
N(L)=|L:L∈T| (1)
- количество вхождений леммы слова L в заданный тег T.
Относительная теговая частота леммы слова – отношение абсолютной теговой частоты леммы слова к общему числу лемм заданного тега html-страницы.
N%(L)=N(L)/∑N(li), li∈T (2)
Различные производные от обратной частоты документа (IDF) или обратной частоты класса ICF метрик.
IDF(L)=D/DF(L) (3),
где D-общее число документов коллекции, DF(L) - число документов, в которых встречается лемма L
ICF(L)=TCF/CF(L) (4),
где TCF-общее число лемм коллекции, CF(L) - число вхождений леммы L во все документы коллекции.

Производные от ICF/IDF метрики
IDF(L)*N(L), IDF(L)*N%(L) (5)
(6)
где li,j-все леммы j-го предложения, содержащего L, Lenj-количество слов j-го предложения.
(7)
Для каждой характеристики вместо IDF(L) можно использовать ICF(L), log(IDF(L)), log(ICF(L)). Все перечисленные выше метрики вычисляются как для каждой леммы из запроса отдельно, так и для их совокупности

Коэффициенты корреляции
Пирсона (для количественных величин)
(8),
где - математическое ожидание величины Х.
Кенделла (для ранговых величин)
(9),
где S=P-Q, P- суммарное число наблюдений, следующих за текущими наблюдениями с большим значением рангов Y, Q — суммарное число наблюдений, следующих за текущими наблюдениями с меньшим значением рангов Y
Спирмена (для ранговых величин)
(10),
где di=r(Yi)-r(Xi), r(X)-ранг Х.

Этапы исследования принципов текстового ранжирования
Этап 1. Формирования множества данных для анализа. Делается подборка запросов, максимально исключающая влияние ссылочного фактора. Например, запросы из непопулярных слов или запросы, задающие поиск по одному сайту. Чем больше различных запросов используется для проведения анализа, тем выше их статистическая значимость.
Этап 2. Вычисление числовых характеристик. Характеристики для исследования выбираются на основе проведенных предварительных наблюдений или возникающих в процессе исследования поисковых систем гипотез. В докладе представлены простейшие из них.
Этап 3. Вычисление коэффициентов корреляции. Ранговые коэффициенты вычисляются по формулам (9) или (10), а Пирсона по формуле (8), когда ранги исследуемых характеристик равны, а анализ носит сравнительный характер.
Этап 4. Анализ результатов. Если некоторая характеристика на различных запросах имеет устойчиво высокий по модулю коэффициент корреляции, то делается вывод о том, что она влияет на текстовое ранжирование.

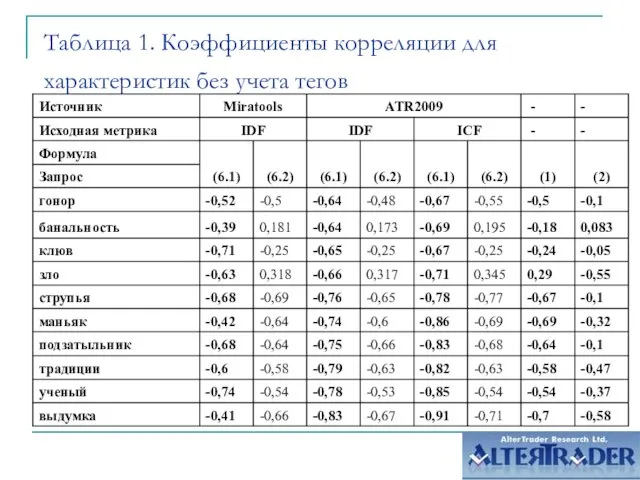
Таблица 1. Коэффициенты корреляции для характеристик без учета тегов

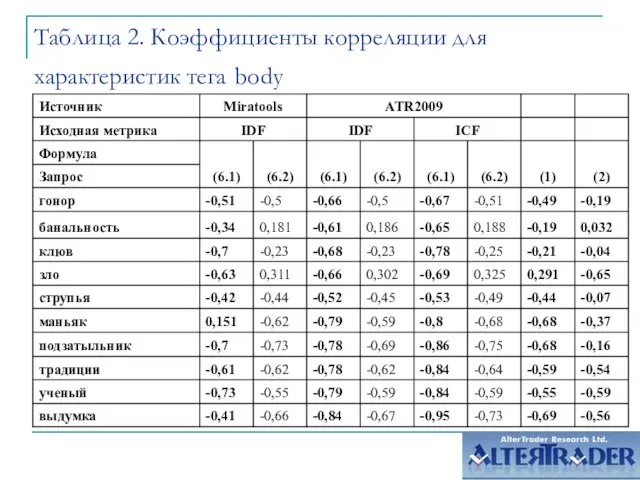
Таблица 2. Коэффициенты корреляции для характеристик тега body

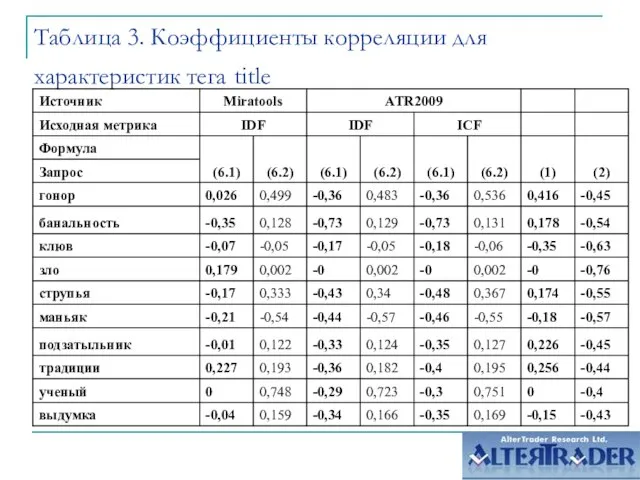
Таблица 3. Коэффициенты корреляции для характеристик тега title

Двухфакторная линейная регрессионная модель для оценивания позиции оптимизируемой страницы: Y(X1,Х2)=a2X2+a1X1+a0
Система уравнений по МНК
Решение системы