Содержание
- 2. Вопросы для обсуждения Статистические основы внутригруппового эксперимента. Однофакторный дисперсионный анализ с повторным измерением. Структурные модели однофакторного
- 3. ВОПРОС №1 Внутригрупповой эксперимент…
- 4. Внутригрупповой план В отличие от межгруппового плана внутригрупповой экспериментальных план предполагает использование всего одной группы испытуемых
- 5. Повторные измерения
- 6. Анализ дисперсии
- 7. Между испытуемыми
- 8. Внутри испытуемых
- 9. Экспериментальное воздействие
- 10. Остаток
- 11. Всего
- 12. Оценка дисперсии
- 13. F-отношение
- 14. ВОПРОС №2 Структурная модель однофакторного дисперсионного анализа с повторным измерением
- 15. Структурная модель
- 16. Допущения Экспериментальная ошибка представляет собой случайную величину, распределенную в соответствии с нормальным законом с математическим ожиданием
- 17. Модель I
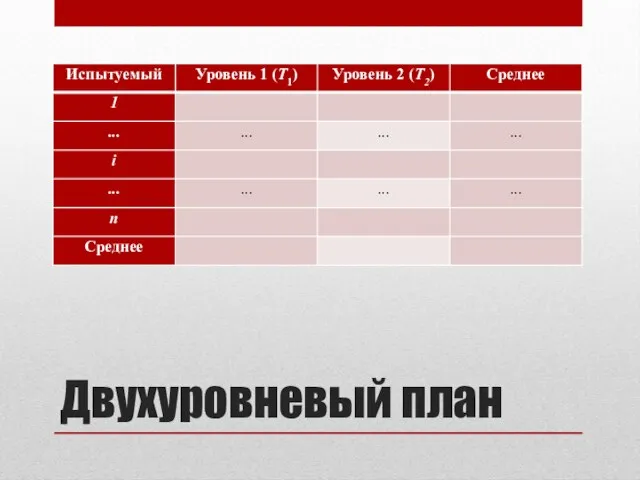
- 18. Двухуровневый план
- 19. Дисперсия ЗП для каждого уровня НП Поскольку величины μ, τ1 и τ2 постоянны, дисперсия внутри экспериментального
- 20. Тогда… Величины σ2ε являются статистически независимыми друг от друга в двух экспериментальных условиях, чего нельзя сказать
- 21. Следовательно…
- 22. Модель I: гипотезы Нулевая - H0 Альтернативная – H1
- 23. Модель II
- 24. Тогда…
- 25. Модель II: гипотезы Нулевая - H0 Альтернативная – H1
- 26. Многоуровневый план где μj – математическое ожидание значения зависимой переменной на уровне j Тогда ковариация значений
- 27. Однородность матрицы ковариаций Поскольку, согласно предположению модели, эффект испытуемого не взаимодействует с эффектами независимой переменной, матрица
- 28. Тогда… Оценка дисперсии для одного экспериментального условия
- 29. Наконец…
- 30. Гипотезы Нулевая - H0 Альтернативная – H1
- 31. Оценка однородности ковариаций Для оценки однородности ковариационной матрицы используют тест сферичности Моучли (Mauchly). Если этот тест
- 32. Уменьшение df
- 34. Скачать презентацию






























 ДЕПАРТАМЕНТ образования ГОРОДА МОСКВЫМОСКОВСКИЙ ГОРОДСКОЙ ПСИХОЛОГО-ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ
ДЕПАРТАМЕНТ образования ГОРОДА МОСКВЫМОСКОВСКИЙ ГОРОДСКОЙ ПСИХОЛОГО-ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ Святая Екатерина Александрийская
Святая Екатерина Александрийская Summer memory game
Summer memory game Defining Culture
Defining Culture RPM 89. Образовательная сессия
RPM 89. Образовательная сессия Экосистема леса Лесные кустарники и травы
Экосистема леса Лесные кустарники и травы Спостереження за моїм собакою
Спостереження за моїм собакою Предприятие ООО «Квантсервер» известно на рынке Алтайского края и других регионов России как ведущий поставщик кукурузных палоче
Предприятие ООО «Квантсервер» известно на рынке Алтайского края и других регионов России как ведущий поставщик кукурузных палоче 2. Сущность права
2. Сущность права Презентация на тему Характеристика стран НИС
Презентация на тему Характеристика стран НИС  Общая физическая подготовка. Развитие всех физических качеств (сила, выносливость, координации, скорость, ловкость, гибкость)
Общая физическая подготовка. Развитие всех физических качеств (сила, выносливость, координации, скорость, ловкость, гибкость)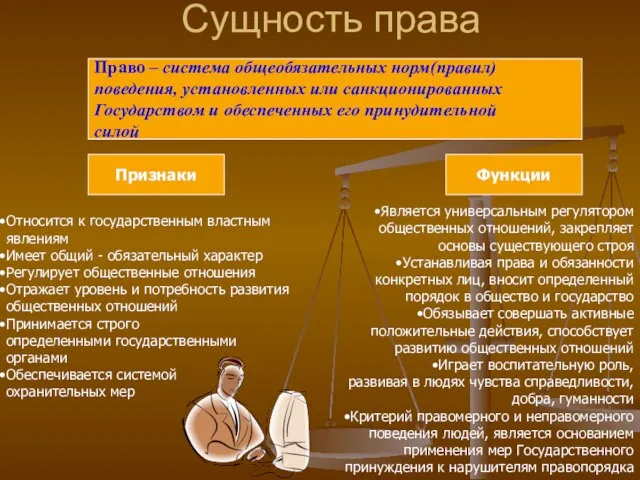 Сущность права
Сущность права Школьникам о правильном питании
Школьникам о правильном питании Лягушачье золото
Лягушачье золото НА ПРОСТОРАХ
НА ПРОСТОРАХ Стихотворения М.Ю.Лермонтова «Три пальмы», «Листок», «Утёс»
Стихотворения М.Ю.Лермонтова «Три пальмы», «Листок», «Утёс» Презентацияпо темеОтдел Папоротникообразные.
Презентацияпо темеОтдел Папоротникообразные. NEW YORK CITY
NEW YORK CITY  Герб
Герб Презентация к интеллектуальной игре «Конституция – главный арбитр государства»(по Конституции 1993г.) Подготовила: Варюхина Римм
Презентация к интеллектуальной игре «Конституция – главный арбитр государства»(по Конституции 1993г.) Подготовила: Варюхина Римм Вашему вниманию предлагается новая система в MainLink «Быстрый старт», которая позволяет запустить продвижение сайта по одному или бо
Вашему вниманию предлагается новая система в MainLink «Быстрый старт», которая позволяет запустить продвижение сайта по одному или бо О полезных ископаемых и первых железных дорогах
О полезных ископаемых и первых железных дорогах полная и краткая форма
полная и краткая форма Напольный светильник "Семейный очаг"
Напольный светильник "Семейный очаг" С масленицей. Готовка блинов
С масленицей. Готовка блинов Возвращение блудного сына Рембрандта
Возвращение блудного сына Рембрандта История Российского Флага
История Российского Флага Волшебные ленты
Волшебные ленты