СТАТИСТИКА.

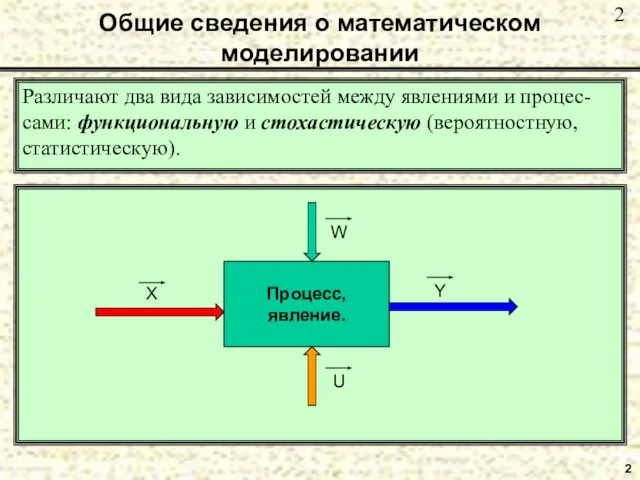
2
Общие сведения о математическом моделировании
Различают два вида зависимостей между явлениями и процес-сами: функциональную и стохастическую (вероятностную, статистическую).

3
Моделирование рядов распределения
Если имеется эмпирический ряд распределения, то необходимо найти функцию распределения, т.е. подобрать такую теоретическую кривую распределения, которая наиболее полно отображала бы закономер-ность распределения. Нахождение функции кривой распределения на-зывается моделированием эмпирического ряда распределения.

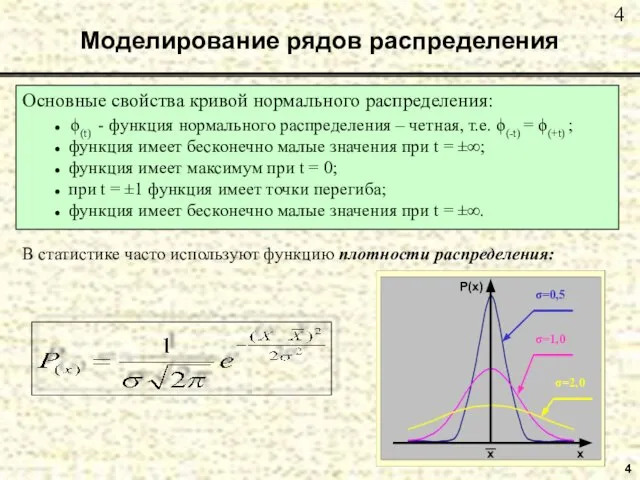
4
Моделирование рядов распределения
Основные свойства кривой нормального распределения:
● ϕ(t) - функция нормального распределения – четная, т.е. ϕ(-t) = ϕ(+t) ;
● функция имеет бесконечно малые значения при t = ±∞;
● функция имеет максимум при t = 0;
● при t = ±1 функция имеет точки перегиба;
● функция имеет бесконечно малые значения при t = ±∞.

5
Моделирование рядов распределения
Связь между теоретической нормированной функцией нормального распределения и теоретической денормированной функцией нормального распределения для интервального вариационного ряда определяется соот-ношением:
где А – коэффициент нормировки, который для распределения с равными интервалами Δx=k рассчитывается с помощью соотношения:
fi - частота i-го интервала ряда.

6
Расчет теоретических частот нормального распределения
Пример. В приведенной таблице показано распределение ткачих по степени выполнения норм выработки. Исходя из предположения о нормальном законе распределения определить теоретические частоты.

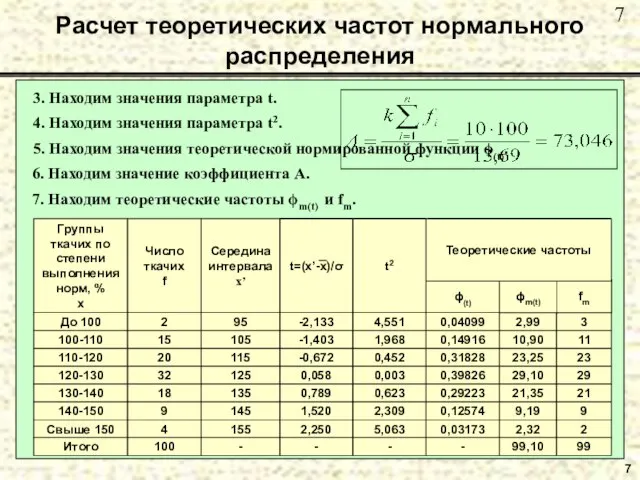
7
Расчет теоретических частот нормального распределения
3. Находим значения параметра t.
4. Находим значения параметра t2.
5. Находим значения теоретической нормированной функции ϕ(t).
6. Находим значение коэффициента А.
7. Находим теоретические частоты ϕm(t) и fm.

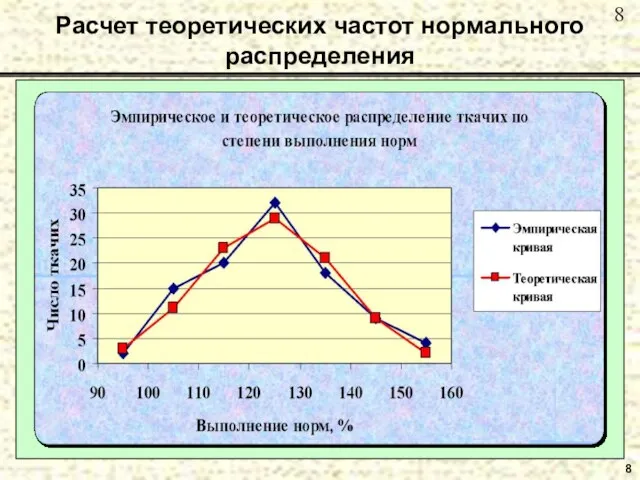
8
Расчет теоретических частот нормального распределения

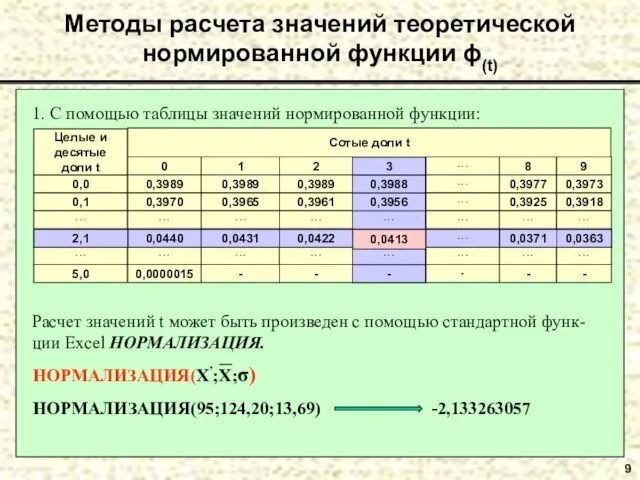
9
Методы расчета значений теоретической нормированной функции ϕ(t)
1. С помощью таблицы значений нормированной функции:

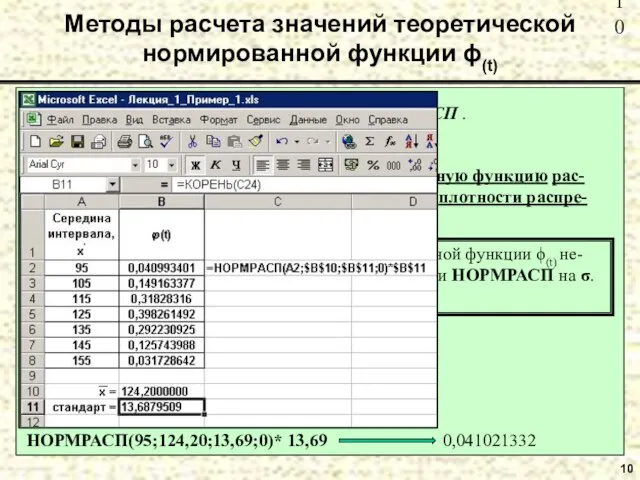
10
Методы расчета значений теоретической нормированной функции ϕ(t)
2. С помощью стандартной функции Excel НОРМРАСП .
Для получения значений теоретической нормированной функции ϕ(t) не-обходимо домножить возвращаемое значение функции НОРМРАСП на σ.

11
Критерий согласия Пирсона
Критерий согласия Пирсона:
Для найденного значения критерия согласия Пирсона и числа степеней свободы γ=n-1 определяется соответствующая вероятность P(χ2).
При P(χ2)>0,5 считается, что эмпирическое и теоретическое распределе-ния близки, при P(χ2)∈[0,2;0,5] совпадение удовлетворительное, в осталь-ных случаях – недостаточное.

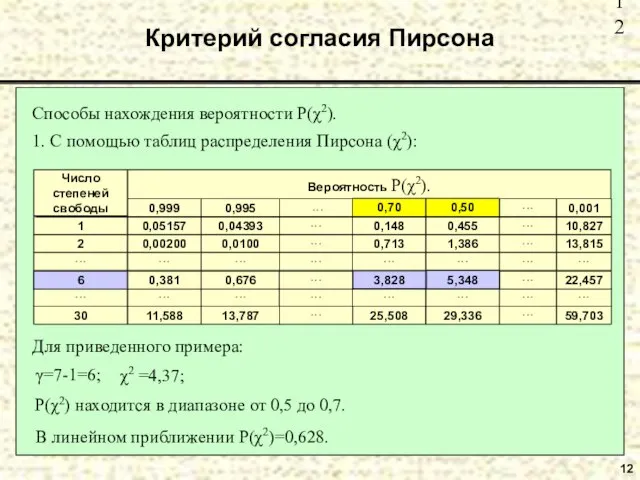
12
Критерий согласия Пирсона
Способы нахождения вероятности P(χ2).
В линейном приближении Р(χ2)=0,628.

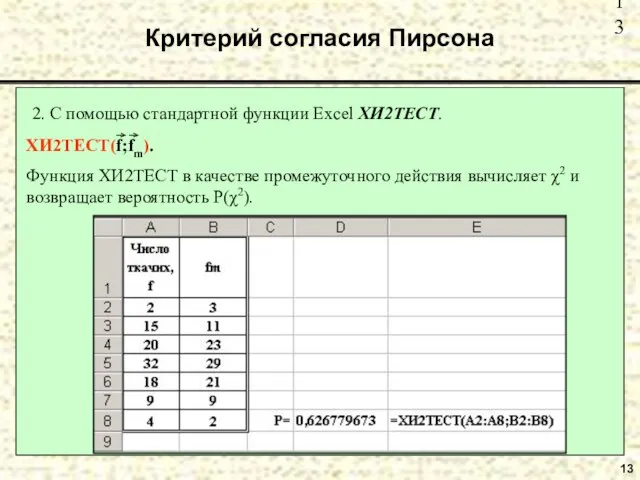
13
Критерий согласия Пирсона
2. С помощью стандартной функции Excel ХИ2ТЕСТ.

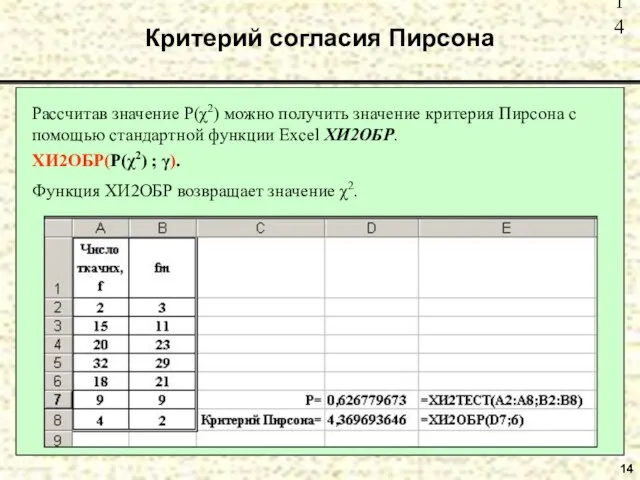
14
Критерий согласия Пирсона
Рассчитав значение P(χ2) можно получить значение критерия Пирсона с помощью стандартной функции Excel ХИ2ОБР.
ХИ2ОБР(P(χ2) ; γ).
Функция ХИ2ОБР возвращает значение χ2.

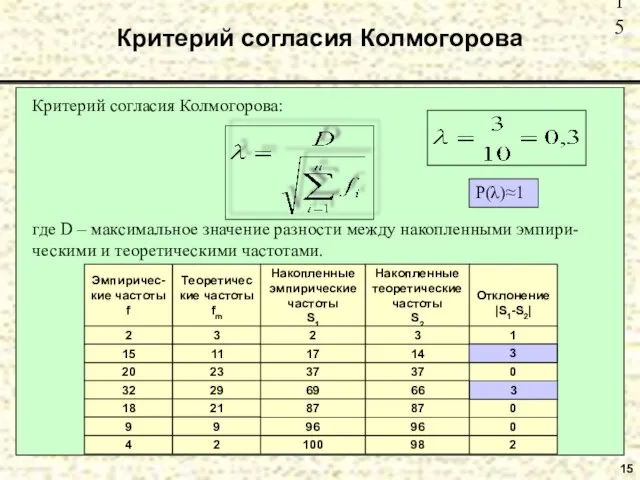
15
Критерий согласия Колмогорова
Критерий согласия Колмогорова:
где D – максимальное значение разности между накопленными эмпири-ческими и теоретическими частотами.