Стратегия игр

Теория игр - раздел математики
исследующий вопросы поведения участников игры
разрабатывающий оптимальные стратегии поведения каждого из участников игры

Простейшие математические игры - это
задачи, в которых нужно найти выигрышную стратегию
либо одно положение перевести в другое.

Что такое игровая, стратегическая задача?
в ней часто нет ничего числового
иногда в играх нельзя придумать алгоритм победы , в игре возможна победа и без стратегии, а также ничья

Цель работы:
изучить новые методы решения нестандартных задач,
попробовать вывести «правила» решения некоторых игровых задач,
расширить свои знания по математике.

Методы решения игровых задач
Инвариант
Стратегия - четность
Раскраска
Стратегия - чередование состояний
Симметрия
Стратегия - повтор ходов противника

Виды игровых задач по способам решений
Игры-шутки.
Игры, использующие симметрию.
Игры, в которых стратегия — дополнение до фиксированного числа.
Игры, использующие метод выигрышных позиций

1. Игры-шутки.
Двое по очереди ломают шоколадку 5x8. За ход можно разломать любой кусок по прямой линии между дольками. Проигрывает тот, кто не может сделать ход. Кто выиграет при правильной игре?
Если число кусочков шоколадки четно, тогда побеждает первый, если число нечетно, тогда второй.

2. Симметрия (осевая).
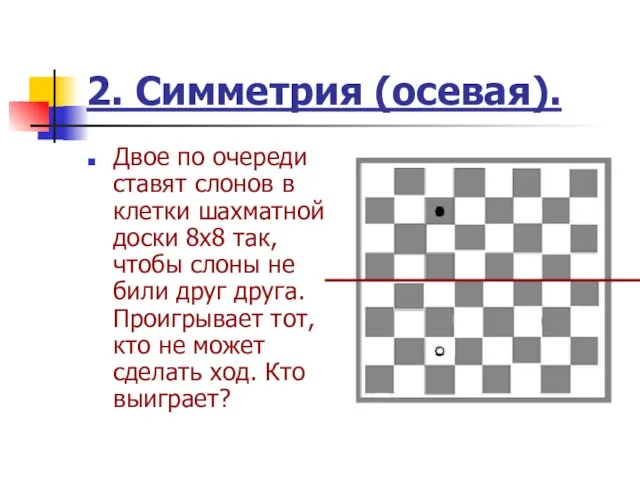
Двое по очереди ставят слонов в клетки шахматной доски 8x8 так, чтобы слоны не били друг друга. Проигрывает тот, кто не может сделать ход. Кто выиграет?

Задача 2.
Двое играют, поочередно выставляя крестики и нолики на квадратном поле 9х9. В конце каждый получает очко за каждую строку и столбец, в которых его знаков больше. Сможет ли первый игрок выиграть?

Стратегия – центральная симметрия

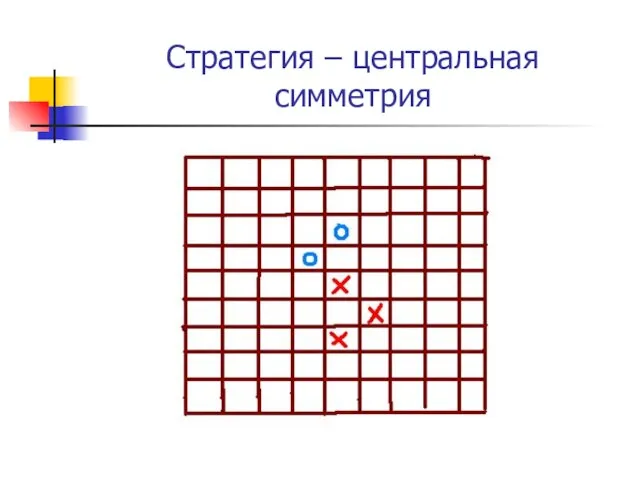
3. Игры, в которых стратегия — дополнение до фиксированного числа.
Двое играют в игру. Ходы, которые делаются по очереди, заключаются в том, что из кучки в 50 камней убирается любое число камней от 1 до 5. Выигрывает тот, кто возьмет последний камень. Кто выиграет в данной игре?

Метод малых задач
Меньше 5 камней – выигрыш 1
6 камней – выигрыш 2
7 камней – выигрыш 1
8 камней – выигрыш 1
12 камней – выигрыш 2
Если делится на 6 – выигрыш 2
если нет – выигрыш 1

Стратегия игры
Может выиграть 1, если он возьмет:
2 камня, оставляя 48 камней (1 ход)
Каждый следующий ход соперника он должен дополнить до 6 камней.
Выиграет – начинающий.

4. Вспомогательные раскраски в шахматном порядке.
Доску размером 10х10 клеток разрезать на фигурки в форме буквы Т, состоящие из четырех клеток.

Метод – раскраска
Стратегия - четность
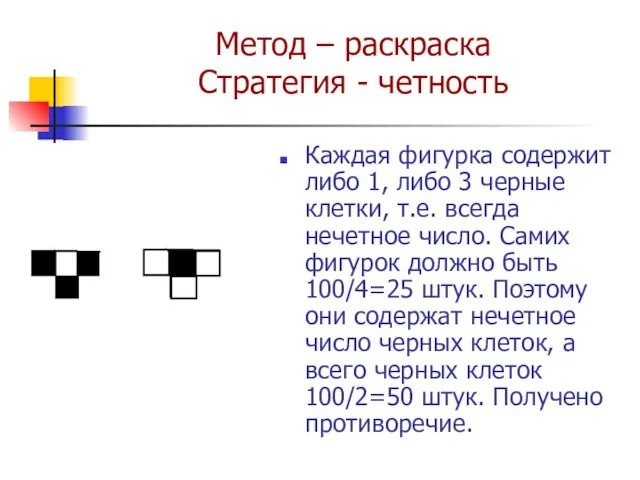
Каждая фигурка содержит либо 1, либо 3 черные клетки, т.е. всегда нечетное число. Самих фигурок должно быть 100/4=25 штук. Поэтому они содержат нечетное число черных клеток, а всего черных клеток 100/2=50 штук. Получено противоречие.

Выводы:
игровые задачи являются одним из самых мощных инструментов развития человеческого интеллекта,
эти задачи проверяют не знания, а умение логически рассуждать, ориентироваться в необычных ситуациях, предвидеть и действовать.

Известный русский математик В.П. Ермаков говорил: «В математике следует помнить не формулы, а процесс мышления ». Это демонстрируют задачи с играми.