Содержание
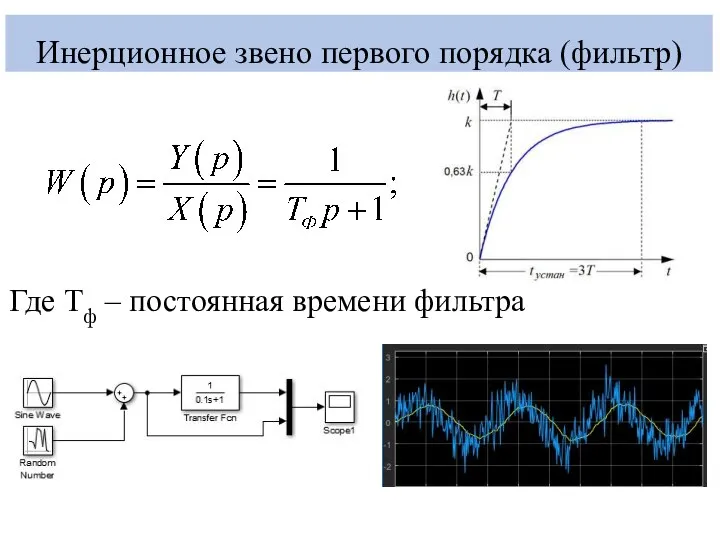
- 2. Инерционное звено первого порядка (фильтр) Где Тф – постоянная времени фильтра
- 3. Пример разработки и отладки программы инерционного звена первого порядка (фильтра) Для преобразования уравнения фильтра из непрерывной
- 4. Пример разработки и отладки программы инерционного звена первого порядка (фильтра)
- 5. Пример разработки и отладки программы инерционного звена первого порядка (фильтра) void Filter_Init() { ky1=_IQdiv(Th,Th+_IQ(1)); kx0=_IQdiv(_IQ(1),Th+_IQ(1)); }
- 6. Пример разработки и отладки программы инерционного звена первого порядка (фильтра) Можно принять допущение и упростить формулы:
- 7. Пример разработки и отладки программы инерционного звена первого порядка (фильтра) Упрощенное выражение фильтра Это выражение имеет
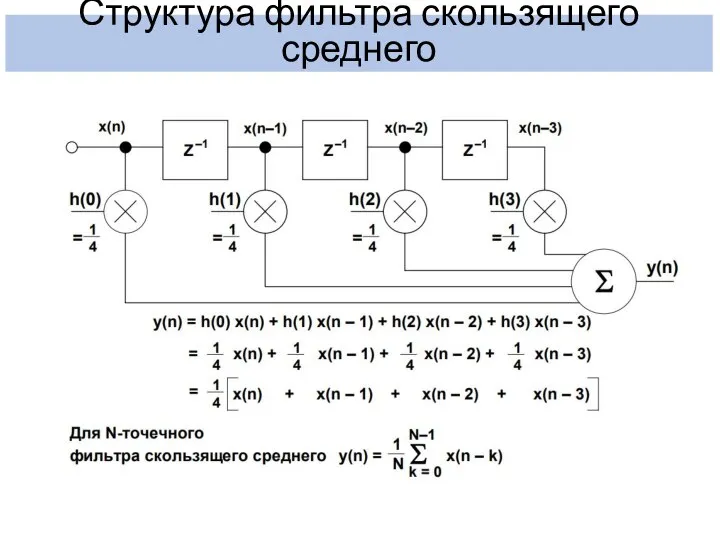
- 8. Структура фильтра скользящего среднего
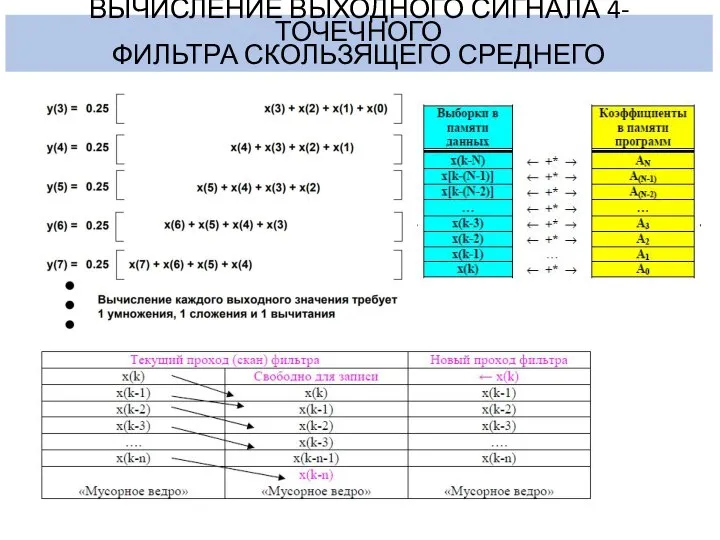
- 9. ВЫЧИСЛЕНИЕ ВЫХОДНОГО СИГНАЛА 4-ТОЧЕЧНОГО ФИЛЬТРА СКОЛЬЗЯЩЕГО СРЕДНЕГО
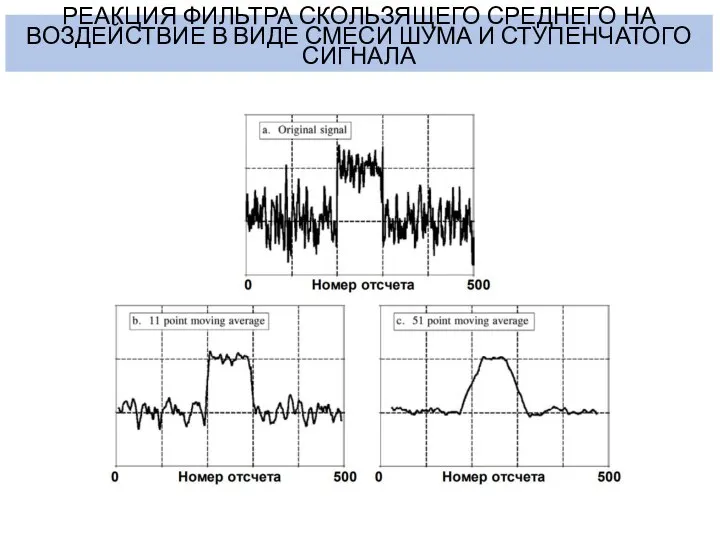
- 10. РЕАКЦИЯ ФИЛЬТРА СКОЛЬЗЯЩЕГО СРЕДНЕГО НА ВОЗДЕЙСТВИЕ В ВИДЕ СМЕСИ ШУМА И СТУПЕНЧАТОГО СИГНАЛА
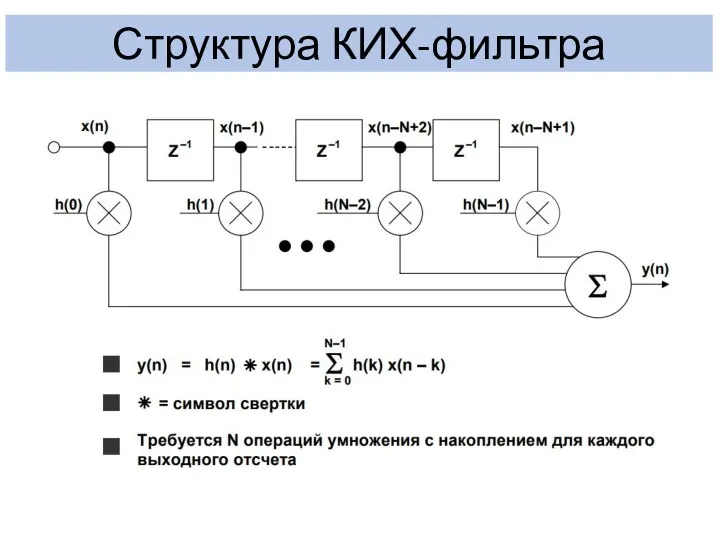
- 11. Структура КИХ-фильтра
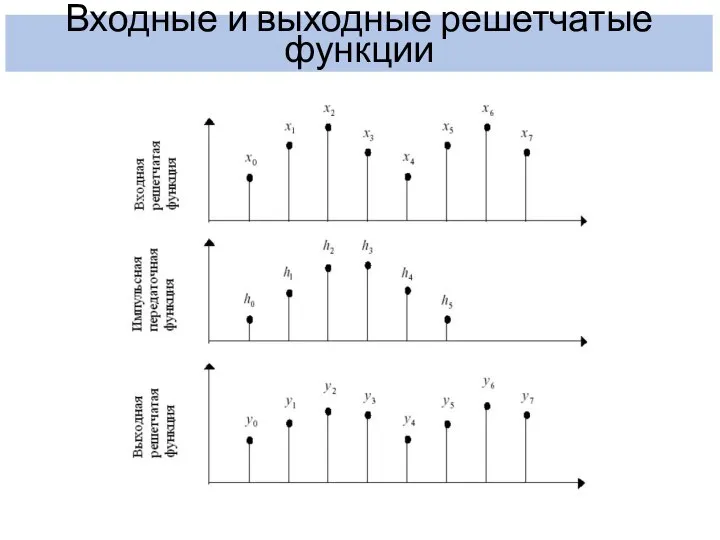
- 12. Входные и выходные решетчатые функции
- 13. ХАРАКТЕРИСТИКИ КИХ-ФИЛЬТРОВ Выходное управляющее воздействие (результат работы фильтра) представляет собой сумму произведений величин, сохраненных в линии
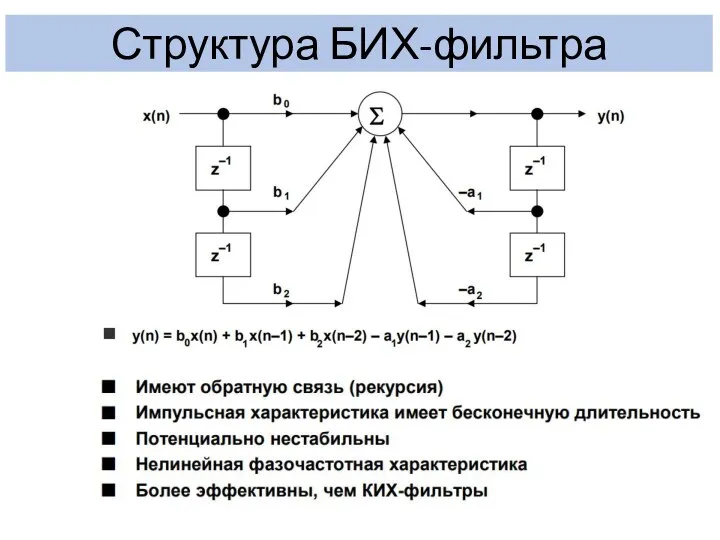
- 14. Структура БИХ-фильтра
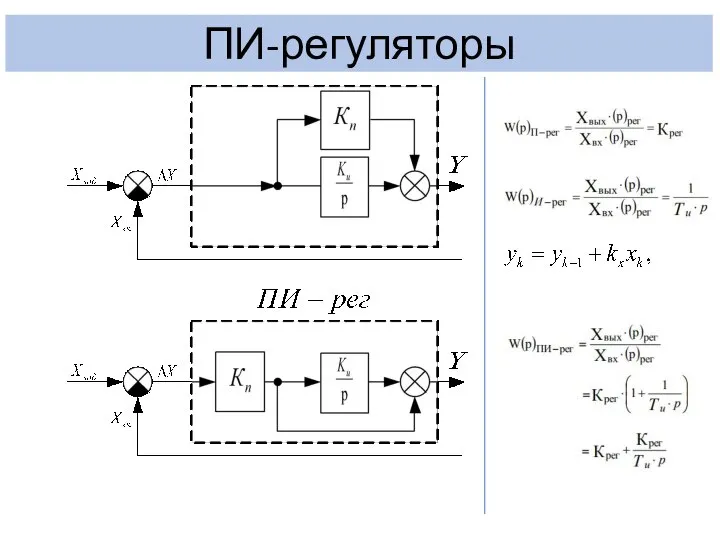
- 15. ПИ-регуляторы
- 17. Скачать презентацию






 khim_sost
khim_sost Болезни органов слуха и зрения
Болезни органов слуха и зрения Кружево листьев
Кружево листьев жизнь экосистемы
жизнь экосистемы Ресурсы для организации технологического, инженерно-технического, направления в современной школе
Ресурсы для организации технологического, инженерно-технического, направления в современной школе Презентация на тему Значение воды на Земле
Презентация на тему Значение воды на Земле Технологические потребности предприятий электронной промышленности Российская электроника Алексей Борисович Данилин Руководит
Технологические потребности предприятий электронной промышленности Российская электроника Алексей Борисович Данилин Руководит Типы поведения в группах и лидерство
Типы поведения в группах и лидерство Психологические факторы и механизмы нарушений восприятия
Психологические факторы и механизмы нарушений восприятия Презентация на тему Точка, прямая, отрезок, луч и угол (7 класс)
Презентация на тему Точка, прямая, отрезок, луч и угол (7 класс) Арбитражные аппеляционные суды Выполнила студентка 1 курса юридического факультета Группа 1405 Николаева Дарья
Арбитражные аппеляционные суды Выполнила студентка 1 курса юридического факультета Группа 1405 Николаева Дарья Правовая охрана программ и данных. Защита информации
Правовая охрана программ и данных. Защита информации Основные задачи проекта благоустройства:
Основные задачи проекта благоустройства: Цветаева Марина Ивановна
Цветаева Марина Ивановна Презентация на тему Ландшафтный дизайн
Презентация на тему Ландшафтный дизайн LODGER
LODGER Компьютерные презентации
Компьютерные презентации Архипелаг Кронштадт
Архипелаг Кронштадт Презентация на тему Природные источники углеводородов
Презентация на тему Природные источники углеводородов  проекты вк
проекты вк Объекты и их имена
Объекты и их имена Определение «блага» и классификация
Определение «блага» и классификация Пейзажная лирика А.С. Пушкина
Пейзажная лирика А.С. Пушкина Признаки реакций
Признаки реакций Идеи по рукоделию
Идеи по рукоделию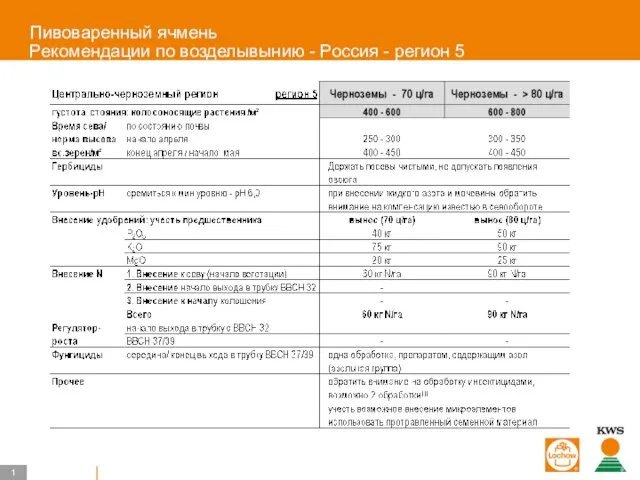 Пивоваренный ячмень Рекомендации по возделывынию - Россия - регион 5
Пивоваренный ячмень Рекомендации по возделывынию - Россия - регион 5 Виды жилых помещений (5 класс)
Виды жилых помещений (5 класс) Презентация на тему Станционный смотритель
Презентация на тему Станционный смотритель