Содержание
- 2. Основные свойства функции у =sinх: Область определения- множество всех действительных чисел; Область значения- отрезок [-1;1], значит,
- 3. sinx= 0 при х=∏n, n є Z; sinx > 0 для всех х є (2∏n; ∏+2∏n),n
- 4. Функция возрастает от -1 до 1 на промежутках [-∏/2 + 2∏n; ∏/2 + 2∏n], n є
- 5. График cинуса на промежутке [-∏;∏]
- 6. График синуса на всей области определения
- 7. Построить график функции y=sin 1/2x D (y)= R; E (y)= [-1;1]; Функция нечётная; Функция периодическая, так
- 8. Найдём точки пересечения графика с осью ОХ. Если y=0, то sin1/2 x=0, х/2=∏n, х=2∏n, n=0;1. (0;0)
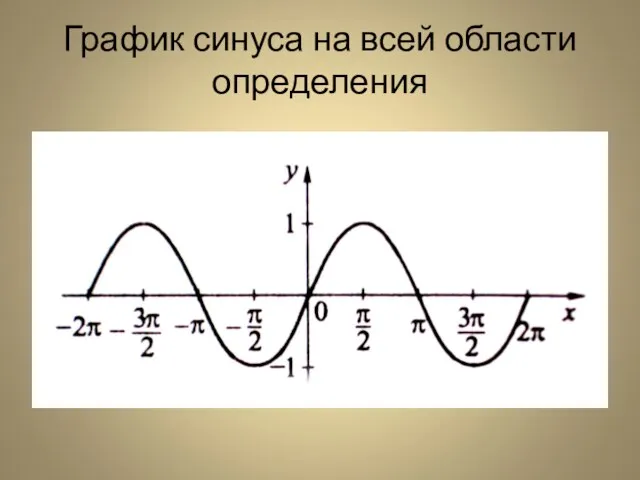
- 9. График функции y=sin1/2x
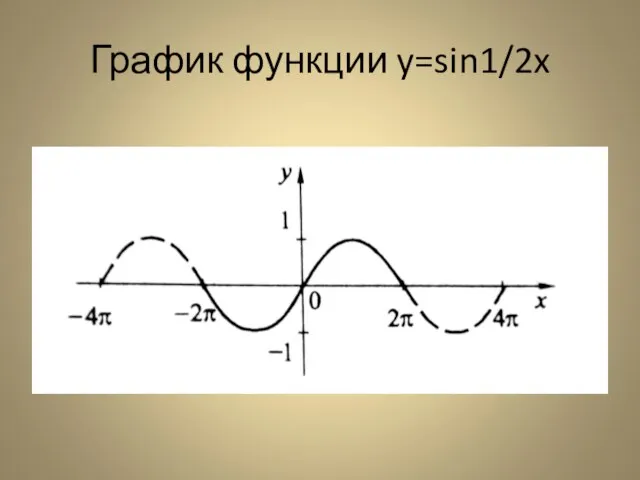
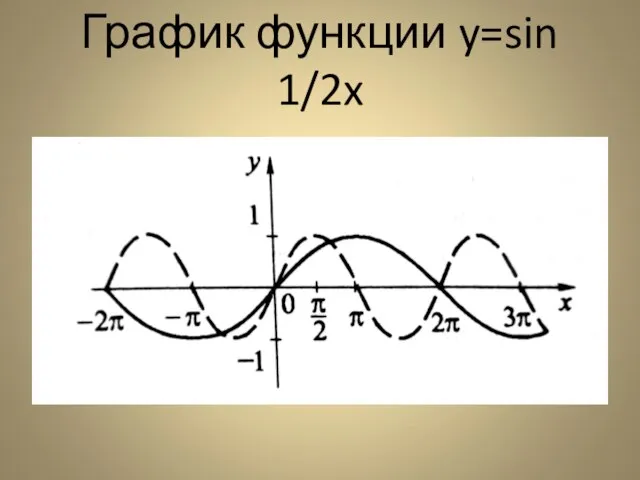
- 10. Второй способ построения графика функции y=sin 1/2x Период исходной функции y=sinx равен 2∏, а период заданной
- 11. График функции y=sin 1/2x
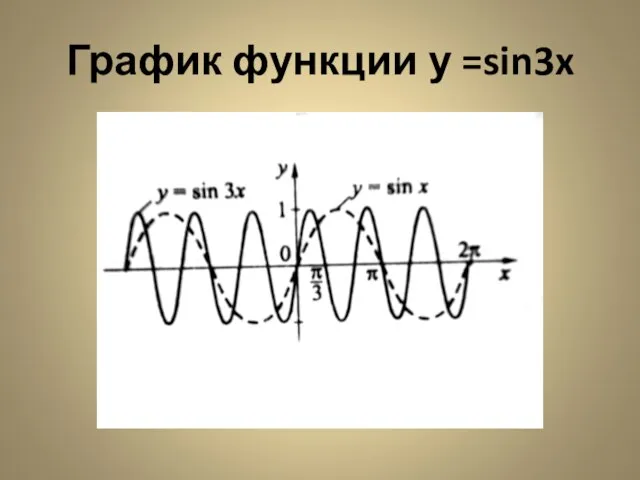
- 12. Построить график функции y=sin3x D(y)=R; E(Y)=[-1;1]; Период функции: Sin3x= sin (3x + 2∏) = sin3(x+2∏/3); T=2∏/3,
- 13. График функции y=sin3x
- 14. Второй способ построения графика функции у= sin3x График функции у=sin3x можно построить путём сжатия по оси
- 15. График функции у =sin3x
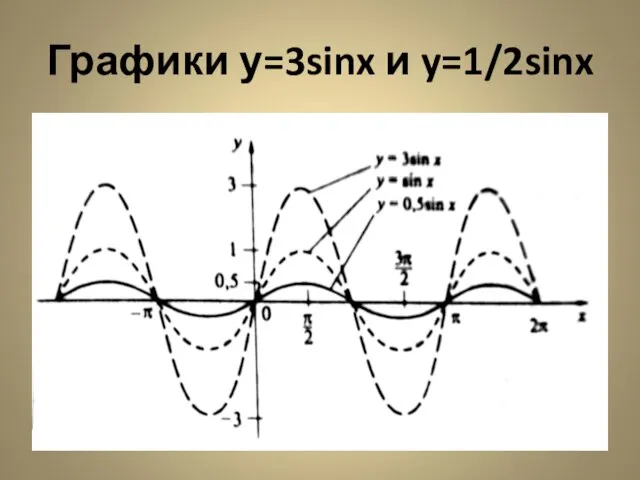
- 16. Построить график функции y=3sinx Ординаты графика y=3sinx в три раза больше соответствующих ординат графика y=sinx. Поэтому
- 17. Построить график функции у=1/2sinx По тем же соображениям этот график строится способом уменьшения всех ординат исходного
- 18. Графики у=3sinx и y=1/2sinx
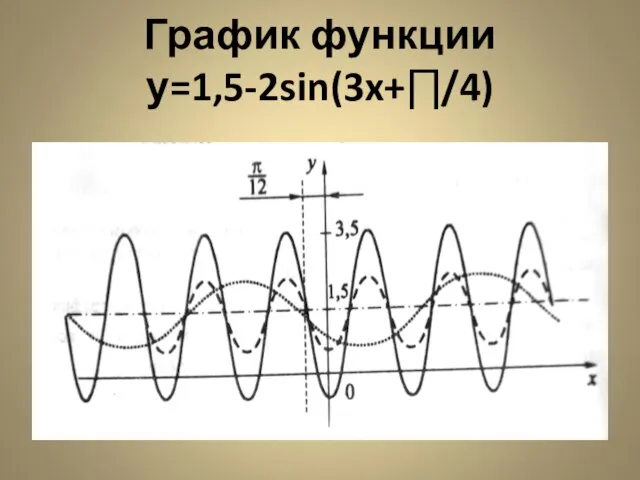
- 19. Построить график функции у=1,5-2sin(3x+∏/4) Y= -2sin(3x+∏/4) Y= -2sin(3(x+∏/12))+1,5 Порядок построения графика следующий: строим график функции y=-sinx;
- 20. График функции у=1,5-2sin(3x+∏/4)
- 21. Упражнения для самостоятельной работы Первый вариант Построить графики функций: 1. y=sin2x; 2. y= 1-2sin2x; y= 2sinxlcosxl;
- 23. Скачать презентацию

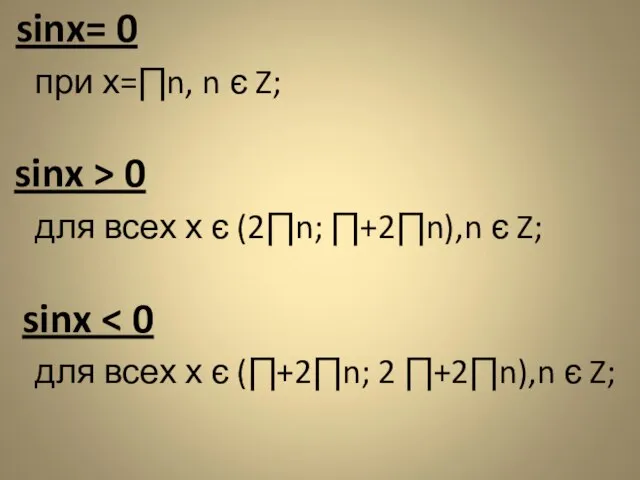

![График cинуса на промежутке [-∏;∏]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/433767/slide-4.jpg)
![Построить график функции y=sin 1/2x D (y)= R; E (y)= [-1;1]; Функция](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/433767/slide-6.jpg)


![Построить график функции y=sin3x D(y)=R; E(Y)=[-1;1]; Период функции: Sin3x= sin (3x +](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/433767/slide-11.jpg)






 Рейтинг популярности услуг аутсорсинга среди иностранных компаний, представленных в России Совместный проект аутсорсингового п
Рейтинг популярности услуг аутсорсинга среди иностранных компаний, представленных в России Совместный проект аутсорсингового п Разработка стратегии развертывания приложений
Разработка стратегии развертывания приложений Собственная и примесная проводимость полупроводников
Собственная и примесная проводимость полупроводников  Презентация на тему Развитие жизни в палеозойской эре Ранний палеозой (кембрий, ордовик, силур)
Презентация на тему Развитие жизни в палеозойской эре Ранний палеозой (кембрий, ордовик, силур)  Расчеты по уравнениям реакций, протекающих в растворах
Расчеты по уравнениям реакций, протекающих в растворах Презентация на тему Моя снежинка не растает
Презентация на тему Моя снежинка не растает Календарь-трансформер
Календарь-трансформер Становись партнером и зарабатывай с продажи билетов
Становись партнером и зарабатывай с продажи билетов Типовые приемы в консультировании
Типовые приемы в консультировании Презентация на тему Одежда Средних веков (5 класс)
Презентация на тему Одежда Средних веков (5 класс) Презентация на тему Военные года 1941-1945
Презентация на тему Военные года 1941-1945  Принципы осуществления радиосвязи
Принципы осуществления радиосвязи ООО Алми. Строительная компания
ООО Алми. Строительная компания Алиаскарова Ж.А. Человек науки
Алиаскарова Ж.А. Человек науки Стили речи. Введение в стилистику
Стили речи. Введение в стилистику Исследование и разработка направленного ответвителя с улучшенными характеристиками
Исследование и разработка направленного ответвителя с улучшенными характеристиками Auto Lux. Расширяем возможности микс системы. Набор специальных пигментов от кампании Примо Колор
Auto Lux. Расширяем возможности микс системы. Набор специальных пигментов от кампании Примо Колор СБЕРБАНК ЛИЗИНГ НОВЫЕ ВОЗМОЖНОСТИСЕГОДНЯ
СБЕРБАНК ЛИЗИНГ НОВЫЕ ВОЗМОЖНОСТИСЕГОДНЯ Призер муниципального этапа всероссийской олимпиады школьников по физической культуре Бушковский Никита
Призер муниципального этапа всероссийской олимпиады школьников по физической культуре Бушковский Никита Уважаемые коллеги! От имени коллектива НП Национальная страховая гильдия » примите искренние поздравления с профессиональным
Уважаемые коллеги! От имени коллектива НП Национальная страховая гильдия » примите искренние поздравления с профессиональным  Конспект занятия по развитию речив подготовительной группе детского сада на тему: «Музей почтовых принадлежностей» (с использов
Конспект занятия по развитию речив подготовительной группе детского сада на тему: «Музей почтовых принадлежностей» (с использов Функции русского языка в современном мире
Функции русского языка в современном мире Семейный очаг
Семейный очаг Александр Александрович Блок
Александр Александрович Блок О внедрении системы электронного общения с родителями 10 а класса МОУ СОШ №17 классного руководителя Печкуровой Е.А
О внедрении системы электронного общения с родителями 10 а класса МОУ СОШ №17 классного руководителя Печкуровой Е.А Мотивация и стимулирование труда персонала в государственном учреждении КГБОУ Барнаульская общеобразовательная школа-интернат №3
Мотивация и стимулирование труда персонала в государственном учреждении КГБОУ Барнаульская общеобразовательная школа-интернат №3 Проектирование технологического процесса на изготовление детали чашка каретки левая с годовой программой выпуска 40000 штук
Проектирование технологического процесса на изготовление детали чашка каретки левая с годовой программой выпуска 40000 штук Портреты великих исполнителей
Портреты великих исполнителей