Содержание
- 2. Построение графика функции, заданной формулой, начинают с её исследования 1) Находят область определения функции 2) Выясняют,
- 3. Промежутки возрастания и убывания (промежутки монотонности). Достаточный признак убывания : если f’ (x) 0, то f
- 4. Пример. Для функции найти промежутки монотонности. D(f)=( –∞; +∞), функция непрерывна и дифференируема на области определения.
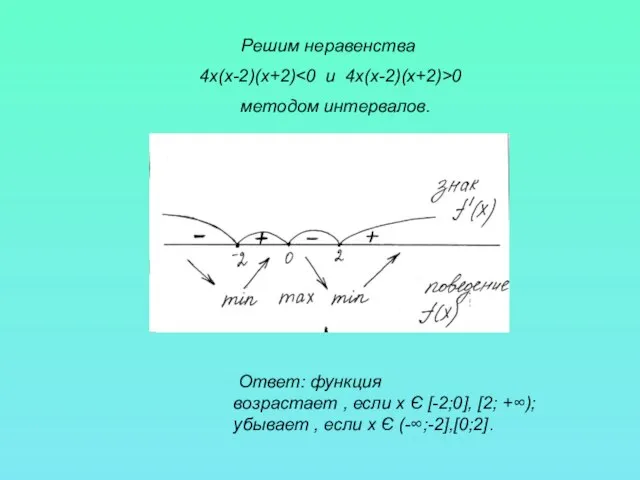
- 5. Решим неравенства 4х(х-2)(х+2) 0 методом интервалов. Ответ: функция возрастает , если х Є [-2;0], [2; +∞);
- 6. Точки экстремума функции (точки максимума и точки минимума) Точка a называется точкой максимума функции f(x), если
- 7. Точки экстремума функции (точки максимума и точки минимума) Точка a называется точкой минимума функции f(x), если
- 8. Если производная сохраняет свой знак при переходе через точку a, то такая точка называется точкой перегиба
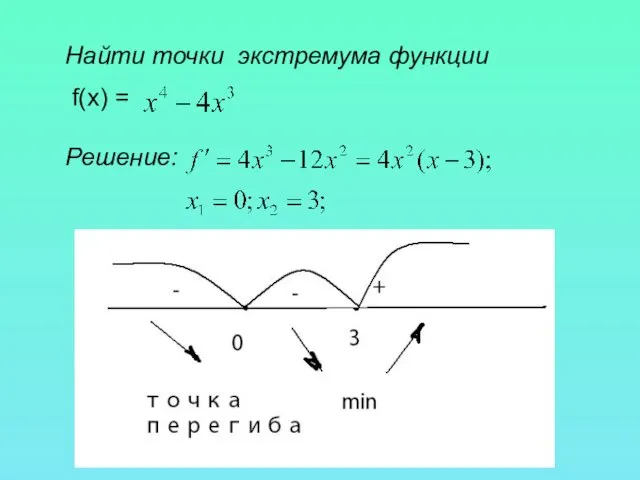
- 9. Найти точки экстремума функции f(x) = Решение:
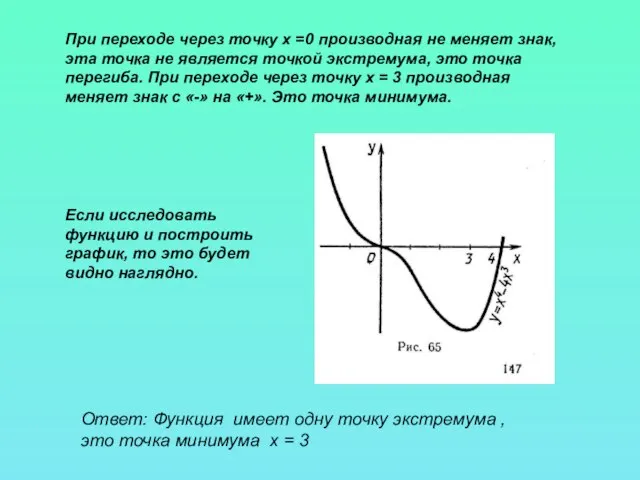
- 10. Ответ: Функция имеет одну точку экстремума , это точка минимума х = 3 При переходе через
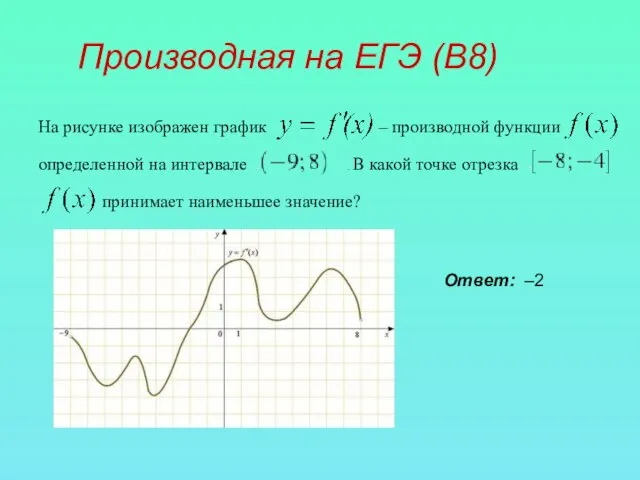
- 11. Производная на ЕГЭ (В8) На рисунке изображен график – производной функции определенной на интервале . В
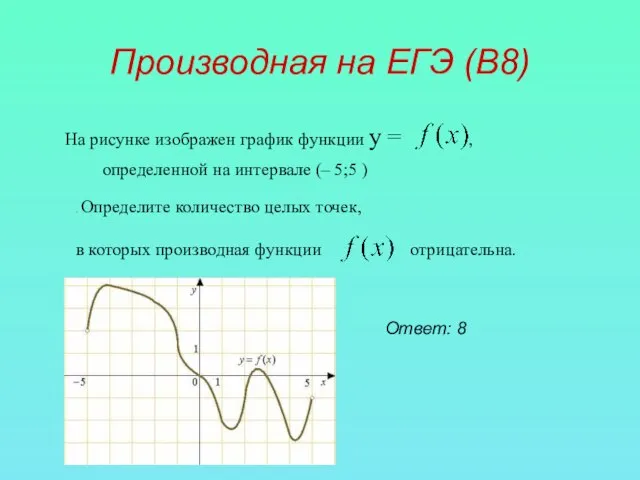
- 12. Производная на ЕГЭ (В8) На рисунке изображен график функции у = , определенной на интервале (–
- 13. Производная на ЕГЭ (В14) Найдите наименьшее значение функции у = х³ + 6х² +9х + 24
- 14. Использованные ресурсы: Открытый банк задач ЕГЭ по математике 2012 http://live.mephist.ru/show/mathege2010/ Обучающая система Д. Гущина «РЕШУ ЕГЭ»
- 16. Скачать презентацию








 УНИВЕРСИТЕТ ТОЛЕДО и НАРОДНАЯ УКРАИНСКАЯ АКАДЕМИЯ представляют совместную украино-американскую программу подготовки магистр
УНИВЕРСИТЕТ ТОЛЕДО и НАРОДНАЯ УКРАИНСКАЯ АКАДЕМИЯ представляют совместную украино-американскую программу подготовки магистр Время. События. Люди
Время. События. Люди Конструирование и моделирование юбки
Конструирование и моделирование юбки Презентация на тему Советские деньги
Презентация на тему Советские деньги  Правописание безударных личных окончаний глаголов I и I I спряжения
Правописание безударных личных окончаний глаголов I и I I спряжения Правовое регулирование реализации товаров, работ, услуг. Тема 6
Правовое регулирование реализации товаров, работ, услуг. Тема 6 История часов
История часов Готовимся к ГИА. Задание В4. Обособленные обстоятельства
Готовимся к ГИА. Задание В4. Обособленные обстоятельства Как справиться с негативными мыслями в голове
Как справиться с негативными мыслями в голове Преимущество для потребителя Комфорт Ваш дом никогда не замерзнет Обогрев и/или охлаждение жилища в ваше отсутствие Гостиная
Преимущество для потребителя Комфорт Ваш дом никогда не замерзнет Обогрев и/или охлаждение жилища в ваше отсутствие Гостиная Адаптационный период учащихся 1-х, 5-х, 10 классов. Особенности, итоги, выводы
Адаптационный период учащихся 1-х, 5-х, 10 классов. Особенности, итоги, выводы Молитва Иисуса
Молитва Иисуса Презентация на тему Происхождение и эволюция человека
Презентация на тему Происхождение и эволюция человека Термическая обработка стали
Термическая обработка стали Стилистико-речевые и логические ошибки
Стилистико-речевые и логические ошибки Bulk weighers
Bulk weighers Робототехника
Робототехника Обзор средств моделирования
Обзор средств моделирования Презентация на тему С огнем не играй - пожар не затевай!
Презентация на тему С огнем не играй - пожар не затевай! Создание продукта: от идеи к воплощению
Создание продукта: от идеи к воплощению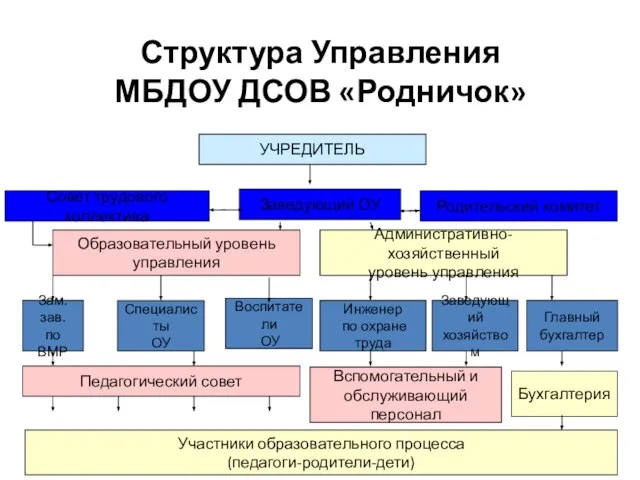 Структура Управления МБДОУ ДСОВ «Родничок»
Структура Управления МБДОУ ДСОВ «Родничок» Викторина «На сколько ты знаешь свой Казахстан?»
Викторина «На сколько ты знаешь свой Казахстан?» Шалость. Злонамеренный поступок. Вандализм
Шалость. Злонамеренный поступок. Вандализм От цифирной школы до цифровой
От цифирной школы до цифровой Шаблон презентации проекта
Шаблон презентации проекта Любимый город Набережные Челны
Любимый город Набережные Челны Ш ш
Ш ш Ты мастер декоративно прикладного искусства
Ты мастер декоративно прикладного искусства