Свойства ядерных сил. Модели ядер

При построении моделей ядра необходимо учитывать свойства сил, удерживающих протоны и нейтроны внутри ядра. Общей теории ядерных сил до сих пор не создано. Экспериментальные данные указывают на отдельные свойства ядерных сил. Часто свойства оказываются противоречивыми, чтобы создать одну модель, учитывающую все характеристики взаимодействия внутри ядра.
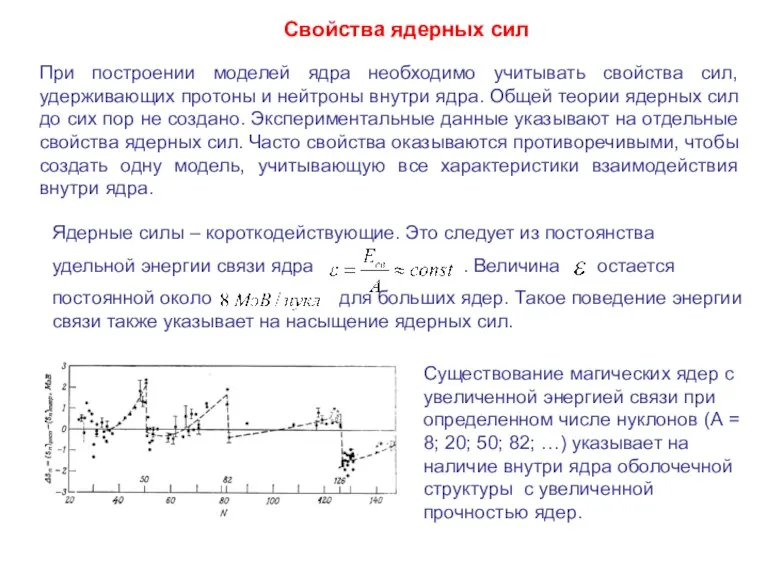
Свойства ядерных сил
Ядерные силы – короткодействующие. Это следует из постоянства
удельной энергии связи ядра . Величина остается
постоянной около для больших ядер. Такое поведение энергии связи также указывает на насыщение ядерных сил.
Существование магических ядер с увеличенной энергией связи при определенном числе нуклонов (А = 8; 20; 50; 82; …) указывает на наличие внутри ядра оболочечной структуры с увеличенной прочностью ядер.

Ядерные силы оказываются зарядово-независимыми. Экспериментально установлено, что парная энергия связи двух нуклонов за
счет взаимодействия остается практически одинаковой, за вычетом поправки на кулоновское отталкивание.
На это указывает одинаковая структура уровней зеркальных ядер (число протонов одного ядра равно числу нейтронов другого ядра, при
одинаковом массовом числе А: ).
Внутри ядра происходит парное спаривание нуклонов с компенсацией динамических характеристик, таких как спины, магнитные моменты. Для самых тяжелых ядер суммарные моменты (спины) не превышают
Свойства ядерных сил
Ядерные силы имеют сложный тензорный характер (не центральный).

Ядерные силы зависят от спин - орбитального взаимодействия нуклонов. Оказывается, что - при параллельном направлении спина и момента, энергия связи нуклона оказывается больше.
Ядерные силы носят локальный обменный характер. Переносчиком выступает виртуальный π-мезон с радиусом дальнодействия порядка 1 ферми (~1φ).
Существует симметрия между числом протонов и нейтронов.
Реально, с учетом кулоновского взаимодействия, уменьшающего внутреннюю энергию протонов, получается поднятие “дна” потенциала, что приводит к уменьшению числа протонов для стабильных ядер.
Плотность нуклонов внутри ядра остается практически постоянной – подобно состоянию капли вещества
Свойства ядерных сил

Общие характеристики моделей ядер
Модели ядер можно условно разделить на два класса: с сильной связью между частицами и независимым движением частиц внутри ядра.
К первому классу относится капельная модель, с короткодействующим сильным взаимодействием частиц на маленьких расстояниях r по сравнению с размером самого ядра (r << Rяд). Пробег взаимодействия (L) частиц внутри ядра, также предполагается маленьким (L<< Rяд). Состояние нуклона определяется только нуклонами его ближайшего окружения.
Эта модель объясняют энергетические характеристики ядра: возможность распада, деления, устойчивость ядер, энергию связи и др.
В модели независимых частиц предполагается, что отдельные нуклоны свободно движутся (по оболочкам) в усредненном потенциальном поле, образованном всеми частицами ядра. Пробег взаимодействия частиц получается большим (L>>Rяд). Большой пробег частиц для низкого состояния по энергии обусловлен принципом Паули для фермионов.
Эта модель объясняет динамические характеристики ядра - спин ядра, четность энергетических уровней, магнитный момент.

Капельная модель ядра
Короткодействующие силы и их насыщение указывает на адекватность представления ядер в виде капли, состоящей из отдельных фрагментов – нуклонов. На основе капельной модели построена полуэмпирическая формула для энергии связи ядра (формула Вайцзеккера):
ослабление энергии при неравенстве числа протонов и нейтронов
- учитывает изменения энергии связи для четно-нечетных ядер
- указывает на постоянство удельной энергии связи

Применение капельной модели ядра
Коэффициенты (МэВ): α = 15,75; β = 17,8; γ = 0,71; ξ = 94; η= 34 получены методом наилучшего согласия кривой удельной энергии связи ε(A,Z) для всего диапазона ядер A.
Из Есв(А,Z) можно получить связь между A и Z для максимальной
прочности ядер. Проведя дифференцирование
получаем
Отклонения ядер (A,Z) от Zуст приводит к β+ - или β- - распадам ядер, например
Можно рассчитать энергию Q и порог реакции
Массы ядер вычисляются по формуле

Капельная модель используется в теории ядерных реакций при невысоких энергиях, для объяснения характеристик долгоживущего промежуточного ядра О* и энергетического поведения сечений различных процессов для отдельных каналов распада ядра О*.
Модель также используется для оценки устойчивости ядер.
Модель хорошо объясняет энергетические характеристики реакций синтеза и деления ядер.
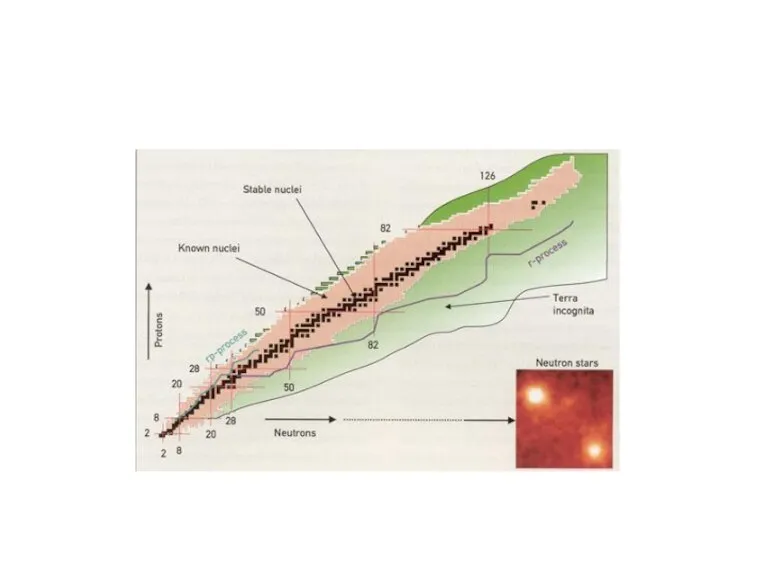
В соответствии с капельной моделью при A ≈ 300 энергия связи стремится к нулю, что ограничивает таблицу Менделеева по числу ядерно-устойчивых элементов в природе.
Применение капельной модели ядра