Тайны устного счёта

Цель моей работы – найти способы устных вычислений, для повышения вычислительной культуры и развития интереса к урокам математики.
Задачи:
Найти и изучить материал по данной теме «Тайны устного счёта»;
Выделить основные способы, которых легко можно использовать на уроках, сделать выводы, по использованию данных видов устных вычислений;
Чтобы навыки устных вычислений постоянно совершенствовались, необходимо установить правильное соотношение в применении устных и письменных приёмов вычислений, а именно: вычислять письменно только тогда, когда устно вычислять трудно.

Немного истории…

Система счёта.

Способы сложения.
Проще складывать числа по разрядам: отдельно сложив десятки и единицы, а потом сложив эти две суммы.
Примеры к первому способу поразрядного сложения:
28+84+67+31= (20+80+60+30)+(8+4+7+1)=190+20= 210
91+46+29+24= (90+40+20+20)+(1+6+9+4)=170+20=190

Способ вычитания.
Вычитание путём уравнивания числа единиц последних разрядов уменьшаемого.
67 - 48=(68 - 48) -1=20 - 1=19
453 - 316=(453 - 313) - 3=140 - 3=137
343 - 24= (344 - 24) - 1=320 - 1=319
648 - 329= (649 - 329) - 1=320 - 1=319

Умножение и деление
на 5, 50, 500 и т. д.
Например: 50 = 100 : 2 и т.д.
54 ⋅ 5 =(54 ⋅10) : 2 = 540 : 2 = 270
54 ⋅ 5 = (54 : 2) ⋅ 10 = 270
10800 : 50 = 10800 : 100 ⋅ 2 =216
10800 : 50 = 10800 ⋅ 2:100 =216

Умножение двузначных чисел, меньших, чем 20.
К одному из чисел надо прибавить количество единиц другого, эту сумму умножить на 10 и прибавить к ней произведение единиц данных чисел:
18 ⋅ 16 = (18 + 6) ⋅ 10 + 8 ⋅ 6 = 240 + 48 = 288.
Описанным способом можно умножать двузначные числа, меньшие 20, а также числа, в которых одинаковое количество десятков:
23 ⋅ 24 = (23 + 4) ⋅ 20 + 4 ⋅ 6 = 27 ⋅ 20 +12 = 540 + 12 = 562.

Умножение
двузначного числа на 101 .
Пожалуй, самое простое правило: припишите ваше число к самому себе. Умножение закончено.
Пример:
57 ⋅ 101 = 5757 57 → 5757

Умножение числа на 11
Следует "раздвинуть" цифры числа, умножаемого на 11, и в образовавшийся промежуток вписать сумму этих цифр, причем если эта сумма больше 9, то, как при обычном сложении, следует единицу перенести в старший разряд.
Пример:
34 ⋅ 11 = 374, так как 3 + 4 = 7, семерку помещаем между тройкой и четверкой
68 ⋅ 11 = 748, так как 6 + 8 = 14, четверку помещаем между семеркой (шестерка плюс перенесенная единица) и восьмеркой

Умножение
на 22, 33, 44, 55, 66, 77, 88, 99.
Чтобы двузначное число умножить 22,33, …,99, надо этот множитель представить в виде произведения однозначного числа на 11. Выполнить умножение сначала на однозначное число, а потом на 11:
15 ⋅ 33 = 15 ⋅ 3 ⋅ 11= 45 ⋅ 11 = 495
23 ⋅ 66 = 23 ⋅ 6 ⋅ 11= 138 ⋅ 11= 1518

Умножение на 37.
При умножении числа на 37, если данное число кратно 3, его делят на 3 и умножают на 111.
27 ⋅ 37=(27 : 3) ⋅ (37 ⋅ 3) = 9 ⋅ 111= 999
Если же данное число не кратно 3, то из произведения вычитают 37 или к произведению прибавляют 37.
23 ⋅ 37 = (24 - 1) ⋅ 37 = (24 : 3) ⋅ (37 ⋅ 3) – 37 = 888 – 37 = 851.

Возведение в квадрат числа, оканчивающееся на 5.
Число десятков умножаем на следующее число десятков и прибавляем 25.
15 ⋅ 15 = 225 = 10 ⋅ 20 + 25
(или 1 ⋅ 2 и приписываем справа 25)
35 ⋅ 35 =30 ⋅ 40 +25 = 1225
(3 ⋅ 4 и приписываем справа 25)
65 ⋅ 65 = 60 ⋅ 70+25 = 4225
(6 ⋅ 7 и приписываем справа 25)

Таблица умножения на 9

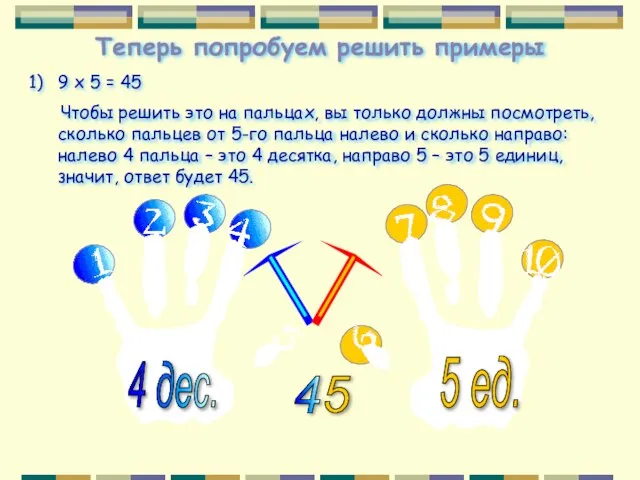
Теперь попробуем решить примеры
9 х 5 = 45
Чтобы решить это на пальцах, вы только должны посмотреть, сколько пальцев от 5-го пальца налево и сколько направо: налево 4 пальца – это 4 десятка, направо 5 – это 5 единиц, значит, ответ будет 45.
4 дес.
5 ед.
4
5

Секреты таблицы
умножения числа 5.
5 *2 = 10
5 * 3 = 15
5 *4 = 20
5 * 5 = 25
5* 6 = 30
5 * 7 = 35
5* 8 = 40
5 * 9 = 45
Мои наблюдения:
1. Произведения заканчиваются цифрами 5 или 0.
2. Если второй множитель четный, то произведения заканчиваются на 0.
3. Если второй множитель нечетный, то произведения заканчиваются цифрой 5.
4. А цифра в разряде десятков может быть получена представлением второго множителя в виде суммы одинаковых чисел, одно из которых берем в десяток, если есть остаток, его надо отбросить.

Заключение:
В результате проделанной работы я выполнила следующие задачи:
Изучила литературу по данному вопросу.
Научилась использовать описанные способы.
Выступила перед своими одноклассниками и ознакомила их с приемами быстрого умножения.
В перспективе на будушее
я планирую продолжить
работу с числами,
так как в нашей жизни,
числа играю важную роль.