Телеконференция. Энциклопедия

ЭНЦИКЛОПЕДИЯ
(от греч. enkyklios paideia - обучение по всему кругу знаний) – научное или научно-популярное справочное издание, содержащее систематизированный свод знаний.

Телевидение - Передача на расстоянии и прием на экран средствами радиоэлектроники изображений движущихся и неподвижных объектов и звукового сопровождения
Конференция - (ср.-век. лат. conferentia - от лат. confero - собираю в одно место),

Телеконференция
-обмен информацией по определенной тематике между пользователями

Журнал
- (франц. journal - первоначально - дневник), печатное периодическое издание.
Первым журналом считается ""Журналь де саван"" ( Франция, 1665).
В России первый журнал - приложение к газете""Санкт-Петербургские ведомости"" - ""Месячные исторические, генеалогические и географические примечания в Ведомостях"" (1728).

Чтение- вот лучшее учение!
Знания имей отличные по теме
«Дроби десятичные»

Какие действия с десятичными дробями вы умеете выполнять?
Какие законы и правила действуют на множестве десятичных дробей?

Сравнение
округление
сложение
вычитание
умножение
деление

30,07
5,645
108,2
17,289
5,7
108,200
2.
0,789
0,7801
0,78
>
<

До сотых: 3,625
До сотен: 6329,85
До десятых: 87,52
3,63
‹
6300
87,5
4 ,62 ≈ 5 6,8 3 5 ≈ 6,8
4, 2 3 5 ≈ 4,24

6,3 6 83,2
1 2,3 1,9
+
+
7,5 9
8,5 1
6,36 + 12,3
83,2 + 1,9
75,6 + 136,92
18,66
85,1
212,52
№1

1,2
3,9
12,2 - 9,6
7,3 – 4,568
5 – 0,61
2,6
2,732
4,39
№2

Когда и где появились десятичные дроби?

Из истории
Человечество пользуется дробными числами уже несколько тысячелетий , а вот записывать их удобными десятичными знаками оно додумалось значительно позже.

В древнем Китае дробь вида 2,135436
выглядела так:
2 чи, 1 цунь, 3 доли, 5
порядковых,
4 шерстинки, 3 тончайших, 6 паутинок.

Арабский математик
Аль-Каши Джемшид Ибн Масуд,
работавший в городе Самарканде в обсерватории Улугбека в начале 15 века, записывал дроби так
2135436
или
2|135436

В своей книге "Десятая" он не только излагает теорию десятичных дробей, но и старается убедить людей пользоваться ими, говоря, что при их использовании "изживаются трудности, распри, ошибки, потери и прочие случайности, обычные спутники расчетов". Его и считают изобретателем десятичных дробей.
Лишь в конце XVI века мысль записывать дробные числа десятичными знаками пришла некоему Симону Стевину
из Фландрии. В своей книге "Десятая" (1585г.)
он предлагает писать цифры дробного числа
в одну строку с цифрами целого числа, при этом нумеруя их. Например, число записывалось так:
0,3752 = или 5,13=

Примерно в это же время математики Европы также пытались найти удобную запись десятичной дроби.
В книге "Математический канон"
французского математика
Ф. Виета (1540-1603)
десятичная дробь записана так
2 135436 - дробная часть подчеркивалась и записывалась выше строки целой части числа.

1617 г. - шотландский математик Джон Непер
предложил отделять десятичные знаки
от целого числа либо запятой, либо точкой.
1592 г. - в записи дробей впервые встречается запятая.
1571 г. – Иоган Кеплер предложил современную запись десятичных дробей, т.е. отделение целой части запятой. До него существовали другие варианты: 3,7 писали как 3(0)7 или 3\ 7 или разными чернилами целую и дробную части.
1703 год - В России учение о десятичных дробях изложил Л.Ф.Магницкий в, в учебнике
«Арифметика , сиречь наука числительная».
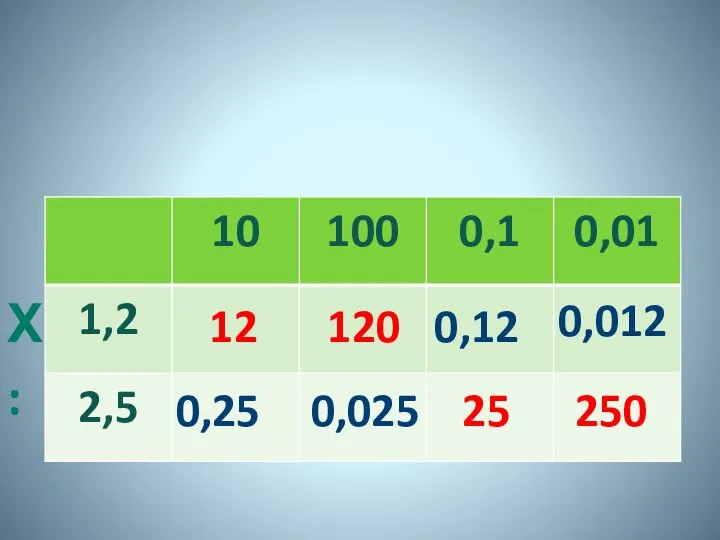
В странах, где говорят по-английски (Англия, США, Канада и др.), и сейчас вместо запятой пишут точку, например: 2.3

12
120
0,12
0,012
0,25
0,025
25
250
Х
:

32, 5*0,51=? Почему результат после умножения уменьшается?
36, 5: 0, 8=? Почему результат после умножения увеличивается?

6,3 : 3
18,06 : 6
1,6 : 8
м
а
й
25,032 : 0,56
13,201 : 4,3
44,7
3,07
№3

Вычислить удобным способом
14,95 *11 + 15,05 * 11
31,491 * 627 – 30,491 *627
4 * 0,25*0,6
1,5*0,6*0,5*4
( 6,4 *27 + 6,4 * 23) : 5