Слайд 2ЗАДАЧА 1
Два мебельных мастера, работая вместе, могут за 1 неделю собрать 50

столов. Работая отдельно, первый мастер собирает 60 столов на одну неделю дольше, чем такое же число столов собирает второй мастер. За
сколько недель первый мастер соберет 40 столов?
Слайд 3Решение
Пусть первый мастер собирает за неделю x столов, тогда второй- 50-х столов.

Тогда 60 столов первый мастер соберет за 60:х недель, а второй за 60:(50-х) недель. Зная, что первый мастер собирает 60 столов на 1 неделю дольше, составим и решим уравнение:
Решая его, находим корни х=20; х=150.
х=150 не удовлетворяет условию задачи, значит для нашей задачи х=20.
Значит 40 столов он соберет за 40:20=2(недели).
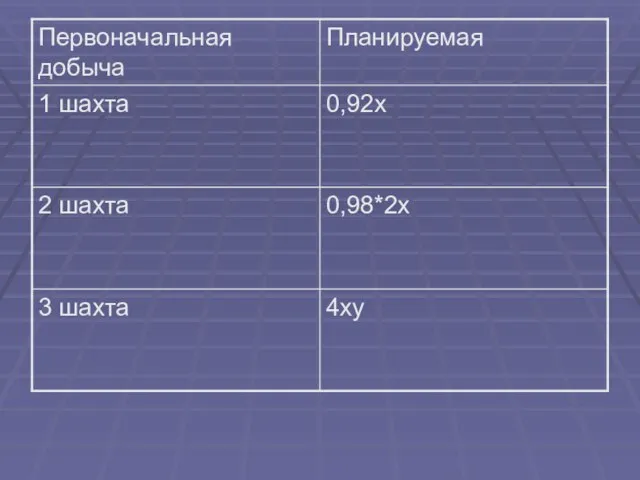
Слайд 4Задача 2
Объемы ежегодной добычи угля первой, второй и третьей шахтами
относятся как

1: 2: 4. Первая шахта планирует уменьшить годовую
добычу угля на 8%, а вторая – на 2%. На сколько процентов должна
увеличить годовую добычу угля третья шахта, чтобы суммарный объем
добываемого за год угля не изменился?
Слайд 6Зная, что суммарный объем добываемого угля не должен измениться, составим и решим

уравнение:
Слайд 7Зная, что х не равен нулю, т.к. величина 1 части не может

быть нулевой, разделим данное уравнение на х.
Вывод: добыча угля 3 шахтой должна увеличится на 3 %.
Слайд 8Задача 3
В первый день подготовки к экзамену школьник повторил 3 вопроса. В

каждый следующий день он повторял на 2 вопроса больше, чем в предыдущий, и успел вовремя подготовить все 48 вопросов программы. Сколько дней заняла подготовка?
Слайд 9Имеется арифметическая прогрессия
a1=3, d=2. Пусть n(натуральное число) - число дней, потраченных на

подготовку.
Тогда количество повторенных вопросов(48 вопросов) равно сумме n членов этой арифметической прогрессии
Решая, получаем :
n=6







 Методическое объединение учителей математики и информатики
Методическое объединение учителей математики и информатики Аналитическая роспись официальных документов в базах данных Президентской библиотеки Республики Беларусь
Аналитическая роспись официальных документов в базах данных Президентской библиотеки Республики Беларусь Методика изучения фонетики и графики в начальной школе
Методика изучения фонетики и графики в начальной школе 14-18 февраля 2012г в Москве проходил важный форум психологов России-5 съезд Российского Психологического общества (РПО) -см. рпо.рф, Т
14-18 февраля 2012г в Москве проходил важный форум психологов России-5 съезд Российского Психологического общества (РПО) -см. рпо.рф, Т Детали машин и основы конструирования. Разъемные и неразъемные соединения
Детали машин и основы конструирования. Разъемные и неразъемные соединения Значение антимонопольного регулирования в формировании конкурентных отношений в российской электроэнергетике
Значение антимонопольного регулирования в формировании конкурентных отношений в российской электроэнергетике kantemir (2)
kantemir (2) История развития горнозаводского производства на Урале в XIX в
История развития горнозаводского производства на Урале в XIX в 20141003_urok_1_chast
20141003_urok_1_chast Международный день чая
Международный день чая Реформы Н.С. Хрущева
Реформы Н.С. Хрущева Безопасность в интернете
Безопасность в интернете Тесты по технологии. 6 класс
Тесты по технологии. 6 класс Герои и темы народного эпоса
Герои и темы народного эпоса Презентация на тему Давление жидкости
Презентация на тему Давление жидкости Индивидуальное логопедическое занятие
Индивидуальное логопедическое занятие «Бизнес.Эффективность.Развитие.Системность.»
«Бизнес.Эффективность.Развитие.Системность.» Дворец Moxó 1770 года постройки, является архитектурным наследием Барселоны. Дворец был построен под руководством Francisco Mestres в стиле б
Дворец Moxó 1770 года постройки, является архитектурным наследием Барселоны. Дворец был построен под руководством Francisco Mestres в стиле б Objectives
Objectives СИСТЕМА ДИСТАНЦИОННОЙ ПОДГОТОВКИ к сдаче экзаменов в форме ЕГЭ и ГИА «СТАТГРАД»
СИСТЕМА ДИСТАНЦИОННОЙ ПОДГОТОВКИ к сдаче экзаменов в форме ЕГЭ и ГИА «СТАТГРАД» Ангиография
Ангиография Клуб «Любителей природы»
Клуб «Любителей природы» Media People
Media People Маркетинг Lady Stretch
Маркетинг Lady Stretch Сочинение по картине П. П. Кончаловского "Сирень в корзине"
Сочинение по картине П. П. Кончаловского "Сирень в корзине" Работы французский узелок и шов рококо (7 класс)
Работы французский узелок и шов рококо (7 класс) Строение и функции кожи. Гигиена кожи
Строение и функции кожи. Гигиена кожи Создание семьи
Создание семьи