Содержание
- 2. Цели урока: Ознакомить учащихся с понятиями смежных и вертикальных углов, рассмотреть их свойства; Научить строить угол,
- 3. Давай вспомним! Что такое угол?
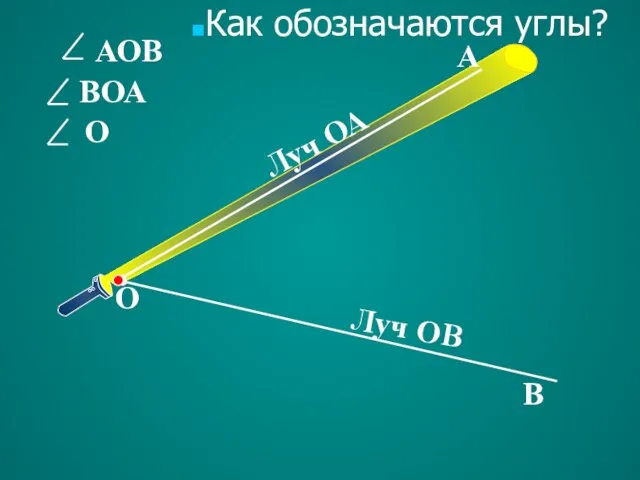
- 4. АОВ О В ВОА А О Луч ОА Луч ОВ Как обозначаются углы?
- 5. Для измерения углов используют транспортир . Какой инструмент можно использовать для измерения углов?
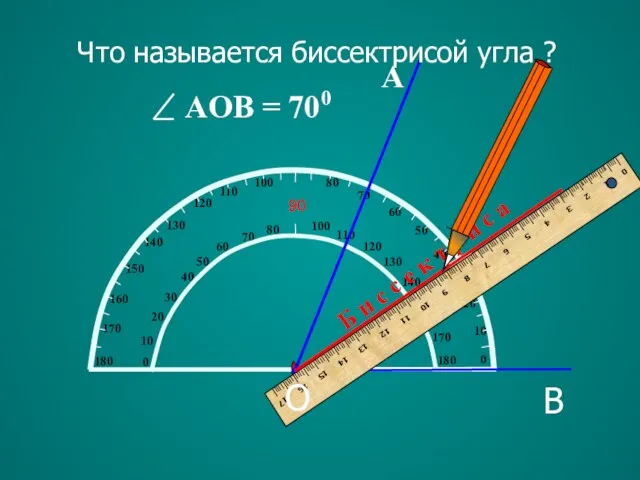
- 6. А Б и с с е к т р и с а Что называется биссектрисой угла
- 7. Единицы измерения угла Всего 180 частей. 1 часть – это 1 градус. 1/60 часть градуса называется
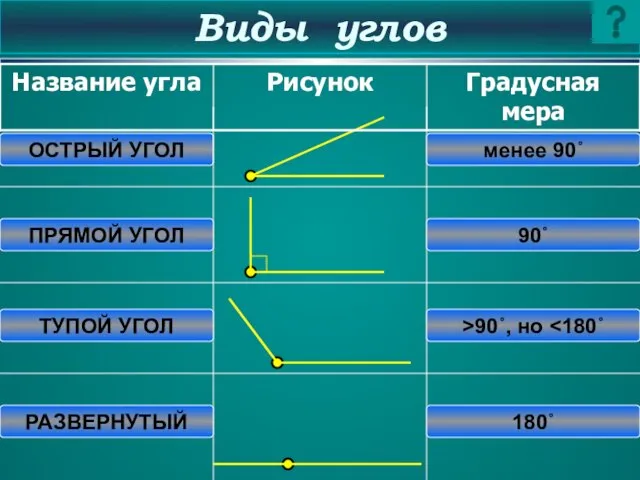
- 8. Виды углов ОСТРЫЙ УГОЛ ПРЯМОЙ УГОЛ ТУПОЙ УГОЛ РАЗВЕРНУТЫЙ менее 90˚ 90˚ >90˚, но 180˚
- 9. Какой угол образует клюв вороны, когда: "Ворона сыр во рту держала?" А когда "Ворона каркнула во
- 10. Острый Тупой
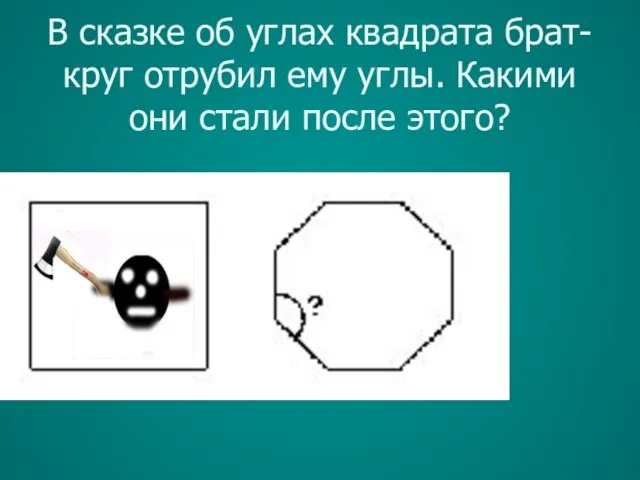
- 11. В сказке об углах квадрата брат-круг отрубил ему углы. Какими они стали после этого?
- 12. К вашим знаниям об углах сегодня добавится еще два вида: Смежные и вертикальные углы.
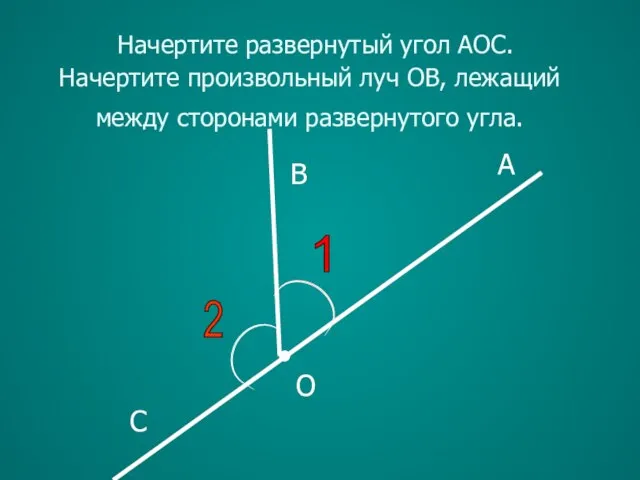
- 13. 1 A B C O Начертите развернутый угол АОС. Начертите произвольный луч ОB, лежащий между сторонами
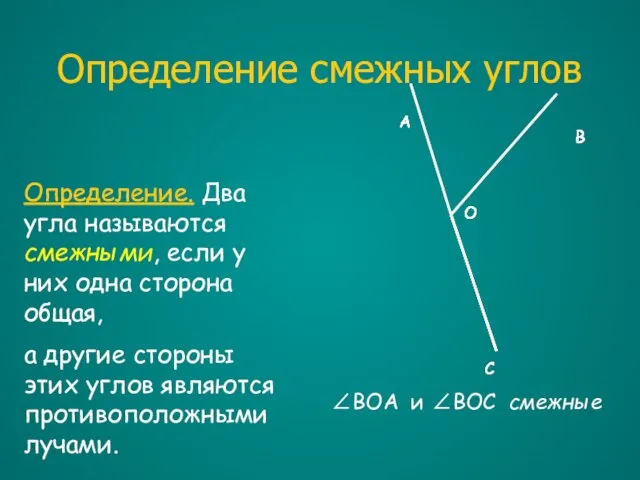
- 14. Определение смежных углов Определение. Два угла называются смежными, если у них одна сторона общая, а другие
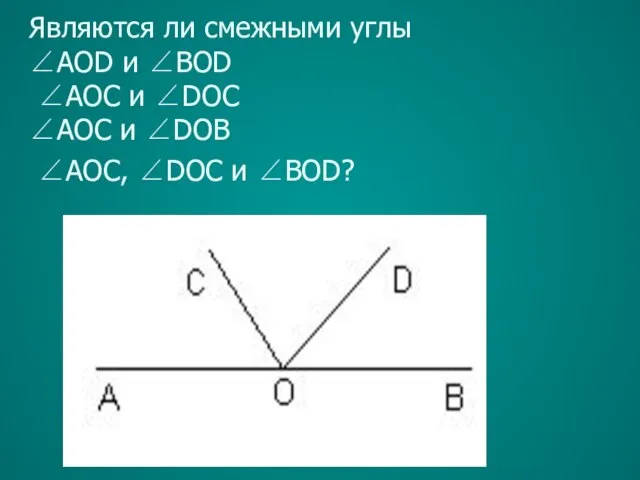
- 15. Являются ли смежными углы ∠AOD и ∠BOD ∠AOС и ∠DOС ∠AOС и ∠DOВ ∠AOС, ∠DOС и
- 16. Построение смежных углов
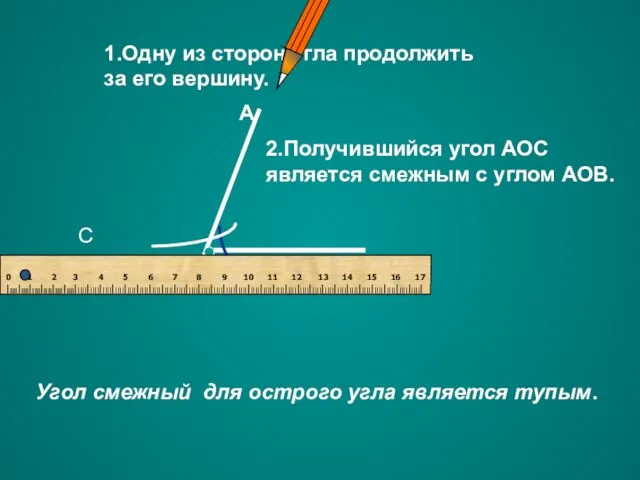
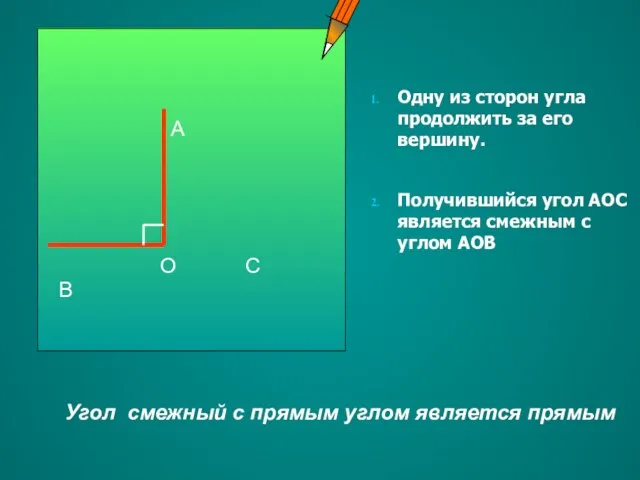
- 17. А О В С Угол смежный для острого угла является тупым. 1.Одну из сторон угла продолжить
- 18. 1. Одну из сторон угла продолжить за его вершину. 2. Получившийся угол АОС является смежным для
- 19. Одну из сторон угла продолжить за его вершину. Получившийся угол АОС является смежным с углом АОВ
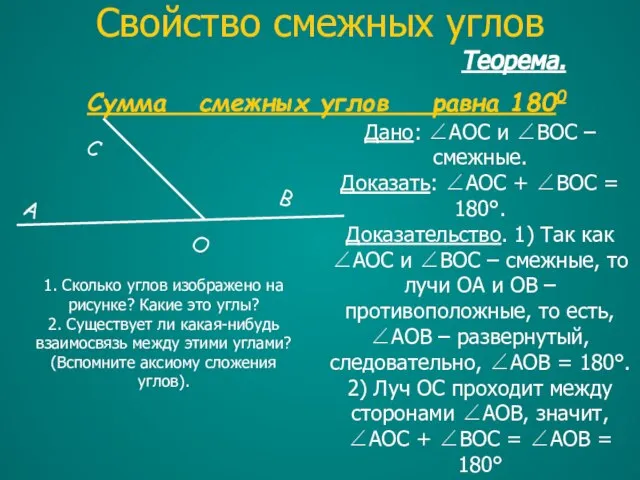
- 20. Теорема. Сумма смежных углов равна 1800 Дано: ∠AOC и ∠BOC – смежные. Доказать: ∠AOC + ∠BOC
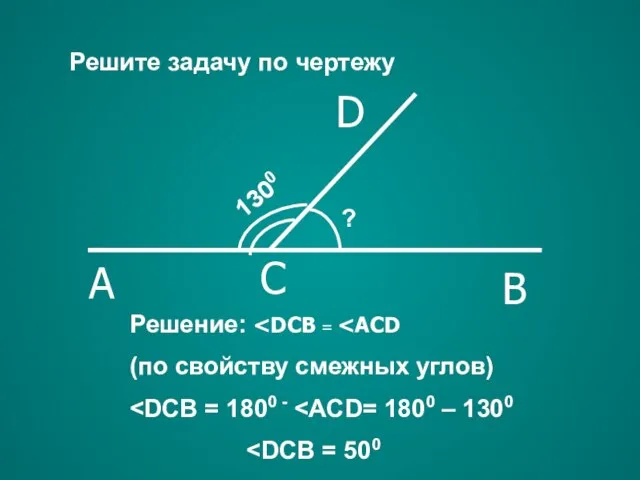
- 21. Решение: (по свойству смежных углов) Решите задачу по чертежу A C B D
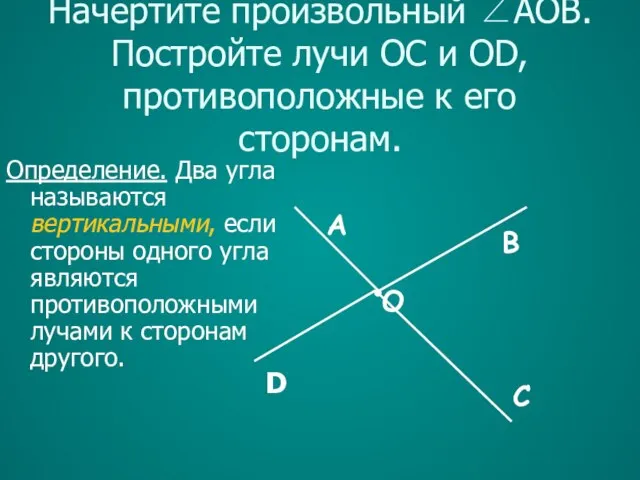
- 22. Начертите произвольный ∠AOB. Постройте лучи OC и OD, противоположные к его сторонам. В С D Определение.
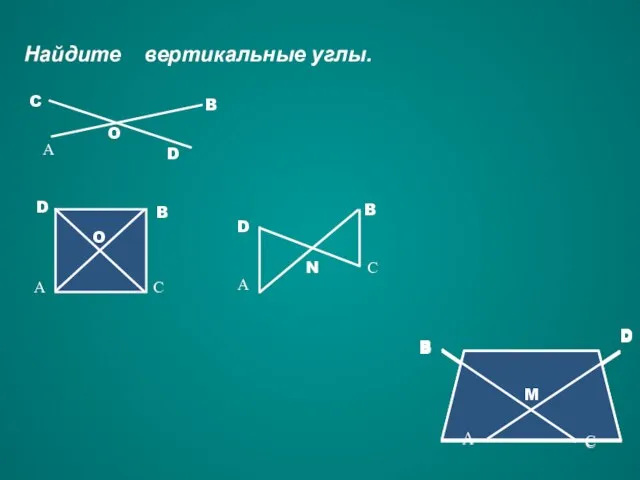
- 23. Найдите вертикальные углы. M N D С B А M D С B А
- 24. Построение вертикальных углов
- 25. C D Построить угол. 2.Продлить каждую сторону угла за его вершину. А
- 26. Свойство вертикальных углов Теорема. Вертикальные углы равны. Дано: ∠AOD и ∠COB – вертикальные. Доказать: ∠AOD=∠COB Доказательство.
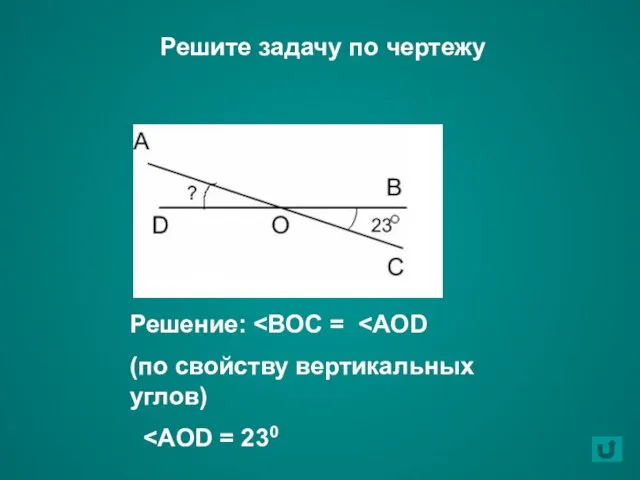
- 27. Решите задачу по чертежу Решение: (по свойству вертикальных углов)
- 28. Закончи предложение Если один из смежных углов равен 50°, то другой равен… Угол, смежный с прямым,
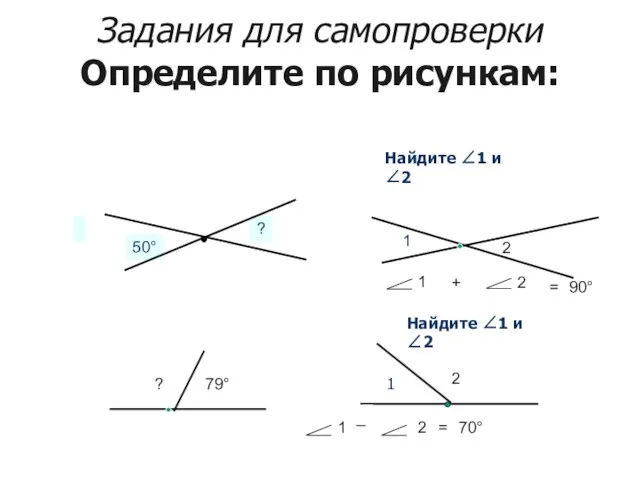
- 29. Задания для самопроверки Определите по рисункам: Найдите ∠1 и ∠2 1 Найдите ∠1 и ∠2
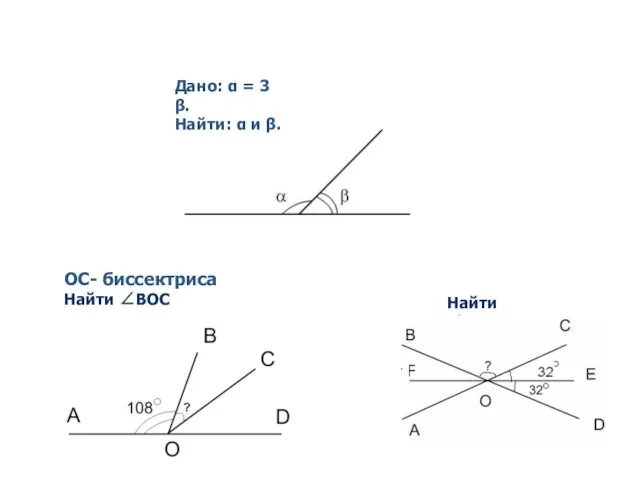
- 30. Дано: α = 3 β. Найти: α и β. ОС- биссектриса Найти ∠BOC Найти ∠BOC
- 31. Т Е С Т по теме "Вертикальные и смежные углы"
- 32. 1. Сумма смежных углов равна…. 3600 900 1800 A B C
- 33. 2. Как называется угол меньше 1800, но больше 900 острый тупой прямой A B C
- 34. 3. Чему равен угол, если смежный с ним равен 470? 1330 470 430 C B A
- 35. 4. Какой угол образуют часовая и минутная стрелки часов, когда они показывают 6 часов? тупой развернутый
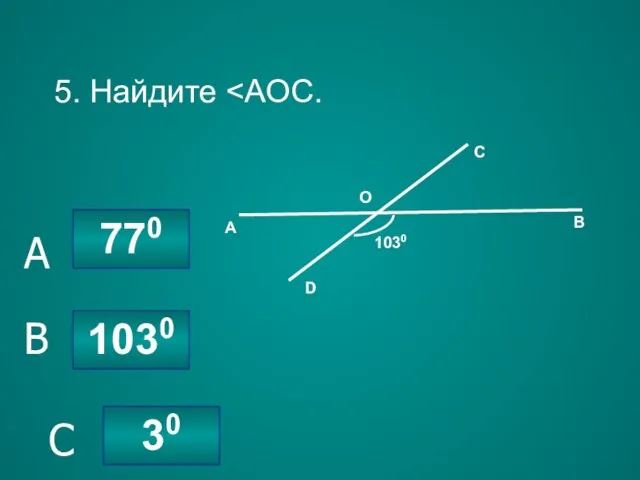
- 36. 5. Найдите 1030 770 30 C B A
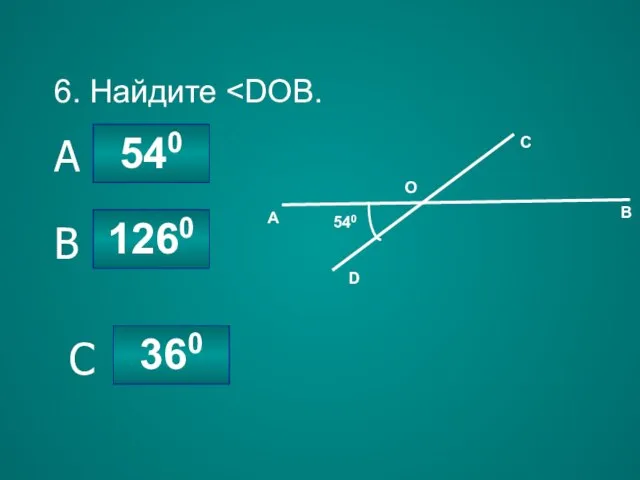
- 37. 6. Найдите 360 1260 540 B A C
- 38. 7. Найдите смежные углы, если один из них в два раза больше другого. 600 и 1200
- 39. 8. Угол равен 720. Чему равен вертикальный ему угол? 720 1080 180 C B A
- 40. 9. Какой угол образуют часовая и минутная стрелки часов, когда они показывают три часа? острый тупой
- 41. Проверь себя. 1. C 2. B 3. A 4. B 5. B 6. B 7. B
- 42. Образец оформления решения задачи При пересечении двух прямых образовалось четыре угла. Один из них равен 430.
- 43. Задача 1. Найдите углы, полученные при пересечении двух прямых, если один из углов равен 102 0.
- 45. Скачать презентацию
























 Время и календарь
Время и календарь Методические рекомендации по организации портфолио по курсу «Юридическая психология»
Методические рекомендации по организации портфолио по курсу «Юридическая психология» Яркие представители мира динозавров
Яркие представители мира динозавров Тип кольчатые черви 7 класс
Тип кольчатые черви 7 класс Дизайн и реклама – составляющие художественной культуры
Дизайн и реклама – составляющие художественной культуры Рождение капитализма (новый общественный строй)
Рождение капитализма (новый общественный строй) Сущность и принципы маркетинга
Сущность и принципы маркетинга Древние мифы, легенды, сказки, предания, благожеланиея дальневосточной земли.
Древние мифы, легенды, сказки, предания, благожеланиея дальневосточной земли. Всероссийский День правовой помощи детям. Права человека
Всероссийский День правовой помощи детям. Права человека Талант помогает исправиться
Талант помогает исправиться Зинин
Зинин Urok_11
Urok_11 Политическое поведение
Политическое поведение Спорт в Британии
Спорт в Британии Таможенное оформление круизных лайнеров и их пассажиров
Таможенное оформление круизных лайнеров и их пассажиров «Построение маркетинговых коммуникаций с молодёжной аудиторией в соответствии с её образом жизни и моделью потребления»
«Построение маркетинговых коммуникаций с молодёжной аудиторией в соответствии с её образом жизни и моделью потребления» Виды Дверей
Виды Дверей Рецепция римского права
Рецепция римского права 幅作品. 戴花的惠安阿婆
幅作品. 戴花的惠安阿婆 Основы научных исследований и инновационной деятельности
Основы научных исследований и инновационной деятельности “Fried Green Tomatoes at the Whistle Stop Café”
“Fried Green Tomatoes at the Whistle Stop Café” Синяя лента апреля
Синяя лента апреля Формы и системы оплаты труда на предприятиях
Формы и системы оплаты труда на предприятиях КАК ОРГАНИЗОВАТЬ КОНКУРС КИО В ШКОЛЕ
КАК ОРГАНИЗОВАТЬ КОНКУРС КИО В ШКОЛЕ Числа с собственными именами
Числа с собственными именами Послеоперационный период
Послеоперационный период  Программа amoCRM
Программа amoCRM Реализация PR и IR стратегий: особенности национального информационного поля
Реализация PR и IR стратегий: особенности национального информационного поля