Содержание
- 2. Французский юрист и математик 1601-1665 ПЬЕР ФЕРМА
- 3. Немецкий физик и математик 1777-1855 К. Ф. ГАУСС
- 4. Великий русский математик (1792-1856) Н.И. ЛОБАЧЕВСКИЙ
- 5. скалярные длина масса температура плотность и т.д. векторные перемещение скорость сила ускорение и т.д. Т и
- 6. Векторная величина определяется числовым значением и направлением Геометрической абстракцией векторной величины есть вектор – направленный отрезок
- 7. Действия с векторами Сложение векторов Определение: Суммой векторов называется вектор, замыкающий ломаную, построенную из данных векторов
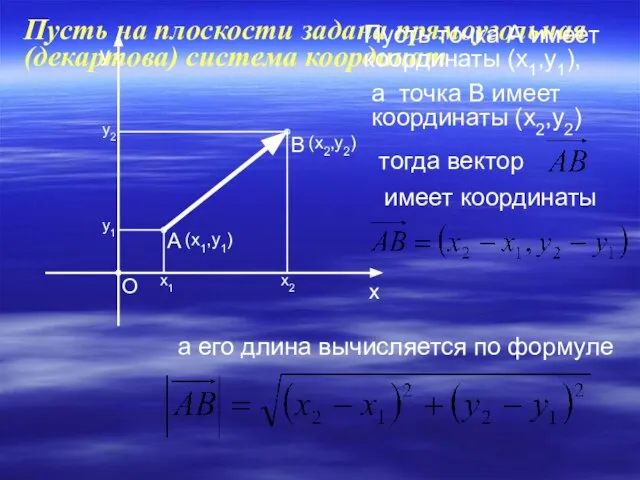
- 8. Пусть на плоскости задана прямоугольная (декартова) система координат Пусть точка А имеет координаты (х1,у1), х1 х2
- 9. Скалярное произведение векторов Из скалярного произведения находят угол между векторами Если вектора заданы своими координатами тогда
- 10. Работа А силы , произведенная этой силой при перемещении тела на пути , определяемом вектором ,
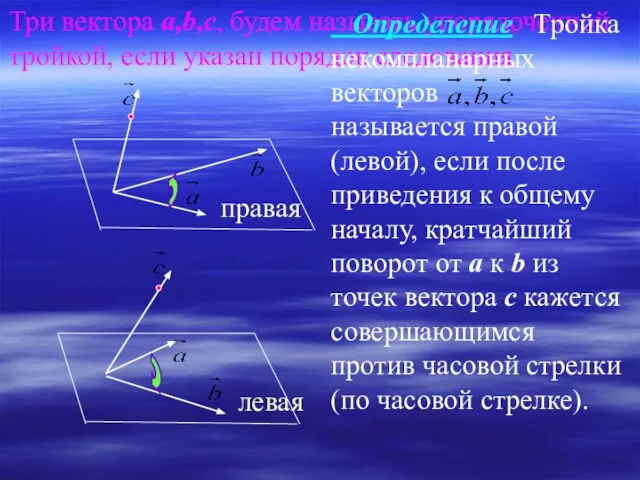
- 11. Три вектора а,b,c, будем называть упорядоченной тройкой, если указан порядок следования правая левая
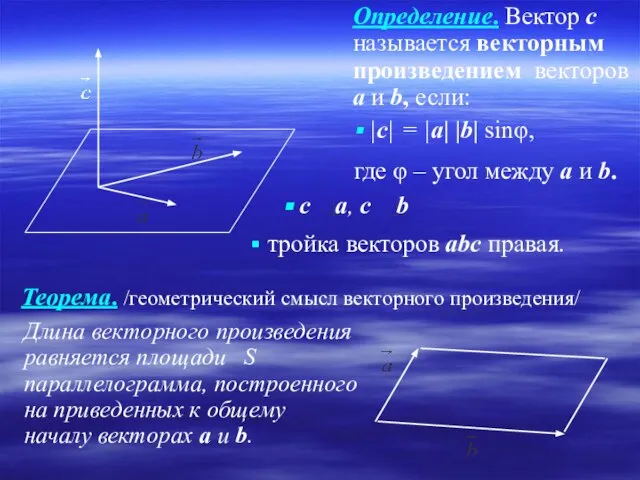
- 12. Определение. Вектор c называется векторным произведением векторов а и b, если: |c| = |a| |b| sinφ,
- 13. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ В КООРДИНАТНОЙ ФОРМЕ Пусть вектора заданы своими координатами тогда координаты векторного произведения вычисляются по
- 14. С помощью векторного произведения можно вычислить вращающий момент М силы F, приложенной к точке В тела,
- 15. Смешанное произведение векторов Определение Пусть даны три вектора a, b, c. Если вектор a векторно умножить
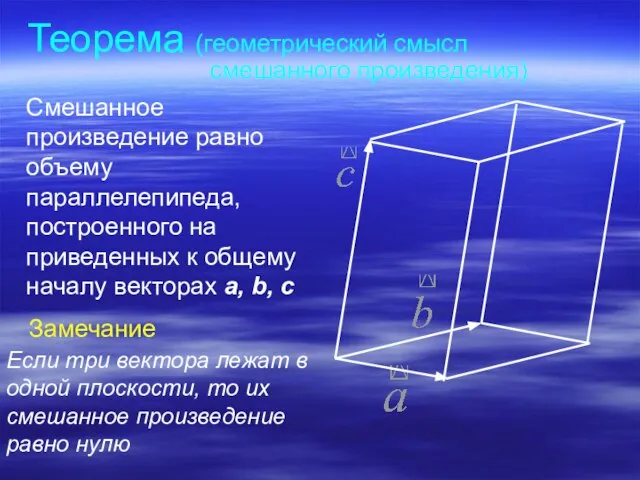
- 16. Теорема (геометрический смысл смешанного произведения) Смешанное произведение равно объему параллелепипеда, построенного на приведенных к общему началу
- 17. СМЕШАННОЕ ПРОИЗВЕДЕНИЕ В КООРДИНАТНОЙ ФОРМЕ Если три вектора определены своими декартовыми координатами то смешанное произведение равняется
- 18. ЗАДАЧА № 1 Даны координаты вершин пирамиды Методами векторной алгебры определить Угол между ребрами А1А2 и
- 20. Скачать презентацию













 Материальное стимулирование труда
Материальное стимулирование труда Овердрафт
Овердрафт Государственный бюджет США
Государственный бюджет США Критические компоненты и параметры ПЦР
Критические компоненты и параметры ПЦР Управление человеческими ресурсами. Реинжиниринг персонала. (Тема 10)
Управление человеческими ресурсами. Реинжиниринг персонала. (Тема 10) Сочинение по картине
Сочинение по картине Эпоха просвещения
Эпоха просвещения Иитерактивная доска
Иитерактивная доска Образ Москвы в русской литературе XIX века
Образ Москвы в русской литературе XIX века Неотложные состояния у больных с заболеванием органов дыхания
Неотложные состояния у больных с заболеванием органов дыхания  Педагогический конфликт
Педагогический конфликт Профессия моей мечты - учитель
Профессия моей мечты - учитель Все народы воспевают материнство
Все народы воспевают материнство Презентация на тему Письменность и знания древних египтян
Презентация на тему Письменность и знания древних египтян  Пассажирские и товарные вагоны
Пассажирские и товарные вагоны Применение металлов и их сплавов
Применение металлов и их сплавов Презентация урока «Многообразие птиц»
Презентация урока «Многообразие птиц» Интересные и быстрые способы и приемы вычислений
Интересные и быстрые способы и приемы вычислений Стресс. Виды стресса
Стресс. Виды стресса Информационное превосходство
Информационное превосходство 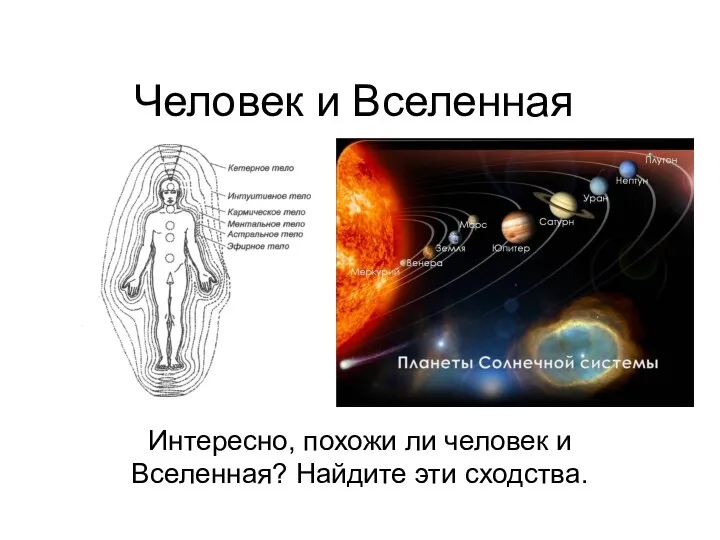 Человек и Вселенная
Человек и Вселенная «Предпрофильная подготовка и профильное обучение как форма социокультурного развития школьника»
«Предпрофильная подготовка и профильное обучение как форма социокультурного развития школьника» Презентация на тему Англия в эпоху Тюдоров
Презентация на тему Англия в эпоху Тюдоров  С Новым годом, ребятня - презентация для начальной школы_
С Новым годом, ребятня - презентация для начальной школы_ Детство - это смех и радость
Детство - это смех и радость Популяризация культурного наследия калмыков средствами массовой культуры
Популяризация культурного наследия калмыков средствами массовой культуры АЙСБЕРГ
АЙСБЕРГ Фонд Дмитрия Зимина «ДИНАСТИЯ»
Фонд Дмитрия Зимина «ДИНАСТИЯ»