Слайд 2 Цель и задача урока
Цель данного урока знакомство с жизнедеятельностью философа и

мыслителя Фалеса и его теоремой; развитие «геометрического зрения», расширение кругозора в плане знакомства с историей развития математики.
Задачи:
- продемонстрировать возможности применения теоремы Фалеса в различных геометрических задачах
- расширить представления о сферах применения полученных математических знаний;
- познакомиться с историческими сведениями об ученом Фалесе, о развитии математических знаний и их применениях
Слайд 3 Фалес
Фалес из Милета - первый древнегреческий мыслитель. По-видимому, он жил

в 640-546 годах до н.э. Он первый применил доказательство теорем и ввел их в обиход математики. Основатель милетской школы. Считался первым из Семи мудрецов Греции.
Слайд 4 Фалес считается родоначальником античной и, как следствие, европейской философии и науки.

Считался первым из Семи мудрецов Греции.
Важнейшей заслугой Фалеса в области математики должно быть перенесенное им из Египта в Грецию первых начал теоретической элементарной геометрии. Эвдем, по свидетельству Прокла, приписывает Фалесу открытие следующих геометрических предложений:
▪ Вертикальные углы равны.
▪ Углы при основании равнобедренного треугольника равны.
▪ Треугольник определяется стороной и прилежащими к ней двумя углами.
▪ Диаметр делит круг на две равные части.
Слайд 5Теорема Фалеса
Если параллельные прямые, пересекающие стороны угла, отсекают на одной его

стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне
Слайд 6Доказательство:
Пусть А3ОВ3 – заданный угол, а А1В1, А2В2, и А3В3– попарно

параллельные прямые и А1А2=А2А3. Докажем, что В1В2=В2В3. Проведем через точку В2 прямую С1С2 параллельную прямой А1А3. По лемме А1А2 =С1В2, А2А3 = В2С2 и с учетом условия теоремы С1В2 = В2С2. Кроме того, ∠В1С1В2 = ∠В2С2В33– как внутренние накрест лежащие при параллельных прямых А1В1, А3В3 и секущей С1С2 , а ∠В1В2С1 = ∠С2В2В3 как вертикальные. По второму признаку равенства треугольников ΔВ1С1В2 = ΔВ3С2В2. Отсюда В1В2 = В2В3. Теорема доказана.
Слайд 7 Теорема Фалеса
Если на одной из двух прямых отложить последовательно несколько

равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
Слайд 8Доказательство:
Пусть на прямой l 1 отложены равные отрезки A1A2, A2A3, А3А4

и через их концы проведены параллельные прямые, которые пересекают прямую l 2 в точках B1, B2, B3, В4 как рисунке 4. Требуется доказать, что отрезки B1B2, B2B3, В3В4 равны друг другу. Докажем, что B1B2=B2B3.
Рассмотрим случай, когда прямые l 1 и l 2 параллельны. Тогда A1A2=B1B2 и A2A3=B2B3 как противоположные стороны параллелограммов A1B1B2A2 и A2B2B3A3. Так как A1A2= A2A3, то и B1B2=B2B3. Теорема доказана.
Слайд 9 Применение теоремы Фалеса к решению задач
Средняя линия треугольника

Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна ее половине.
Слайд 10Доказательство:
Пусть отрезок DE – средняя линия в треугольнике ABC, т.е. AE = EC,

CD = BD. Проведем через точку D прямую a, параллельную стороне AB. По теореме Фалеса прямая a пересекает сторону AC в ее середине и, следовательно, содержит среднюю линию DE. Значит, средняя линия DE параллельна стороне AB. Проведем среднюю линию DF. Она параллельна стороне AC. Тогда по лемме отрезок ED равен отрезку AF и равен половине отрезка AB. Теорема доказана.
Слайд 11 Задача 1
Дан треугольник АВС. На стороне ВС взята точка Р

так, что ВР=РС, а на стороне АС взята точка Q такая , что АQ : QС = 5 : 3. Найдите отношение АО : ОР, если точка О – точка пересечения прямых АР и ВQ.
Слайд 12 Решение:
Проведем прямые параллельные ВQ через точки А, Р и С.

Точка D – это точка пересечения прямых АР и с.
По теореме Фалеса параллельные прямые ВQ, b и c, которые отсекают равные отрезки ВР и РС, отсекают равные отрезки ОР и РD на прямой АD.
По теореме Фалеса параллельные прямые a, BQ и с, которые отсекают на прямой АС отрезки в соотношении 5 : 3, отсекают и на прямой АD отрезки в соотношении 5 : 3.
То есть AQ : QC= 5:3 и AO : OD = 5:3, а отрезок OD=2OP. Следовательно, AO : OP = 10:3.
Ответ: 10 : 3.
Слайд 13 Задача 2
Разделите отрезок АВ при помощи циркуля и линейки на

n равных частей.
Слайд 14Решение:
Проведем луч AX, не лежащий на прямой AB, и на нем

от точки A отложим последовательно n равных отрезков АА1, А1А2, …,Аn-1An , т.е. на столько равных отрезков, на сколько равных частей нужно разделить данный отрезок AB. Проведем прямую AnB (точка Аn – конец последнего отрезка) и построим прямые, проходящие через точки A1, A2,…, An-1 и параллельные прямые прямой AnB. Эти прямые пересекают отрезок AB в точках B1, B2, …, Bn-1, которые по теореме Фалеса делят отрезок AB на n равных частей.
Слайд 15 Задача 3
Разделите данный отрезок АВ на два отрезка АХ и

ХВ, пропорциональные данным отрезкам P1Q1 и P2Q2.
Слайд 16Решение:
Проведем какой-нибудь луч АМ, не лежащий на прямой АВ, и на

этом луче отложим последовательно отрезки АС и CD, равные отрезкам P1Q1 и P2Q2. Затем проведем прямую BD и прямую, проходящую через точку С параллельно прямой BD. Она по теореме Фалеса пересечет отрезок АВ
в искомой точке Х.















 Государства Ближнего Востока в древности
Государства Ближнего Востока в древности САМОЕ-САМОЕ НА ЗЕМЛЕ!
САМОЕ-САМОЕ НА ЗЕМЛЕ! Forecasting Solutions Project Process
Forecasting Solutions Project Process  Угол здания.
Угол здания. Процесс начисления заработной платы
Процесс начисления заработной платы Экспериментальная работа – основа инновационной и методической работы в школе
Экспериментальная работа – основа инновационной и методической работы в школе Сложение и вычитание двузначных и однозначны чисел
Сложение и вычитание двузначных и однозначны чисел Изображение характера животных на рисунке
Изображение характера животных на рисунке Православное учение о человеке
Православное учение о человеке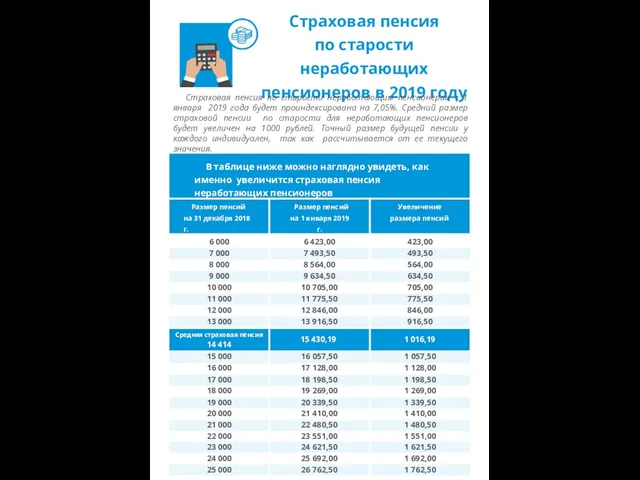 Страховая пенсия по старости неработающих пенсионеров в 2019 году
Страховая пенсия по старости неработающих пенсионеров в 2019 году Голос ребенка в интересах детского сообщества
Голос ребенка в интересах детского сообщества Кинематограф и мультипликация
Кинематограф и мультипликация ФЕДЕРАЛЬНАЯ АНТИМОНОПОЛЬНАЯ СЛУЖБА Вена, 2007 г. Конкурентные аспекты государственного регулирования банковского бизнеса в России.
ФЕДЕРАЛЬНАЯ АНТИМОНОПОЛЬНАЯ СЛУЖБА Вена, 2007 г. Конкурентные аспекты государственного регулирования банковского бизнеса в России. Искусство: что и зачем?
Искусство: что и зачем? Включи свою ідею. Конкурсна робота
Включи свою ідею. Конкурсна робота Концепция создания интеграционной информационной системы «Единое окно по экспортно-импортным операциям»
Концепция создания интеграционной информационной системы «Единое окно по экспортно-импортным операциям»  Самопознание: в стремлении к самосовершенствованию
Самопознание: в стремлении к самосовершенствованию Значение обязательности подготовки граждан к военной службе
Значение обязательности подготовки граждан к военной службе Разработка мероприятия Цифровой текстиль. Синтетические ткани
Разработка мероприятия Цифровой текстиль. Синтетические ткани Меры гарантийной и финансовой поддержки субъектов МСП Ивановским государственным фондом поддержки малого предпринимательства
Меры гарантийной и финансовой поддержки субъектов МСП Ивановским государственным фондом поддержки малого предпринимательства Белсенді саяхат түрлерінде тәсілдік өңдеуді құрудың тәсілі мен
Белсенді саяхат түрлерінде тәсілдік өңдеуді құрудың тәсілі мен Табличный процессор Excel 2007
Табличный процессор Excel 2007 Космический маятник
Космический маятник Заполните таблицу
Заполните таблицу Quality Control System in Germany Система Контроля Качества в Германии Dr. Ulrike Bickelmann Federal Office for Agriculture and Food – Germany Федеральное агентство по сельском
Quality Control System in Germany Система Контроля Качества в Германии Dr. Ulrike Bickelmann Federal Office for Agriculture and Food – Germany Федеральное агентство по сельском Сопротивление движению поезда
Сопротивление движению поезда Презентация на тему Галилеевы спутники Юпитера
Презентация на тему Галилеевы спутники Юпитера ИСТОРИЯ ПРЕДПРИЯТИЯ ТЕХНОЛОГИИ
ИСТОРИЯ ПРЕДПРИЯТИЯ ТЕХНОЛОГИИ