Теорема Фалеса Геометрия, 8 класс

ФАЛЕС (ок. 625 – ок. 547 до н. э.), давньогрецький філософ давньогрецький філософ досократського періоду давньогрецький філософ досократського періоду, математик давньогрецький філософ досократського періоду, математик, астроном, засновник іонійської школи натурфілософії, купець і політичний діяч.
Фалес був першим давньогрецьким філософом і математиком й відтак вважається першим носієм наукової думки в історії[1].
.

Фалес Милетский
З 624 по 547 рік до нашої ери живв Милете.
Син богатого купця, коли він був молодим він багато путешествовал, займався торгівлею, вивчав математику и астрономию , вчився магии у халдеев...
Повернувшись в родной город, Фалес не став витрачати час на торгівлю. Він почав давать совети.

Вообще, Фалесу приписывается масса всевозможных открытий и научных истин. Делать сегодня такие предположения тем более легко, что ни одной строки из сочинений Фалеса никто и никогда не читал. Не исключено, что он вообще ничего не писал. В те годы люди любили это занятие значительно меньше, чем сейчас.

Ми називаем Фалеса вченим тому що, він першим, відмовився від допомоги богів.

Высказывания Фалеса:
"Что прекраснее всего? - Мир, ибо все, что прекрасно устроено, является его частью.
Что мудрее всего? - Время, оно породило одно и породит другое.
Что обще всем? - Надежда: ее имеют и те, у кого нет ничего другого.
Что полезнее всего? - Добродетель, ибо благодаря ей все иное может найти применение и стать полезным.
Что самое вредное? - Порок, ибо в его присутствии портится почти все.
Что сильнее всего? - Необходимость, ибо она непреодолима.
Что самое легкое? - То, что соответствует природе, ибо даже наслаждения часто утомляют"

К сожалению, мудреци смертнітак як, как и всі люди, пусть даже не отмеченные печатью гения. Сохранилось предание, что во время одной из Олимпиад престарелый мудрец, он был, между прочим, страстным болельщиком, взволнованный победой не то сына, не то внука, привстал на скамье, крикнул «слава!» и упал замертво прямо на стадионе. Горожане похоронили Фалеса. Выбили на его гробнице надпись, гласящую: «Насколько мала эта гробница Фалеса, настолько велика слава этого царя астрономов в области звезд».

Фалес также первым узнав всоту одной из египетских пирамид по ее тени. Открыл продолжительность года и разделил его на 365 дней. Его изречение: "Ни за кого не ручайся", которому вторит и Хилон: "Порука и несчастье всегда вместе". Наиболее известное изречение Фалеса: "Соблюдай меру".

Фалесу Милетскому приписывают простой способ определения высоты пирамиды. В солнечный день он поставил свой посох там, где оканчивалась тень от пирамиды. Затем он показал, что как длина одной тени относится к длине другой тени, так и высота пирамиды относится к высоте посоха.

Фалес
Фалес Милетский имел титул одного из семи мудрецов Греции, он был поистине первым философом, первым математиком, астрономом и, вообще, первым по всем наукам в Греции. Он был то же для Греции, что Ломоносов для России.

Фалес на греческой почтовой марке
"Невежество - тяжкое бремя" (Фалес).

Взгляд на развалины Милета

Найдите длину неизвестного отрезка x.

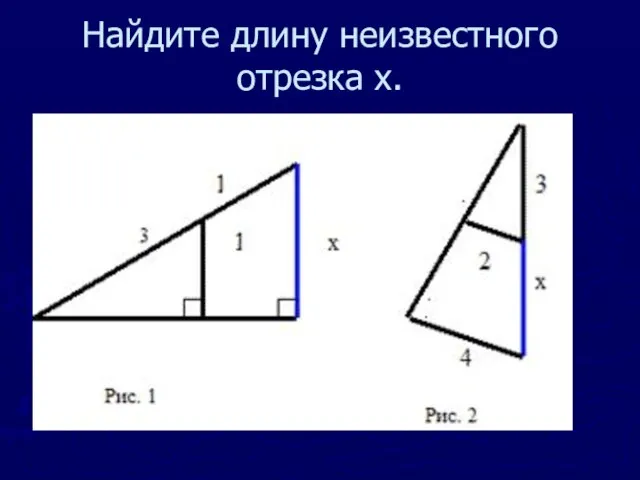
Нахождение расстояния до недоступного предмета.

Но иногда бывает необходимо измерить расстояние и до недоступного предмета. Например, ширину реки. Мы это делаем следующим образом.
Наметив на противоположном берегу реки какой-нибудь четко видимый предмет (А) (дерево, скалу), расположенный у самой воды, надо встать точно напротив него и отметить точку, положив на землю камешек или воткнув колышек (Б). Затем, идя вдоль берега по линии,
перпендикулярной к направлению между предметом на том берегу и колышком, надо отсчитать 30 шагов и воткнуть в землю палку (В). Пройдя в том же направлении еще столько же шагов, снова сделать отметку на земле (Г) и, идя от нее, повернувшись спиной к реке, считать шаги, время от времени поглядывая на намеченный на том берегу предмет. Когда палка В, воткнутая на берегу, окажется на одной линии с предметом А за рекой, то расстояние (Д - Г) от последней отметки до места конечной остановки (Д) будет равно ширине реки.

Определение расстояния построением подобных треугольников
При определении расстояния до недоступных предметов используют различные приемы, связанные с построением подобных треугольников.
Определение расстояния с помощью спички. Спичка - простейший дальномер. Предварительно на ней надо нанести чернилами или карандашом двухмиллиметровые деления. Необходимо также знать примерную высоту предмета, до которого определяется расстояние. Так, рост человека в метрах равен 1,7, колесо велосипеда имеет высоту 0,75, всадник - 2,2, телеграфный столб - 6, одноэтажный дом без крыши - 2,5 - 4 метра.
Допустим, надо определить расстояние до телеграфного столба. Направляем на него спичку на вытянутой руке , длина которой у взрослого человека равна приблизительно 60 см. На спичке изображение столба заняло два деления, то есть 4 миллиметра. На этих данных нетрудно составить такую пропорцию:
длина руки / расстояние до столба = отрезок спички / высота столба = 0,60/Х = 0,004 / 6,0; Х=0,60*6,0/0,004=900
Таким образом, до столба 900 метров.