Теорема Пифагора

Содержание
Формулировка теоремы.
Доказательство.
Формулировка обратной теоремы.
Следствия из теоремы.
Пифагоровы треугольники.
Египетский треугольник.
Различные виды доказательства теоремы.
Литература.

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Формулировка теоремы.
a
b
c

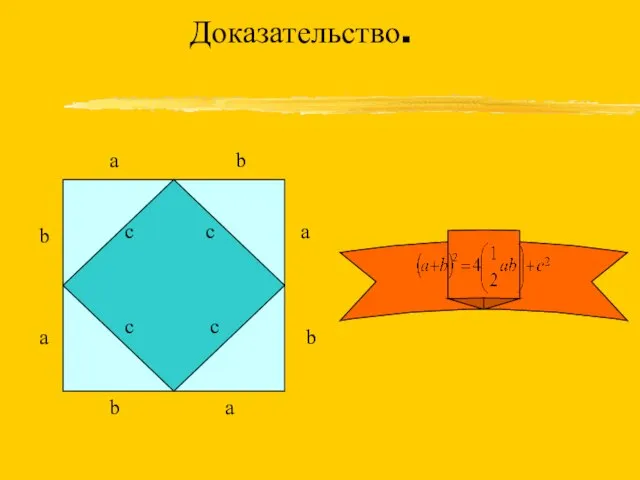
Доказательство.
a
b
c
c
c
c
a
a
a
b
b
b

Формулировка обратной теоремы
Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный.

Следствия из теоремы
В прямоугольном треугольнике любой из катетов меньше гипотенузы.
Косинус любого острого угла меньше 1.
Если к прямой из одной точки проведены перпендикуляр и наклонные, то любая наклонная больше перпендикуляра, равные наклонные имеют равные проекции, из двух наклонных больше та, у которой проекция больше.

Пифагоров треугольник
Прямоугольные треугольники , у которых длины сторон выражаются целыми числами, называются пифагоровыми.
Можно доказать, что катеты a, b и гипотенуза c таких треугольников выражаются формулами a=2m*n, b=m^2-n^2, где m и n – любые натуральные числа ( m>n ).

Египетский треугольник
Землемеры Древнего Египта для построения прямого угла пользовались следующим приемом. Бечевку узлами делили на 12 равных частей и концы связывали. Затем бечевку растягивали на земле так, что получался треугольник со сторонами 3, 4 и 5 делений. Угол треугольника, противолежащий стороне с 5 делениями, был прямой. ( Почему? )
В связи с указанным способом построения прямого угла треугольник со сторонами 3, 4 и 5 единиц иногда называют египетским.

Различные виды доказательства теоремы
В наши дни известно несколько десятков различных доказательств теоремы Пифагора.
Одни из них основаны:
На разбиении квадратов
На дополнении до равных фигур
На том, что высота, опущенная из вершины прямого угла на гипотенузу, делит прямоугольный треугольник на два подобных ему треугольников