Содержание
- 2. Теорема Пифагора Цели: познакомить учащихся с жизнью ученого Пифагора, изложить теорему Пифагора, отработать ее на простых
- 3. ПЛАН 1. Повторение 2. Историческая справка 3.Доказательство теоремы Пифагора 4. Решение задач (по готовым чертежам) 5.
- 4. Чему равна сумма квадратов чисел? а) 32+42 = б) ( )2+ ( )2= 9+16=25 5+7=12
- 5. Верно ли решение? 32+42=(3+4)2 нет
- 6. Чему равно? (а+в)2= а2+2ав+в2
- 7. Какой треугольник изображен на рисунке? Равнобедренный
- 8. Какой треугольник изображен на рисунке? Равносторонний а а а
- 9. Какой треугольник изображен на рисунке? Прямоугольный С
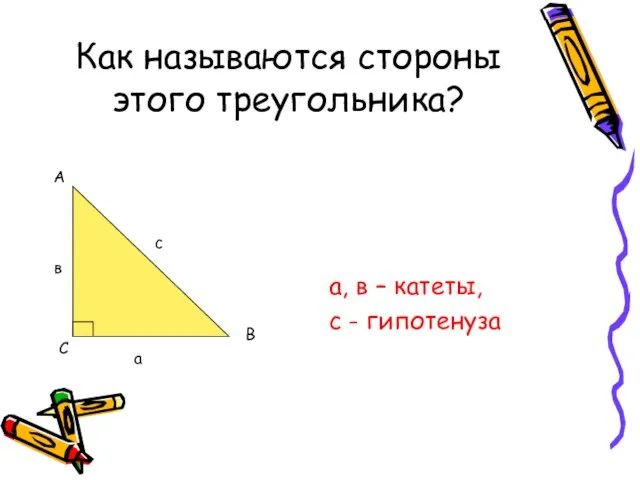
- 10. Как называются стороны этого треугольника? а, в – катеты, с - гипотенуза С с а в
- 11. Найдите площадь треугольника S= (6*8)=24 А С В 6 8
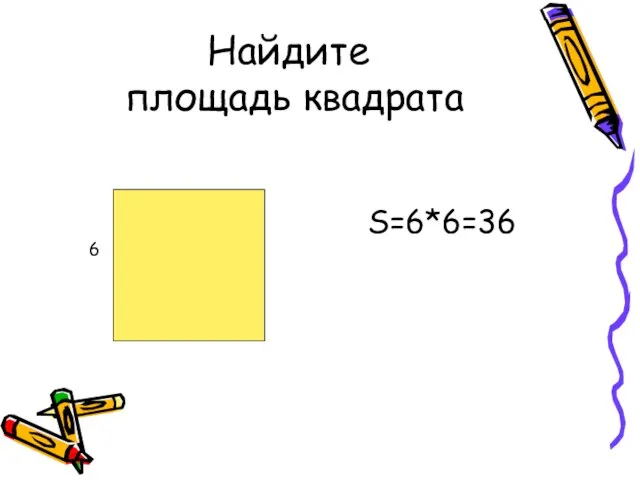
- 12. Найдите площадь квадрата S=6*6=36 6
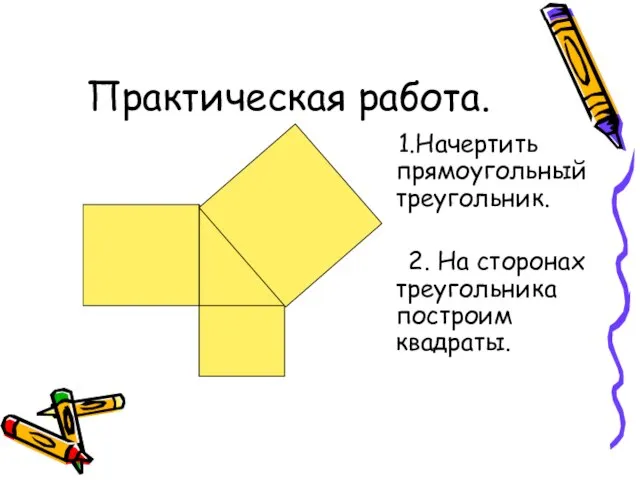
- 13. 1.Начертить прямоугольный треугольник. 2. На сторонах треугольника построим квадраты. Практическая работа.
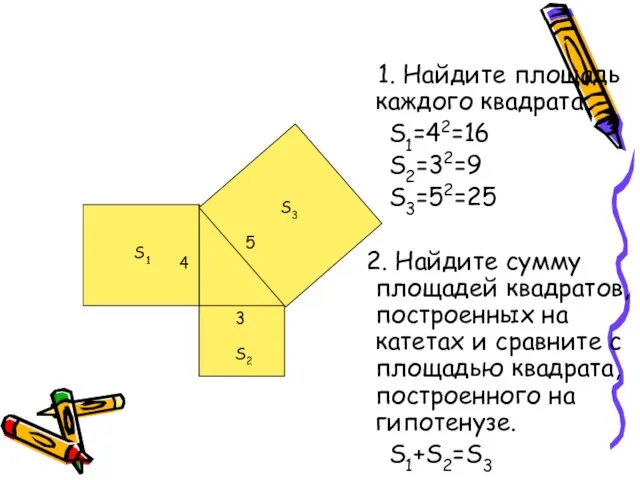
- 14. 1. Найдите площадь каждого квадрата. S1=42=16 S2=32=9 S3=52=25 2. Найдите сумму площадей квадратов, построенных на катетах
- 15. Вывод: Площадь квадрата построенного на гипотенузе прямоугольного треугольника равна сумме площадей квадратов, построенных на катетах.
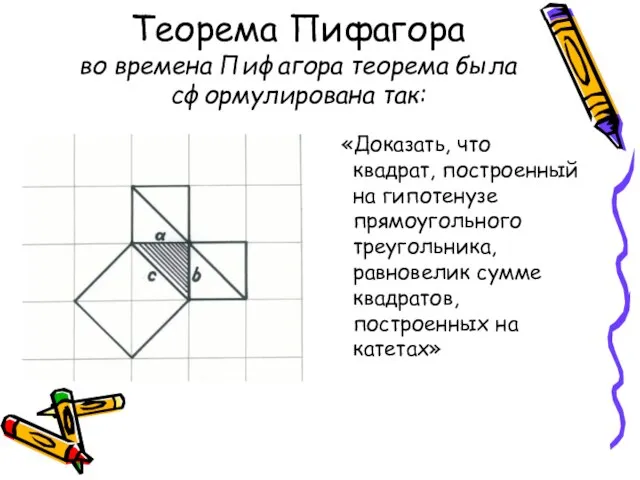
- 16. Теорема Пифагора во времена Пифагора теорема была сформулирована так: «Доказать, что квадрат, построенный на гипотенузе прямоугольного
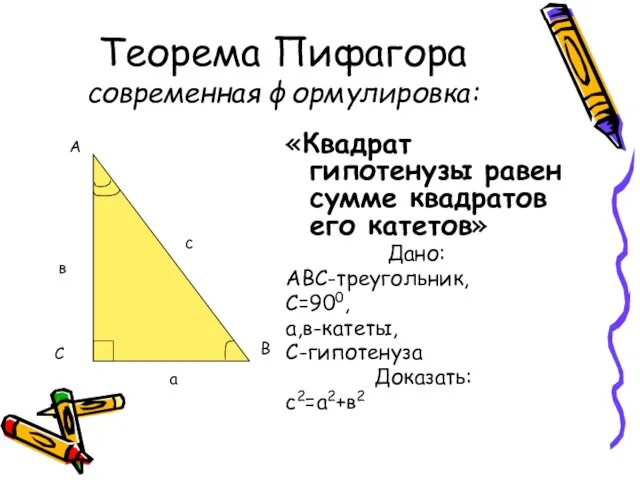
- 17. Теорема Пифагора современная формулировка: «Квадрат гипотенузы равен сумме квадратов его катетов» Дано: АВС-треугольник, С=900, а,в-катеты, С-гипотенуза
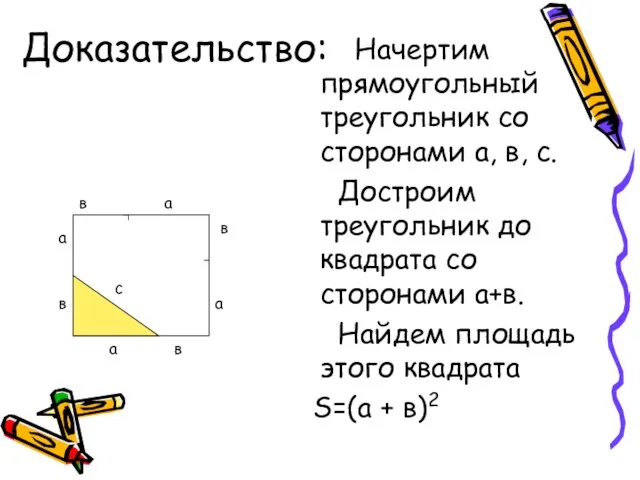
- 18. Начертим прямоугольный треугольник со сторонами а, в, с. Достроим треугольник до квадрата со сторонами а+в. Найдем
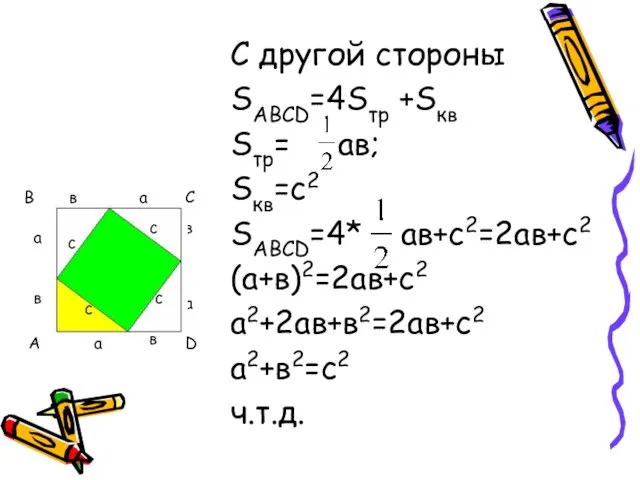
- 19. С другой стороны SABCD=4Sтр +Sкв Sтр= ав; Sкв=c2 SABCD=4* ав+с2=2ав+с2 (а+в)2=2ав+с2 а2+2ав+в2=2ав+с2 а2+в2=с2 ч.т.д. а в
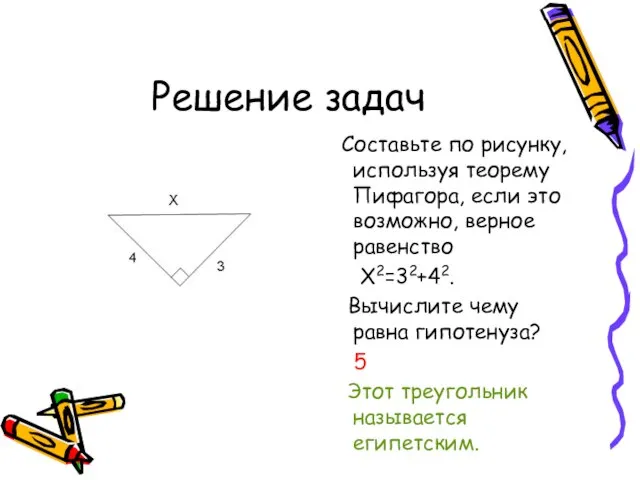
- 20. Решение задач Составьте по рисунку, используя теорему Пифагора, если это возможно, верное равенство Х2=32+42. Вычислите чему
- 21. Можно ли применять теорему Пифагора к этому треугольнику? Нет. Так как этот треугольник не прямоугольный
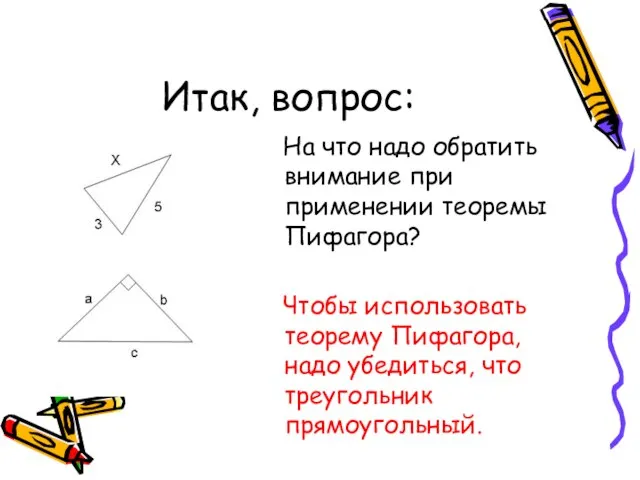
- 22. Итак, вопрос: На что надо обратить внимание при применении теоремы Пифагора? Чтобы использовать теорему Пифагора, надо
- 23. Старинная задача «На берегу реки рос тополь одинокий Вдруг ветра порыв его ствол надломал. Бедный тополь
- 24. Дано: АСД, А=900 АС=3 фута, АD=4 фута. Найти: АВ. Решение АВ=АС+СD. По теореме Пифагора CD2=AC2+CD2, СD2=
- 25. Домашнее задание Пункт 54. №483 (б), №484 (в)
- 27. Скачать презентацию



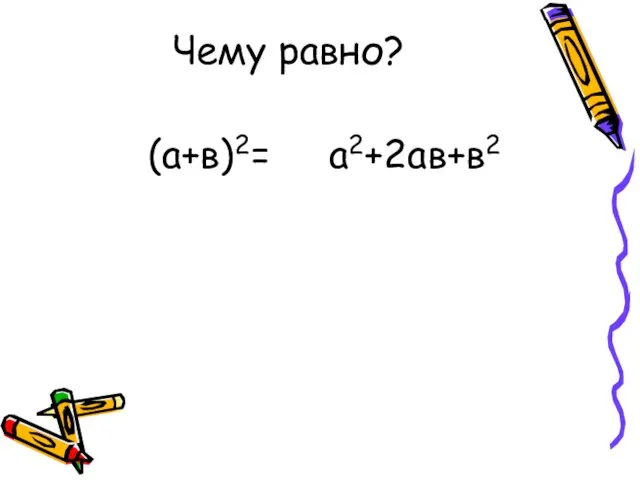









 В. Гинуков. Условный портрет автора Слова
В. Гинуков. Условный портрет автора Слова Кафедра естественных наук
Кафедра естественных наук 249175
249175 Голосовой помощник Маруся
Голосовой помощник Маруся Девять предметов в системе счисления
Девять предметов в системе счисления Саморегулирующиеся организации «СРО Телеком» и СРО Телеком-Про»
Саморегулирующиеся организации «СРО Телеком» и СРО Телеком-Про» «Страницы семейного архива»
«Страницы семейного архива» Статистика терроризма
Статистика терроризма Социальные, этнические, конфессиональные и культурные различия личности
Социальные, этнические, конфессиональные и культурные различия личности Опиливание заготовок из сортового проката.Резание металла слесарной ножовкой.
Опиливание заготовок из сортового проката.Резание металла слесарной ножовкой. Гай Юлий Цезарь
Гай Юлий Цезарь Презентация на тему Новогодние игры со Снегурочкой и Дедом Морозом
Презентация на тему Новогодние игры со Снегурочкой и Дедом Морозом Презентация на тему Ёлочка из перьев
Презентация на тему Ёлочка из перьев Структура спонсорского пакета для чемпионата Санкт-Петербурга по водному поло.u
Структура спонсорского пакета для чемпионата Санкт-Петербурга по водному поло.u Заголовок Название раздела 1 Ленвендо Кто мы www.lenvendo.ru.
Заголовок Название раздела 1 Ленвендо Кто мы www.lenvendo.ru. ПОЛЯРИЗАЦИЯ И ДИФРАКЦИЯ СВЕТА
ПОЛЯРИЗАЦИЯ И ДИФРАКЦИЯ СВЕТА Тема урока: «Тайны поэзии Н.Гумилева»
Тема урока: «Тайны поэзии Н.Гумилева» Презентация на тему Лингвистический проект
Презентация на тему Лингвистический проект Цифровые автоматы, кодирование сигнала
Цифровые автоматы, кодирование сигнала Самодержавие Алексея Михайловича Тишайшего
Самодержавие Алексея Михайловича Тишайшего Презентация на тему Рулевое управление автомобиля
Презентация на тему Рулевое управление автомобиля Евгений Замятин. Роман-антиутопия "Мы“ как предупреждение потомкам
Евгений Замятин. Роман-антиутопия "Мы“ как предупреждение потомкам Модель управления имущественными комплексами вузов и вопросы распоряжения имуществом
Модель управления имущественными комплексами вузов и вопросы распоряжения имуществом Техника построения эллипсов во фронтальной плоскости проекций
Техника построения эллипсов во фронтальной плоскости проекций Нательные кресты XI – конца XIX вв. в экспозиции музея им. 1000-летия Брянска
Нательные кресты XI – конца XIX вв. в экспозиции музея им. 1000-летия Брянска Запатентован первый кассовый аппарат (1879)
Запатентован первый кассовый аппарат (1879) Система права
Система права Тест по рыбе
Тест по рыбе