Содержание
- 2. Тема урока: «Теорема Пифагора и способы её доказательства» Цель урока: Проверить уровень теоретических знаний по теме
- 3. Учебные материалы Атанасян Л.С., В.Ф. Бутузов и другие «Геометрия 7-9» А.Я.Кононов «Устные занятия по математике» Рязановский
- 4. Ход урока Организационный момент Проверка усвоения темы «Площадь многоугольника». (Тестирование) Объяснение новой темы Закрепление Домашняя работа
- 5. II.Проверка домашней работы Устный опрос: Существует ли формула для вычисления площади произвольного четырехугольника? Какие способы вычисления
- 6. Пифагор Пребудет вечной истина, как скоро Ее познает слабый человек! И ныне теорема Пифагора Верна, как
- 7. Биография Пифагора Великий ученый Пифагор родился около 570 г. до н.э. на острове Самосе. Отцом Пифагора
- 8. Теорема Пифагора Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на катетах…
- 9. О теореме Пифагора… Это одна из самых известных геометрических теорем древности, называемая теоремой Пифагора. Её и
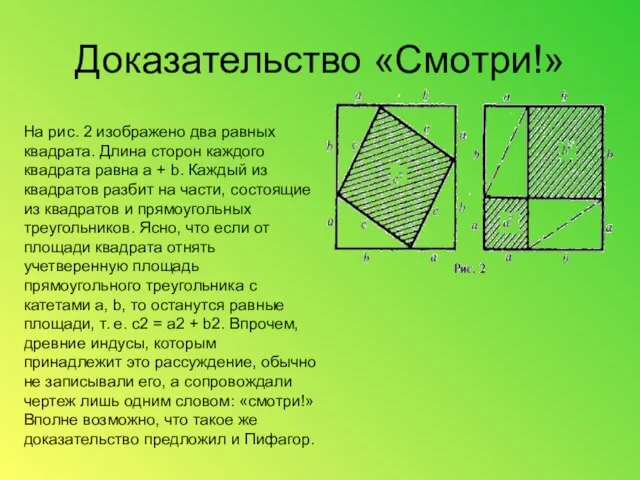
- 10. Доказательство «Смотри!» На рис. 2 изображено два равных квадрата. Длина сторон каждого квадрата равна a +
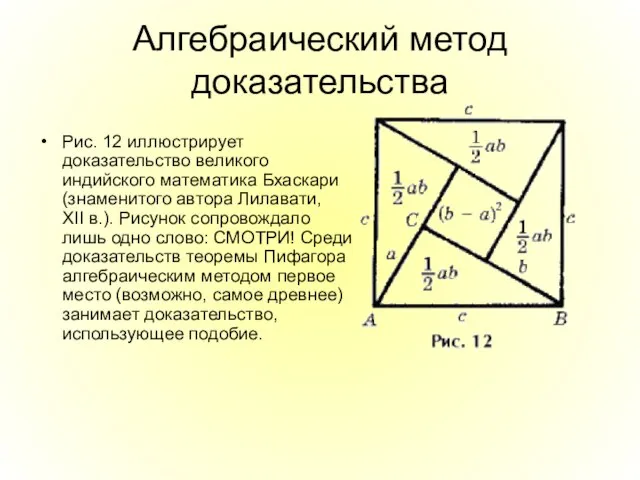
- 11. Алгебраический метод доказательства Рис. 12 иллюстрирует доказательство великого индийского математика Бхаскари (знаменитого автора Лилавати, XII в.).
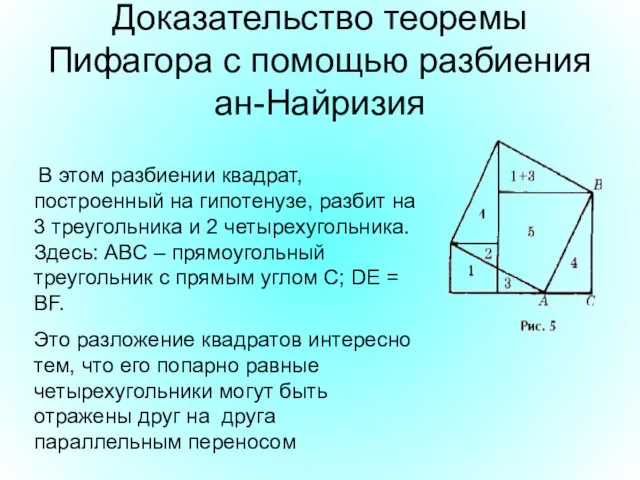
- 12. Доказательство теоремы Пифагора с помощью разбиения ан-Найризия В этом разбиении квадрат, построенный на гипотенузе, разбит на
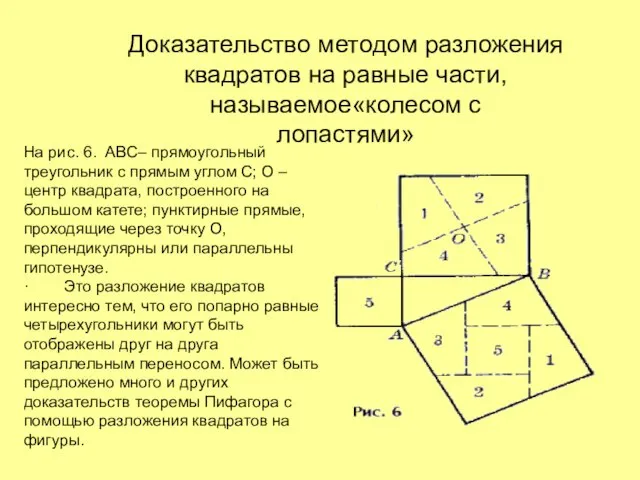
- 13. Доказательство методом разложения квадратов на равные части, называемое«колесом с лопастями» На рис. 6. ABC– прямоугольный треугольник
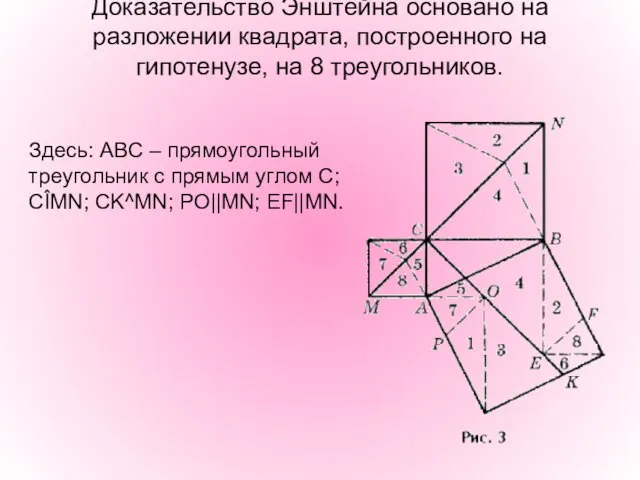
- 14. Доказательство Энштейна основано на разложении квадрата, построенного на гипотенузе, на 8 треугольников. Здесь: ABC – прямоугольный
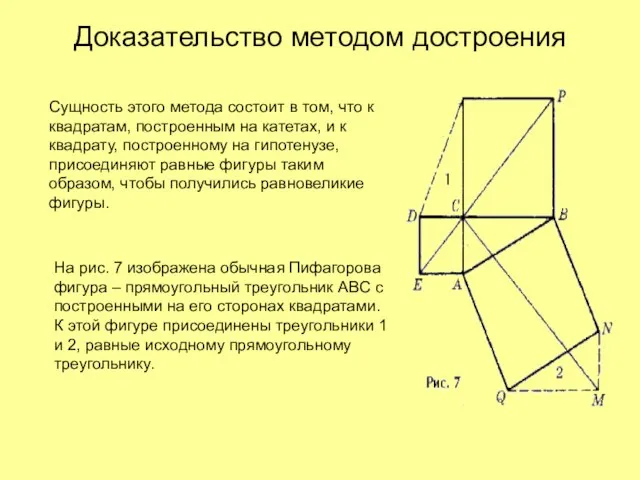
- 15. Доказательство методом достроения Сущность этого метода состоит в том, что к квадратам, построенным на катетах, и
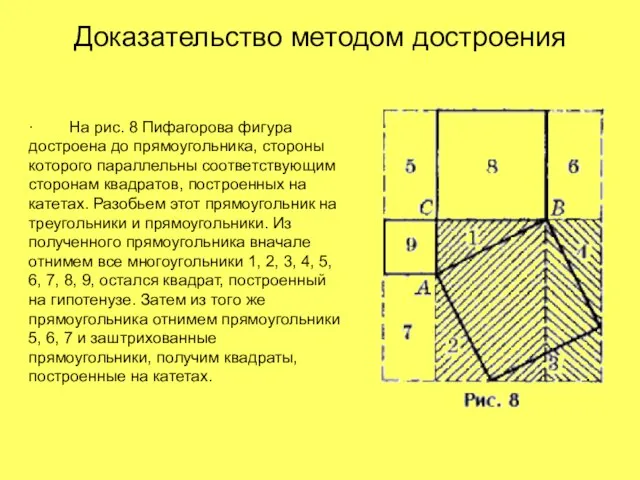
- 16. Доказательство методом достроения · На рис. 8 Пифагорова фигура достроена до прямоугольника, стороны которого параллельны соответствующим
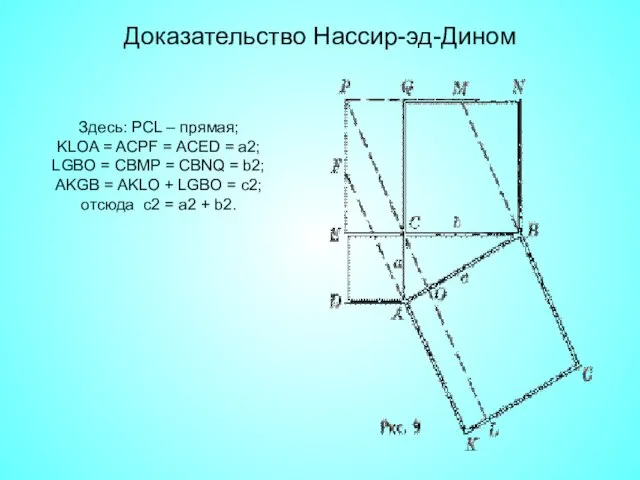
- 17. Доказательство Нассир-эд-Дином Здесь: PCL – прямая; KLOA = ACPF = ACED = a2; LGBO = CBMP
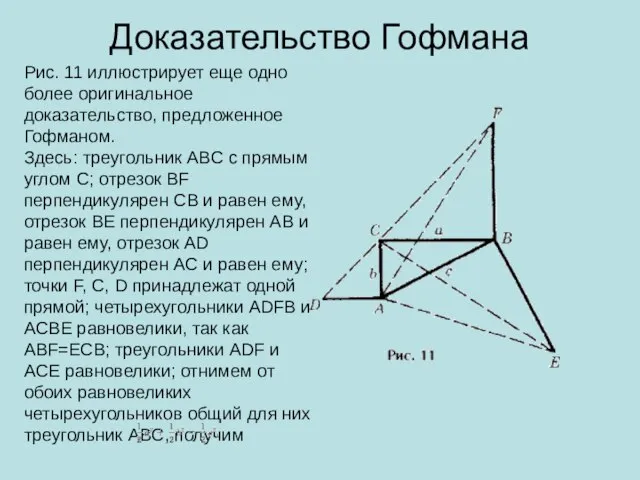
- 18. Доказательство Гофмана Рис. 11 иллюстрирует еще одно более оригинальное доказательство, предложенное Гофманом. Здесь: треугольник ABC с
- 19. IV.Закрепление. Решение задач Задача 1. Дано: АВС- равнобедренный треугольник АВ=ВС=17 см, АС=16 см, ВD- высота Найти:
- 21. Скачать презентацию









 Ты, человек, любя природу,Хоть иногда её жалей:В увеселительных походахНе растопчи её полей.В вокзальной сутолоке векаТы оценит
Ты, человек, любя природу,Хоть иногда её жалей:В увеселительных походахНе растопчи её полей.В вокзальной сутолоке векаТы оценит NXP semiconductors, Москва. Краткий обзор
NXP semiconductors, Москва. Краткий обзор Однофазный TIG-инвертор
Однофазный TIG-инвертор Індекси цін у будівництві
Індекси цін у будівництві Банки и банковская система РФ. Тест
Банки и банковская система РФ. Тест Прикладной Тайм-менеджмент для программистов
Прикладной Тайм-менеджмент для программистов ГПОУ Горловский автотранспортный техникум. ГОУВПО Донецкий национальный технический университет
ГПОУ Горловский автотранспортный техникум. ГОУВПО Донецкий национальный технический университет Кабинет министров
Кабинет министров Республиканский научно-исследовательский институт интеллектуальной собственности ул. Б.Якиманка, д. 38, г. Москва, 119049 тел./факс: +
Республиканский научно-исследовательский институт интеллектуальной собственности ул. Б.Якиманка, д. 38, г. Москва, 119049 тел./факс: + Доброволец на ЧС. Особенности психологической устойчивости личного состава. Способы подготовки
Доброволец на ЧС. Особенности психологической устойчивости личного состава. Способы подготовки Сессия Госконтроль 2.0: образ будущего
Сессия Госконтроль 2.0: образ будущего Презентация Microsoft PowerPoint
Презентация Microsoft PowerPoint Перпендикуляр и наклонные
Перпендикуляр и наклонные Однородные члены предложения
Однородные члены предложения Предмет, метод, источники и принципы Трудового права
Предмет, метод, источники и принципы Трудового права Поэты Ставрополья о родном крае и о природе родного края
Поэты Ставрополья о родном крае и о природе родного края Педагогический совет «Поиск путей совершенствования образовательной среды школы при введении федерального государственного обр
Педагогический совет «Поиск путей совершенствования образовательной среды школы при введении федерального государственного обр Обзор на персонажа
Обзор на персонажа ВКР: Действительный цикл машины МВВ6 - 1 -2
ВКР: Действительный цикл машины МВВ6 - 1 -2 15 февраля 1861 года родился швейцарский физик-метролог Шарль Эдуард Гильом (Гийом).
15 февраля 1861 года родился швейцарский физик-метролог Шарль Эдуард Гильом (Гийом). Правила наложения жгутов повязок и шин
Правила наложения жгутов повязок и шин Вальдорфская система образования
Вальдорфская система образования Social Ecology Sustainable Development
Social Ecology Sustainable Development  Ваш профессиональный маршрут
Ваш профессиональный маршрут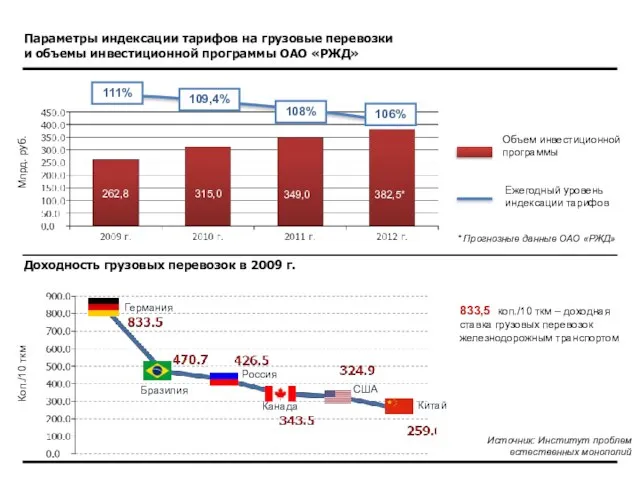 Параметры индексации тарифов на грузовые перевозки и объемы инвестиционной программы ОАО «РЖД»
Параметры индексации тарифов на грузовые перевозки и объемы инвестиционной программы ОАО «РЖД» Концепция воспитательной системы
Концепция воспитательной системы Технология создания и редактирования изображений в векторном редакторе
Технология создания и редактирования изображений в векторном редакторе Презентация на тему Использования краеведческого материала в образовательном процессе
Презентация на тему Использования краеведческого материала в образовательном процессе