Teoria_algoritmov

СОДЕРЖАНИЕ
Введение 1
Эффективность алгоритмов 2
Разработка алгоритмов 3
Машина Тьюринга 4
Рекурсивные функции 5
26.09.2022
ТЕОРИЯ АЛГОРИТМОВ

Введение
История возникновения;
Модели вычислений;
Направления.
ТЕОРИЯ АЛГОРИТМОВ
АЛАН ТЬЮРИНГ (1912-1954)

Введение
Актуальность - проникновение понятия "алгоритм" в различные сферы жизни человека.
Заинтересовало то, что в нашей повседневной жизни нас окружают алгоритмы, любой человек выполняет свои действия по порядку, раздумывая, правильно ли он поступает.
ТЕОРИЯ АЛГОРИТМОВ

Введение
Алгоритм – является достаточно точной инструкцией, характеризующих очередность взаимодействий исполнителя для достижения результата урегулирования задачи за итоговое время.
ТЕОРИЯ АЛГОРИТМОВ

ЭФФЕКТИВНОСТЬ АЛГОРИТМОВ
Способы достижения эффективности алгоритмов.

Эффективность алгоритмов
Способы достижения эффективности алгоритмов:
Наличие начальных данных и некоторого результата;
Форма алгоритмов;
Алгоритмические структуры (типы алгоритмов)
ТЕОРИЯ АЛГОРИТМОВ

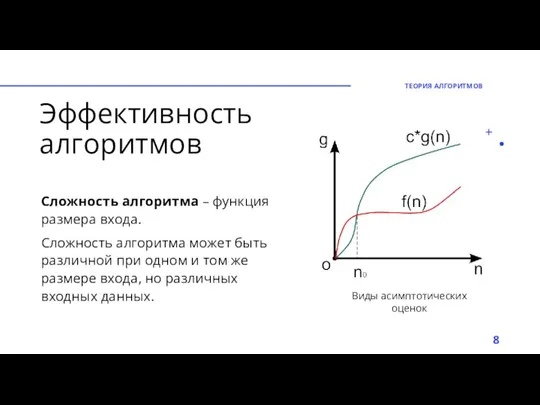
Эффективность алгоритмов
Сложность алгоритма – функция размера входа.
Сложность алгоритма может быть различной при одном и том же размере входа, но различных входных данных.
ТЕОРИЯ АЛГОРИТМОВ
Виды асимптотических оценок

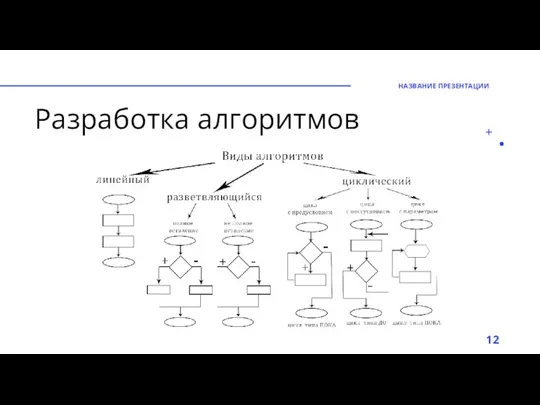
РАЗРАБОТКА АЛГОРИТМОВ
Линейные алгоритмы

Разработка алгоритмов
Массовость алгоритма – это свойство заключается в том, что каждый алгоритм, разработанный для решения некоторой задачи, должен быть применен для решения задач данного типа при всех допустимых значениях исходных данных.
ТЕОРИЯ АЛГОРИТМОВ

Разработка алгоритмов
Любые вычислительные процессы, производимые на электронной вычислительной машине по заданной программе, возможно разделить на три основные части:
Прямые;
Не прямые;
Повторяющиеся.
ТЕОРИЯ АЛГОРИТМОВ

Разработка алгоритмов
НАЗВАНИЕ ПРЕЗЕНТАЦИИ

МАШИНА ТЬЮРИНГА
Устройство машины тьюринга

Машина Тьюринга
В состав машины Тьюринга вмещается нескончаемая в обе края лента (возможны машины Тьюринга, которые располагают немного не иссякающих лент), разделённая на ячейки, и управляющее устройство, способное пребывать в одном из множества состояний. Число вероятных состояний управляющего устройства конечно и точно задано.
ТЕОРИЯ АЛГОРИТМОВ

Машина Тьюринга
Машина Тьюринга может рассматриваться как распознаватель определенного языка ?, если она завершает работу в дозволяющем состоянии, имеясь заброшенной на тех и только на тех словах, которые относятся к этому языку
ТЕОРИЯ АЛГОРИТМОВ

РЕКУРСИВНЫЕ ФУНКЦИИ
Определение, происхождение

Рекурсивные функции
Рекурсия
Метод решения вычислительной задачи, решение которого зависит от решений более мелких экземпляров той же задачи.
Рекурсия решает рекурсивные проблемы, используя функции, которые вызывают сами себя из своего собственного кода.
Происхождение
Начало рекурсивных функций берут из циклического вызова функций в алгоритме.
Выбирались простые функции для вычисления точных результатов, после чего на новых функционалах использовались уже имеющиеся алгоритмы.