Теорiя iгор

Зміст
Предмет ТІ
ВИЗНАЧЕННЯ
4 групи ТІ
Статистичні ігри
Критерії Байєса
Критерій Бернуллі-Лапласа
Критерій Вальда
Критерій Гермеєра
Критерій крайнього оптимізму - максимакс
Критерій Севіджа (КС)
Критерій Гурвіца (КГ)
Критерій Ходжеса-Лемана
ВИСНОВКИ

Предмет теорії ігор
Математичний апарат для вибору стратегії в конфліктних ситуаціях, дає можливість краще зрозуміти конкурентне середовище і звести до мінімуму ступінь ризику
Аналіз ризикової ситуації за допомогою ТІ спонукає підприємця (менеджера) розглядати всі можливі альтернативи як своїх дій, так і стратегії конкурентів і партнерів
Адам Сміт – “мотивація гравця – це властива більшості людей самонадіяна переоцінка своїх здібностей і абсурдна віра у свою щасливу зірку”
Джон Кейнс – “якщо б людині по своїй природі не властива була б спокуса використати свій шанс… то на долю одного лише холодного розрахунку припало б не так багато інвестицій”
1944 – монографія Дж. фон Неймана і О. фон Моргенштерна “Теорія ігор і економічної поведінки”

ВИЗНАЧЕННЯ
ГРА – формалізований опис (модель) конфліктної ситуації, що містить чітко визначені правила дій її учасників, які намагаються отримати певну перемогу через вибір конкретної (в певному розумінні найкращої) стратегії поведінки
ТЕОРІЯ ІГОР – це розділ сучасної математики (теорія математичних моделей прийняття оптимальних рішень), в якому вивчають математичні моделі прийняття рішень за умов, коли інтереси сторін (гравців, учасників) різні або протилежні (за умов конфліктності), причому вони досягають своєї мети різними шляхами

Невизначеність результату гри зумовлена різними причинами, які можна поділити на 4 групи
Комбінаторні ігри. Особливості правил гри зумовлюють таку множину варіантів її розвитку, що передбачити результати гри заздалегідь неможливо (шахи)
Азартні ігри. Джерело невизначеності – є вплив випадкових чинників (кості, рулетка...)
Стратегічні ігри. Невизначеність зумовлюється відсутністю інформації про дії та стратегію супротивника (гра двох осіб з нульовою сумою – сума виграшів сторін=0:мета одного – максимізувати свій виграш, другого – мінімізувати програш)
Ігри з природою. Невизначеність зумовлюється не свідомими діями інших гравців, а відсутністю інформації про умови, в яких здійснюється дія (об’єктивна дійсність-природа)

ВИЗНАЧЕННЯ
ГРАВЕЦЬ – суб’єкт прийняття рішення (конфліктуючі сторони)
ПЛАТІЖНА ФУНКЦІЯ – цільова функція
СТРАТЕГІЯ ГРАВЦЯ – план (рішення), відповідно до якого гравець здійснює вибір своєї дії у будь-якій можливій ситуації і при будь-якій можливій фактичній інформації
МЕТА ГРИ – виграш одного з партнерів з врахуванням відповідних дій партнера (суперника)
ПРАВИЛА ГРИ – визначають можливі варіанти дій гравців, обсяг інформації кожної сторони про дії іншої, результат гри, до якого приводить відповідна послідовність ходів
ХІД ГРИ – вибір однієї з допустимих правилами гри дій і її здійснення

ВИЗНАЧЕННЯ
ОПТИМАЛЬНА СТРАТЕГІЯ – стратегія, яка при багаторазовому повторенні гри забезпечує даному гравцю максимально можливий середній виграш

Статистичні ігри -
Один учасник – людина (група), об’єднана одною метою, інший – зовнішнє середовище
(гравець А – “статистик”, гравець Е – “природа” – весь комплекс зовнішніх умов, за яких статистик вимушений приймати рішення. “Природа”(економіка) байдужа до виграшу і не прагне використати на свою користь похибки “статистика”)

Статистичні ігри
“Статистик” може використовувати m стратегій А1....Аm, а природа може реалізовувати n різних середовищ Е1...Еn. “Статистику” можуть бути відомі ймовірності pj, з якими природа реалізує свої становища Еj. Діючи проти природи, “статистик” може використовувати як чисті стратегії Аі, так і змішані q=(q1,…,qm). Якщо “статистик” має змогу кількісно оцінити (величиною aij) наслідки використання кожної своєї чистої стратегії Аі при будь-якому становищі природи Ej, то гру можна задати платіжною матрицею (табл.)
При спрощенні платіжної матриці статистичної гри не можна ігнорувати ті чи інші стани природи (стратегії гравця Е), бо вона може реалізувати будь-який свій стан незалежно від того вигідно це “статистику” чи ні.

Платіжна матриця – табл.1

ОСОБЛИВОСТІ
Гравець “природа” не вибирає оптимальної стратегії, але “статистик” повинен прагнути до визначення розподілу ймовірностей станів “природи”. Статистичні ігри мають певні відмінності від стратегічних:
Відсутність прагнення до виграшу у гравця “природа”, тобто відсутність антагоністичного супротивника
Можливість “статистика” провести статистичний експеримент для отримання додаткової інформації про стратегії “природи”.

Матриця ризиків
При виборі оптимальної стратегії “статистик” використовує різні критерії, спираючись як на платіжну матрицю, так і на матрицю ризиків. Ризиком rij “статистика” при використанні ним чистої стратегії Аі і стану “природи” Еj називається різниця між максимальним виграшем
(мінімальними збитками чи витратами - ), який він міг би отримати, якби з цілковитою впевненістю знав, що “природою” буде реалізовано дійсно стан Еj , і тим виграшем aij, який він одержить, використовуючи стратегію Аі, не знаючи який стан Еj “природа” реалізує.

Матриця ризиків
Отже, елементи rij матриці ризиків (табл.2) визначаються за формулою
Максимально можливий виграш “статистика” при стані Еj (максимальний елемент j-го стовпця платіжної матриці), тобто
За умови, що платіжна матриця складена по даних про витрати, елементи rij матриці ризиків визначаються за формулою:

Платіжна матриця – табл.2

Ймовірність відома
Якщо ймовірності pj станів Ej “природи” відомі, то використовують критерії Байєса і Бернуллі-Лапласа.

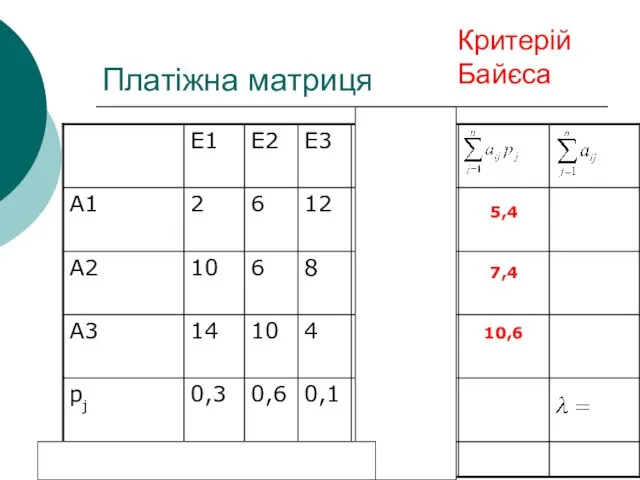
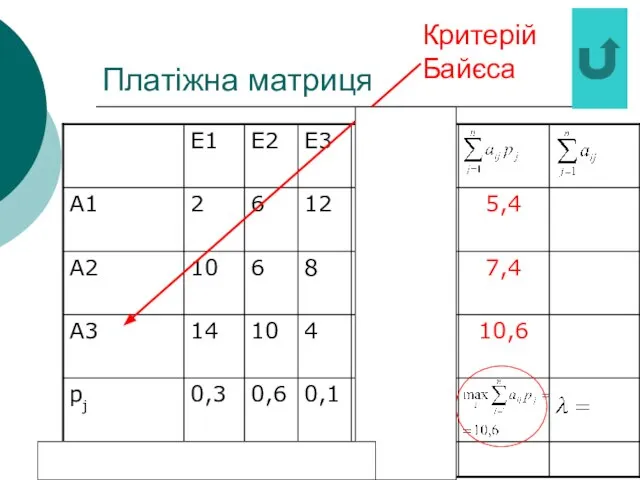
Критерій Байєса
За оптимальну за критерієм Байєса обирається чиста стратегія Ai, за якої максимізується середній виграш “статистика” , тобто забезпечується
якщо платіжна матриця складена по даних про витрати

Критерій Бернуллі-Лапласа
Якщо “статистик” вважає рівноцінно ймовірними всі стани “природи Ej (p1=…=pj=…=pn=1/n), то оптимальною за критерієм Бернуллі-Лапласа, вважається чиста стратегія Аі, яка забезпечує
Критерій Бернуллі-Лапласа називають принципом недостатнього обґрунтування

Ймовірність невідома
Якщо ймовірність pj станів “природи” Ej невідома, то використовують критерії Вальда, Севіджа, Гурвіца.

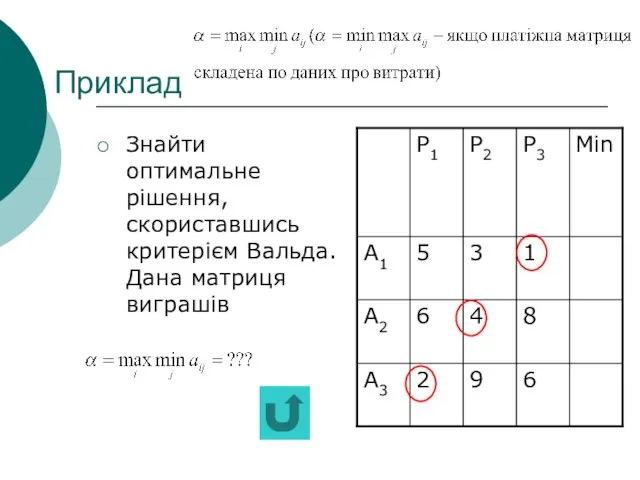
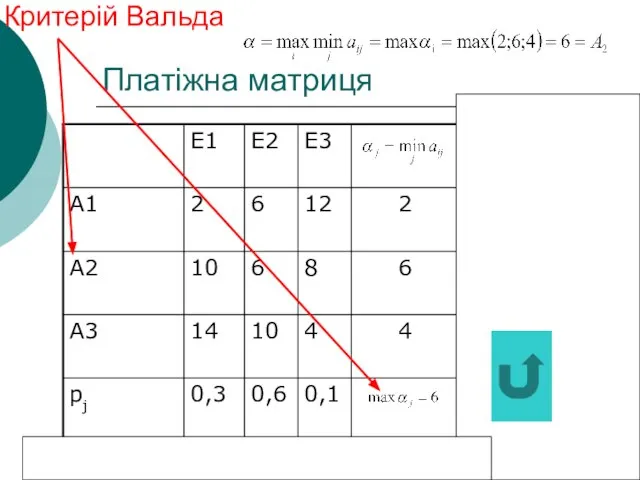
Критерій Вальда
Оптимальною вважається чиста стратегія Ai, при якій найменший виграш “статистика” буде максимальним, тобто йому забезпечується максимін
КВ використовують у випадках коли необхідна гарантія, щоб виграш за будь-яких умов був не менший, чим найбільший із можливих за гірших умов

Приклад
Знайти оптимальне рішення, скориставшись критерієм Вальда. Дана матриця виграшів

Критерій Гермеєра
Для змішаних стратегій КВ перетворюється на критерій Гермеєра і формулюється так: оптимальною вважається та змішана стратегія, за якої мінімальний середній виграш “статистика” буде максимальним, тобто стратегія q*, знайдена з умови

Критерій крайнього оптимізму - максимакс
“Статистик” передбачає, що “природа” буде перебувати у найсприятливішому для нього стані. Оптимальною за максимаксним критерієм вважається чиста стратегія Аі, при якій найбільший виграш “статистика” буде максимальним, тобто йому забезпечується максимакс
Виграшу “статистика” відповідатиме найбільший (найменший) елемент платіжної матриці

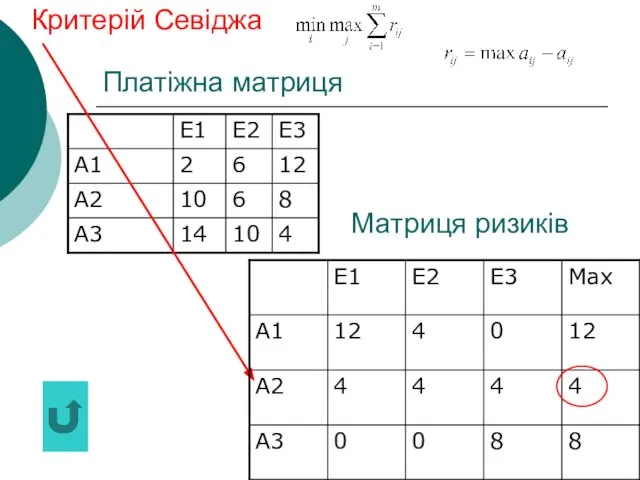
Критерій Севіджа (КС)
Оптимальною вважається чиста стратегія Аі, при якій мінімізується величина максимального ризику, тобто забезпечується
Для змішаних стратегій КС формулюється так: оптимальною вважається та змішана стратегія, за якої максимальний середній ризик “статистика” мінімізується, тобто стратегія q*, знайдена з умови

Приклад
Знайти оптимальне рішення, скориставшись критерієм Севіджа, якщо відома матриця прибутку
Тепер будуємо матрицю втрат
7
5
4

Д/з
Знайти оптимальне рішення, скориставшись критерієм Севіджа, якщо відома матриця збитків

Критерій Гурвіца (КГ)
Оптимальною вважається чиста стратегія Аі, знайдена з умови
або
Де - вибирається суб’єктивними міркуваннями і називається показником песимізму

2 підходи для пошуку оптимальної стратегії за КГ
Знаходять рекомендовані стратегії за умов оптимізму і песимізму . Якщо в обох випадках отримана одна стратегія, то вона є оптимальною. Якщо дві – на основі схильності (несхильності) гравця до ризику формується чиста (песимістична або оптимістична) або змішана стратегія
Розглядають крайні варіанти (оптимізму к=0 і песимізму к=1). Якщо розрахунки пропонують дві стратегії, то визначають момент зміни стратегій, прирівнявши вирази за ними
І розв’язують рівняння щодо к

Критерій Ходжеса-Лемана
Поєднання критеріїв Байєса і Вальда за допомогою параметра
:
Оптимальною вважається стратегія, що відповідає умові
Критерій Вальда
Критерій Байєса

Приклад
Підприємство планує випускати новий вид продукції. За оцінками експертів воно може опинитися в одній з трьох можливих ситуацій:
1) виникне додаткова потреба в уже існуючій продукції
2) з”явиться необхідність оновлення існуючої продукції
3) постане необхідність розробки нової продукції
Досвід роботи підприємства свідчить, що ймовірність розглянутих станів відповідно становить: 0,3; 0,6; 0,1. Залежно від ситуації, що виникає на ринку, керівництво підприємства може прийняти такі рішення:
1) збільшити випуск існуючої продукції;
2) оновити асортимент існуючої продукції власними силами;
3) укласти договір на розробку і постачання технології з іншим підприємством.
Можливі прибутки відповідно до обраних стратегій становлять:
2 6 12
10 6 8
14 10 4

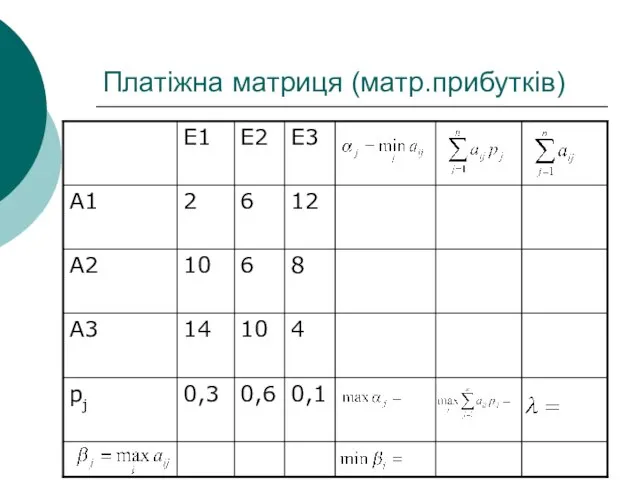
Розв”язок
У цій ситуації “статистиком” є керівництво підприємства, яке висуває три стратегії: А1,А2, А3. Другим гравцем є “природа” = комплекс зовнішніх ринкових умов, в яких функціонує підприємство. Існує три можливі стани “природи” – Е1, Е2, Е3. Виграшами “статистика” А буде прибуток за стратегіями А1,А2, А3

Платіжна матриця (матр.прибутків)

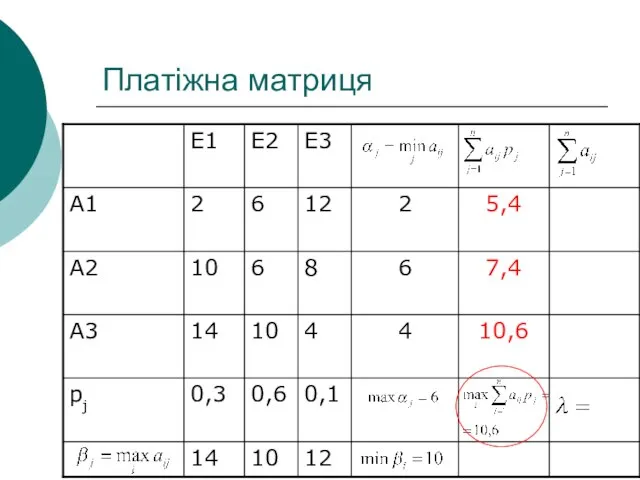
Платіжна матриця
Критерій Байєса
5,4
7,4
10,6

Платіжна матриця
Критерій Байєса

Платіжна матриця

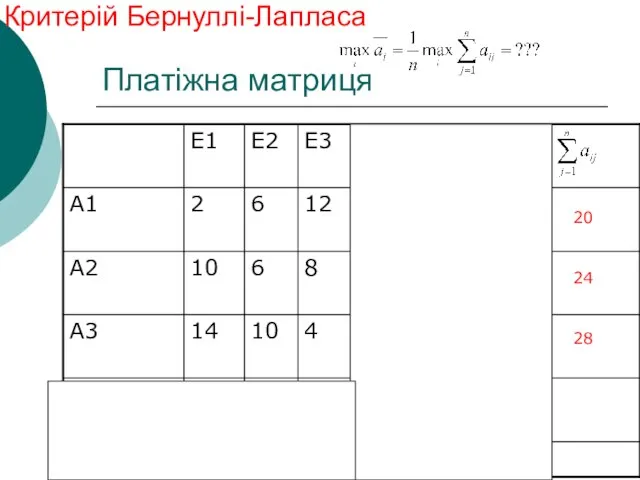
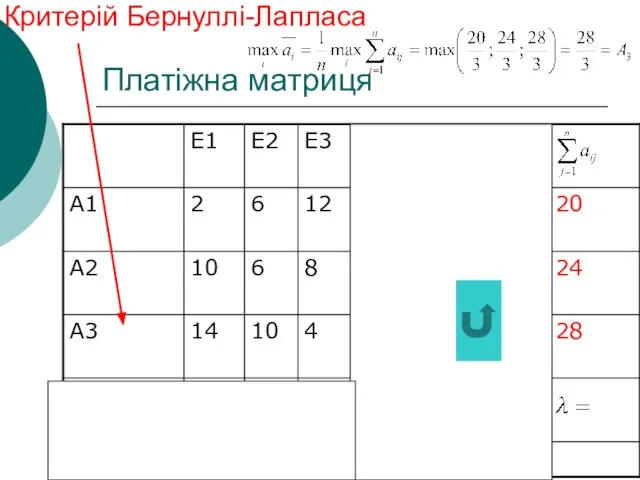
Платіжна матриця
Критерій Бернуллі-Лапласа
20
24
28

Платіжна матриця
Критерій Бернуллі-Лапласа

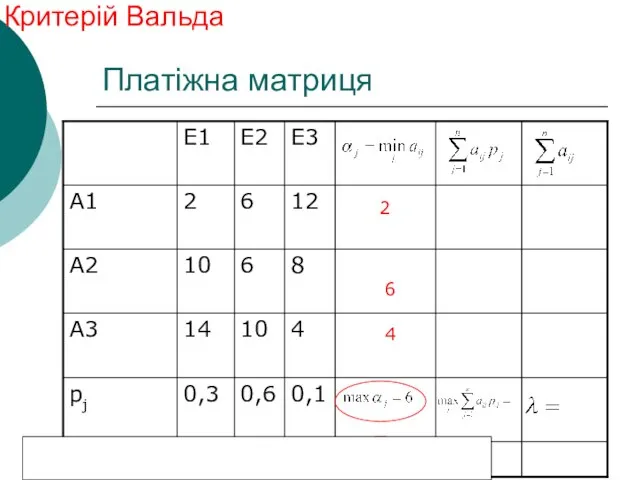
Платіжна матриця
Критерій Вальда
2
6
4

Платіжна матриця
Критерій Вальда

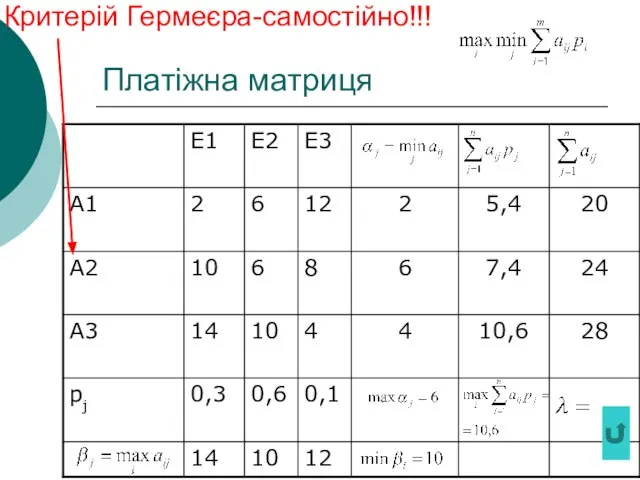
Платіжна матриця
Критерій Гермеєра-самостійно!!!

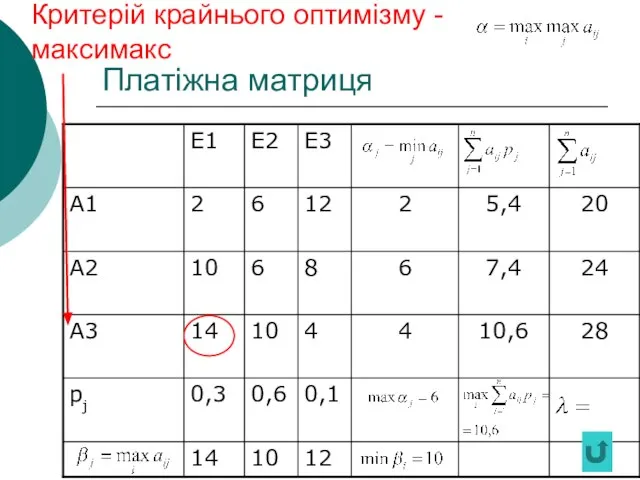
Платіжна матриця
Критерій крайнього оптимізму - максимакс

Платіжна матриця
Критерій Севіджа
Матриця ризиків

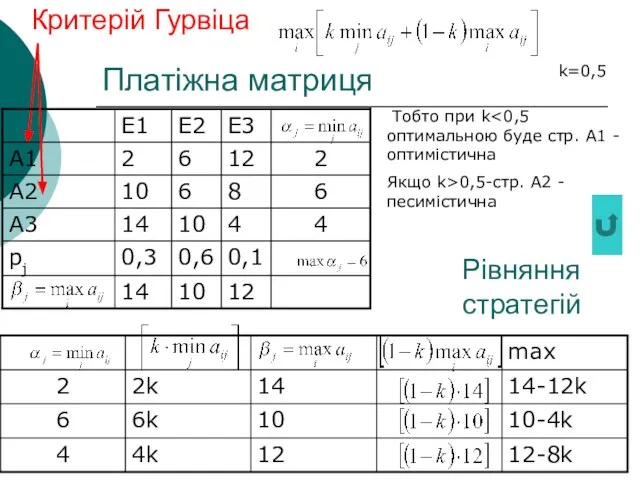
Платіжна матриця
Критерій Гурвіца
Рівняння
стратегій
Якщо k=0, то мах=14 (стратегія А1)
якщо k=1, то мах=6 (стратегія А2)
14-12k=10-4k; 8k=4; k=0,5
Умова оптимізму і найв.ризику
Умова песимізму і найм.ризику

Платіжна матриця
Критерій Гурвіца
Рівняння
стратегій
Тобто при k<0,5 оптимальною буде стр. А1 - оптимістична
Якщо k>0,5-стр. А2 - песимістична
k=0,5

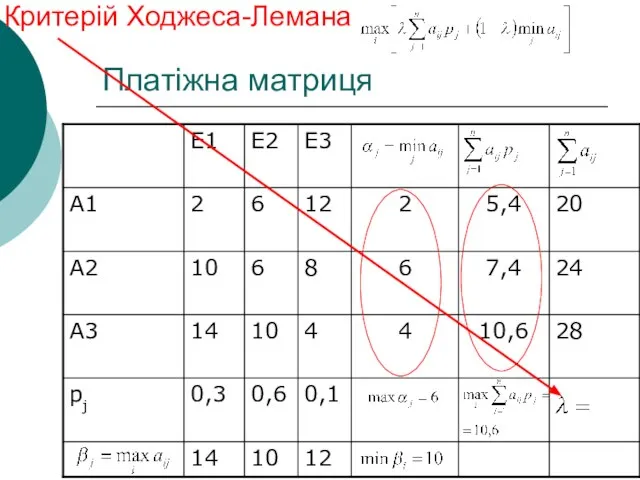
Платіжна матриця
Критерій Ходжеса-Лемана

Платіжна матриця
Критерій Ходжеса-Лемана
При оптимальною буде стратегія А2, а при - стратегія А3. Отже, за критерієм Ходжеса-Лемана оптимальними можуть бути дві стратегії

Таблиця коефіцієнтів оптимальності

ВИСНОВОК
Якщо критерії свідчать по те, що необхідно прийняти одне й те саме рішення, то це підтверджує його оптимальність. У випадку вказівки на різні рішення, пріоритет варто віддати тому з них, у якого більше математичне сподівання. У ситуації ризику він є основним

Приклад – аналіз комерційної стратегії при невизначеній кон”юнктурі
Компанія виробляє продукцію певного асортименту і здійснює її збут по чотирьох каналах:
Щомісячний обсяг продукції зі стійкими зв”язками по збуту на кілька років в середньому становить 490000 у.о.
Щомісячний обсяг продукції зі стійким збутом, але не на довгий термін – 500000 у.о.
Щомісячний обсяг продукції забезпечено тільки разовими закупівлями – 510000 у.о.
Місячна продукція, покупець на яку не визначений – 480000 у.о.
Компанія може здійснювати виробництво продукції за трьома проектами в обсягах 980000 у.о., 1500000 у.о. і 1980000 у.о.
Необхідно обрати оптимальну стратегію виробництва

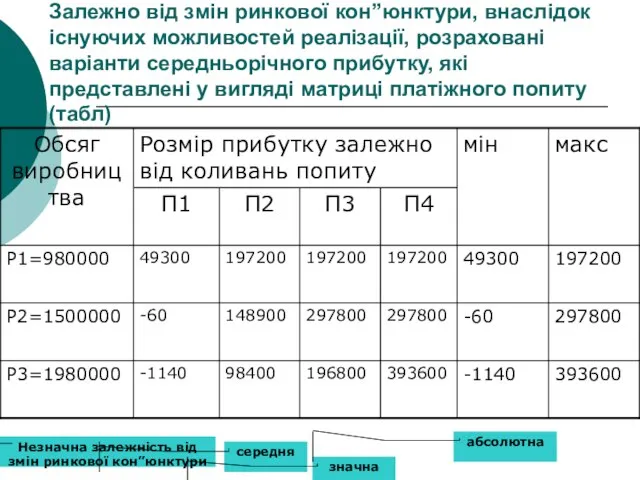
Залежно від змін ринкової кон”юнктури, внаслідок існуючих можливостей реалізації, розраховані варіанти середньорічного прибутку, які представлені у вигляді матриці платіжного попиту (табл)
Незначна залежність від змін ринкової кон”юнктури
середня
значна
абсолютна