Технология Data Mining

Data Mining
Это собирательное название, используемое для обозначения совокупности методов обнаружения в данных ранее неизвестных, нетривиальных, практически полезных и доступных интерпретации знаний, необходимых для принятия решений в различных сферах человеческой деятельности.
Определение. Data Mining - это процесс поддержки принятия решений, основанный на поиске в данных скрытых закономерностей (шаблонов информации).

Классификация задач Data Mining
классификация,
кластеризация,
прогнозирование,
ассоциация,
визуализация,
анализ и обнаружение отклонений,
оценивание,
анализ связей.

Основные методы Data mining
методы классификации, моделирования и прогнозирования, основанные на применении деревьев решений, искусственных нейронных сетей, генетических алгоритмов, эволюционного программирования, ассоциативной памяти, нечёткой логики;
статистические методы - дескриптивный анализ, корреляционный и регрессионный анализ, факторный анализ, дисперсионный анализ, компонентный анализ, дискриминантный анализ, анализ временных рядов.

Нечеткая логика
Математическая теория нечетких множеств (fuzzy sets) и нечеткая логика (fuzzy logic) являются обобщениями классической теории множеств и классической формальной логики.
Данные понятия были впервые предложены американским ученым Лотфи Заде (Lotfi Zadeh) в 1965 г.
Основной причиной появления новой теории стало наличие нечетких и приближенных рассуждений при описании человеком процессов, систем, объектов.

Периоды развития
Первый период (конец 60-х–начало 70 гг.) характеризуется развитием теоретического аппарата нечетких множеств (Л. Заде, Э. Мамдани, Беллман).
Во втором периоде (70–80-е годы) появляются первые практические результаты в области нечеткого управления сложными техническими системами (парогенератор с нечетким управлением).
Наконец, в третьем периоде, который длится с конца 80-х годов и продолжается в настоящее время, появляются пакеты программ для построения нечетких экспертных систем, а области применения нечеткой логики заметно расширяются.

Математический аппарат
Характеристикой нечеткого множества выступает функция принадлежности (Membership Function). Обозначим через MF(x) – степень принадлежности к нечеткому множеству C
Тогда нечетким множеством С называется множество упорядоченных пар вида C={MFc(x)/x}, MFc(x) [0,1]. Значение MFc(x)=0 означает отсутствие принадлежности к множеству, 1 – полную принадлежность.
Для нечетких множеств, как и для обычных, определены основные логические операции. Самыми основными, необходимыми для расчетов, являются пересечение и объединение.
Пересечение двух нечетких множеств (нечеткое "И"): A B: MFAB(x)=min(MFA(x), MFB(x)).
Объединение двух нечетких множеств (нечеткое "ИЛИ"): A B: MFAB(x)=max(MFA(x), MFB(x)).

Нечеткая и лингвистическая переменные
Нечеткая переменная описывается набором (N,X,A), где N – это название переменной, X – универсальное множество (область рассуждений), A – нечеткое множество на X.
Значениями лингвистической переменной (N,T,X,G,P) могут быть нечеткие переменные, т.е. лингвистическая переменная находится на более высоком уровне, чем нечеткая переменная.
Каждая лингвистическая переменная состоит из:
названия;
множества своих значений, которое также называется базовым терм-множеством T. Элементы базового терм-множества представляют собой названия нечетких переменных;
универсального множества X;
синтаксического правила G, по которому генерируются новые термы с применением слов естественного или формального языка;
семантического правила P, которое каждому значению лингвистической переменной ставит в соответствие нечеткое подмножество множества X.

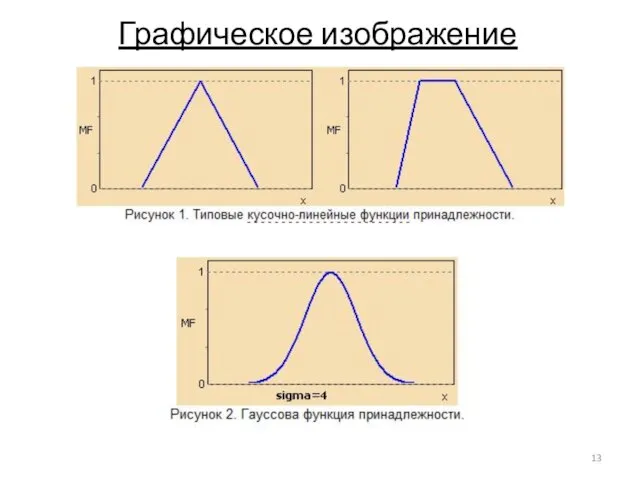
Типовые формы кривых для задания функций принадлежности
Существует свыше десятка типовых форм кривых для задания функций принадлежности. Наибольшее распространение получили:
треугольная,
трапецеидальная,
гауссова функции принадлежности.

Треугольная функция принадлежности
Определяется тройкой чисел (a,b,c), и ее значение в точке x вычисляется согласно выражению:

Трапецеидальная функция принадлежности
Для задания трапецеидальной функции принадлежности необходима четверка чисел (a,b,c,d):

Гауссова функция принадлежности
Функция принадлежности гауссова типа описывается формулой:
где с – центра нечеткого множества

Графическое изображение

Формализация неточного понятия «возраст человека»
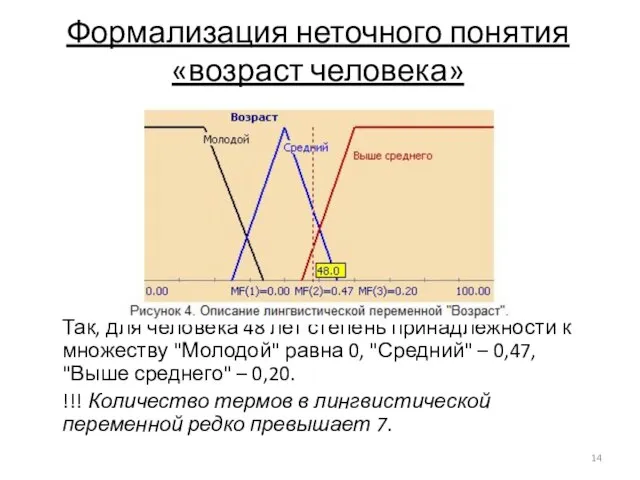
Так, для человека 48 лет степень принадлежности к множеству "Молодой" равна 0, "Средний" – 0,47, "Выше среднего" – 0,20.
!!! Количество термов в лингвистической переменной редко превышает 7.

Механизм логического вывода
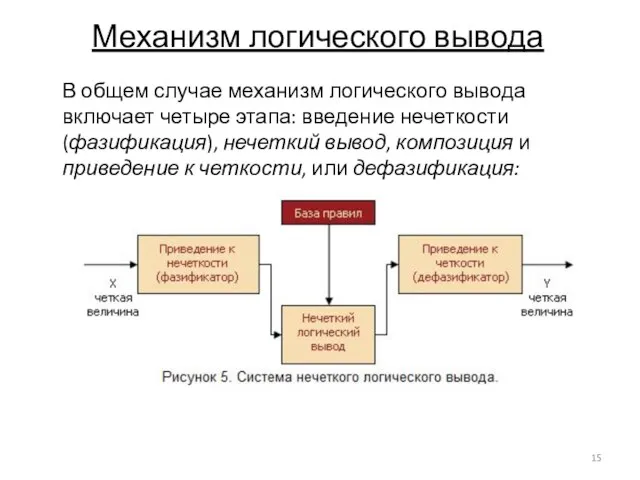
В общем случае механизм логического вывода включает четыре этапа: введение нечеткости (фазификация), нечеткий вывод, композиция и приведение к четкости, или дефазификация:

Интеграция с интеллектуальными парадигмами
Гибридизация методов интеллектуальной обработки информации – девиз, под которым прошли 90-е годы у западных и американских исследователей. В результате объединения нескольких технологий искусственного интеллекта появился специальный термин – "мягкие вычисления" (soft computing), который ввел Л. Заде в 1994 году.

Примеры объединения нескольких технологий
Нечеткие нейронные сети,
Адаптивные нечеткие системы,
Нечеткие запросы,
Нечеткие ассоциативные правила,
Нечеткие когнитивные карты,
Нечеткая кластеризация и т. п.

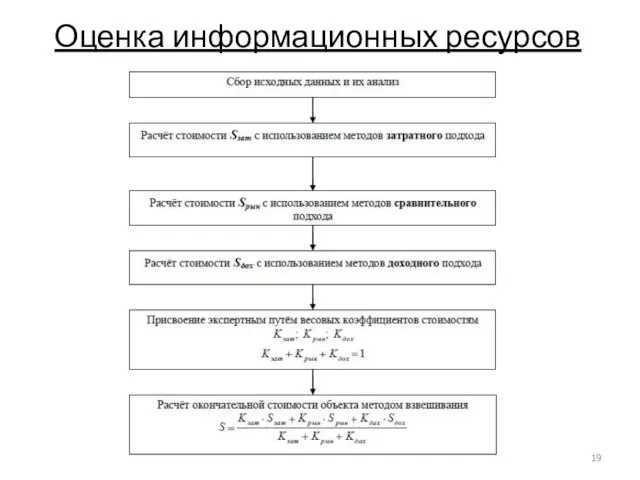
Применение методов нечеткой логики при оценке информационных ресурсов предприятий
Информационные ресурсы организации (ИР) – ресурсы нового типа, характеризующие интеллектуальный потенциал организации – до сих пор не рассматриваются руководителями и бухгалтерами как объекты финансового учѐта.
Большинство российских организаций на сегодняшний день не решают задач инвентаризации, оценки и коммерциализации информационных ресурсов, что противоречит современным методам управления.
Идентификация, анализ и оценка информационных ресурсов становится экономической необходимостью для любой организации независимо от еѐ размера и вида деятельности.

Оценка информационных ресурсов

Предположим, что стоимости, полученные тремя основными методами, представляют собой Т – числа и имеют следующие значения (в тыс. руб.):
Sзат=[100; 250; 450; 650];
Sрын=[400; 525; 650; 800];
Sдох=[450; 650; 725; 1000]. Схематическое представление данной оценки ИР в форме лингвистической переменной, включающей в себя три метода оценивания (затратный, рыночный и доходный), представлена на рисунке.

Нечеткая оценка стоимости ИР

Таблица 1

Таблица 2

Таблица 3

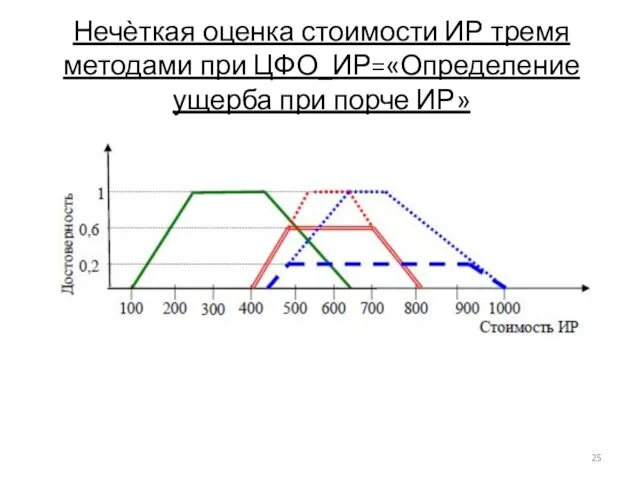
Нечѐткая оценка стоимости ИР тремя методами при ЦФО_ИР=«Определение ущерба при порче ИР»

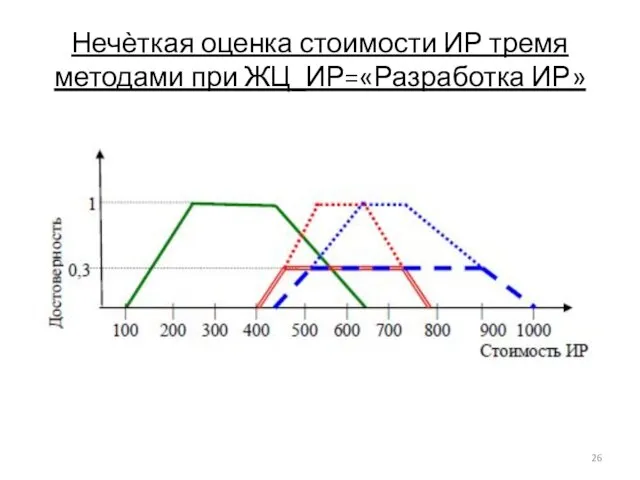
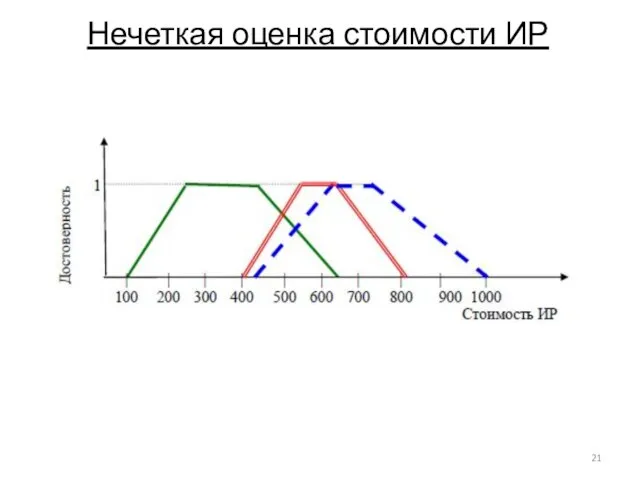
Нечѐткая оценка стоимости ИР тремя методами при ЖЦ_ИР=«Разработка ИР»

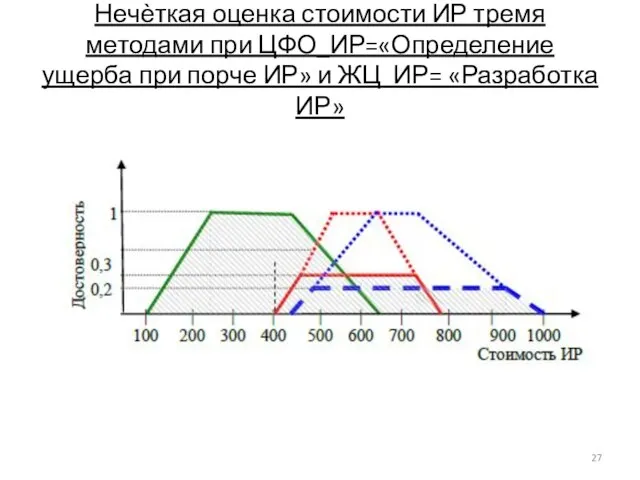
Нечѐткая оценка стоимости ИР тремя методами при ЦФО_ИР=«Определение ущерба при порче ИР» и ЖЦ_ИР= «Разработка ИР»

Результат
На основе полученной нечѐткой оценки стоимости ИР путѐм дефаззификации определяется чѐткая оценка ИР, равная абсциссе центра тяжести заштрихованной фигуры