Содержание
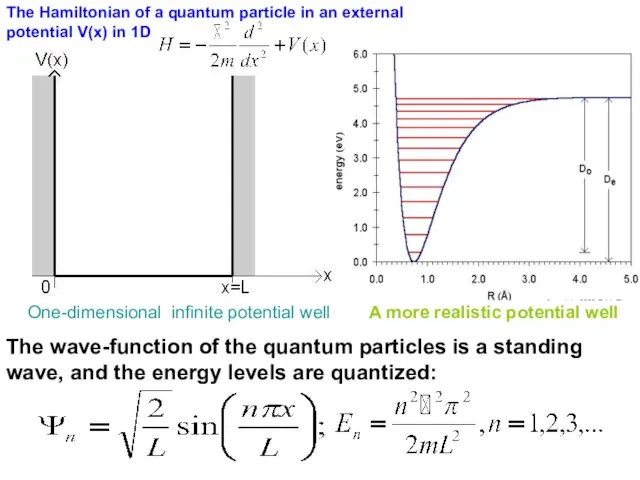
- 7. One-dimensional infinite potential well The wave-function of the quantum particles is a standing wave, and the
- 8. Статистика энергетических уровней тяжелых ядер Вигнер, Дайсон, Мета, Година (Gaudin) (1960-65) и изолировнных металлических гранул (Горьков,
- 9. Вигнер и Дайсон исследовали ансамбль из случайных эрмитовых матриц размерности распределенных по закону: где с –
- 10. Важный вопрос: возможно ли отделить распределение N уровней энергии Ei от распределения остальных (NxN – N)
- 11. Следовательно, для перехода к распределению по энергетическим уровням от распределения по матричным элементам необходим якобиан перехода
- 12. The Wigner’s Ansatz for the Gaussian ensemble of random NxN Hermitian matrices H : In the
- 13. Step 3 Step 4 Step 5 where levels distribution function is: Equivalent form for the distribution
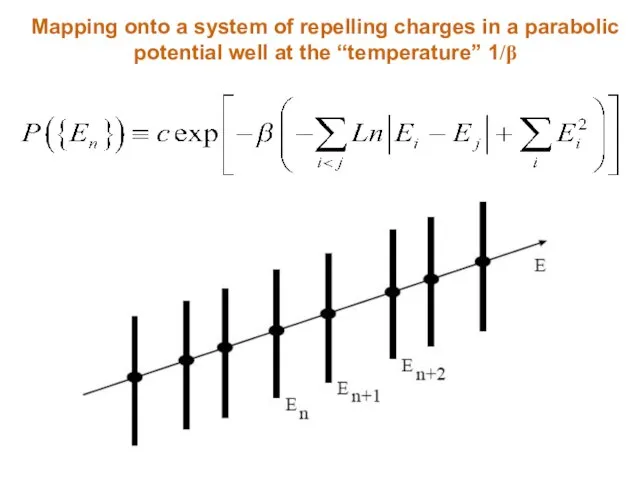
- 14. Mapping onto a system of repelling charges in a parabolic potential well at the “temperature” 1/β
- 17. β=1 (!)
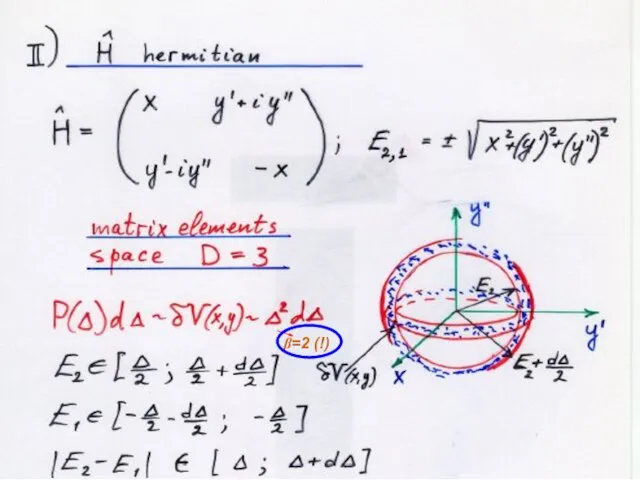
- 18. β=2 (!)
- 19. β=4 (!)
- 21. The problem: how the GOE to GUE crossover looks like when an external magnetic field is
- 22. A real NxN antisymmetric matrix A is independently distributed from real symmetric matrix H0 . Both
- 23. Двухуровневая корреляционная функция во внешнем магнитном поле: аналитическое решение Pandey&Mehta (1991) ; баллистическое движение
- 24. диффузия R>>l l – длина своб.пробега R-размер образца; vf-скорость Ферми; δ − среднее межуровневое расстояние Fram&Pichard
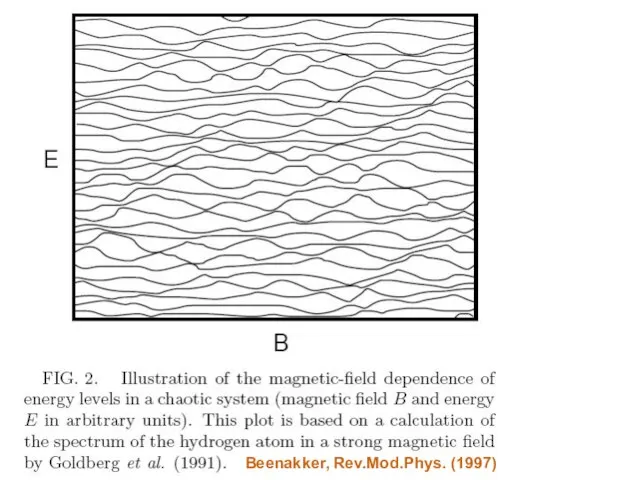
- 25. Beenakker, Rev.Mod.Phys. (1997)
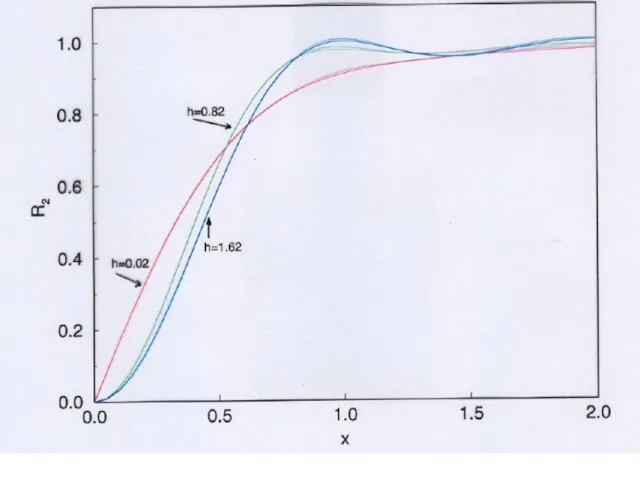
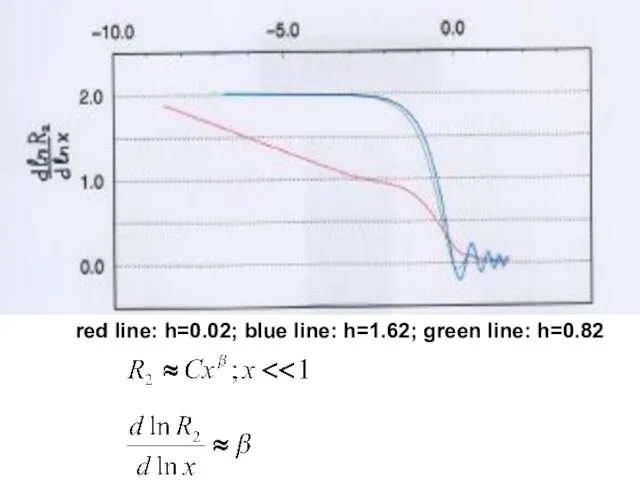
- 27. red line: h=0.02; blue line: h=1.62; green line: h=0.82
- 29. Скачать презентацию
















 КОВАЛЕВ АЛЕКСАНДР ПЕТРОВИЧ директор ФГУ «ДальНИИЛХ», д.с-х.н, профессор
КОВАЛЕВ АЛЕКСАНДР ПЕТРОВИЧ директор ФГУ «ДальНИИЛХ», д.с-х.н, профессор Реализация инвестиционного проекта Группы «Илим» в Иркутской области и предложения по повышению эффективности использования ле
Реализация инвестиционного проекта Группы «Илим» в Иркутской области и предложения по повышению эффективности использования ле Презентация на тему Приветствие в разных странах
Презентация на тему Приветствие в разных странах Ноу-хау как объект интеллектульной собственности
Ноу-хау как объект интеллектульной собственности Куда пойти после уроков. Кружки и секции города
Куда пойти после уроков. Кружки и секции города «Применение лечебно- профилактического танца для детей дошкольного возраста»Составитель: инструктор по физической культуре Л
«Применение лечебно- профилактического танца для детей дошкольного возраста»Составитель: инструктор по физической культуре Л Презентация "Архитектура неоклассицизма XVIII в" - скачать презентации по МХК
Презентация "Архитектура неоклассицизма XVIII в" - скачать презентации по МХК ОБЕЗБОЛИВАНИЯ СКЭНАРОМ ПРИ БОЛЯХ В СПИНЕ НА ДОГОСПИТАЛЬНОМ ЭТАПЕ МУЛЬТИЦЕНТРОВОЕ СРАВНИТЕЛЬНОЕ ИССЛЕДОВАНИЕBACK PAIN AND SCENAR - PREHOSPITA
ОБЕЗБОЛИВАНИЯ СКЭНАРОМ ПРИ БОЛЯХ В СПИНЕ НА ДОГОСПИТАЛЬНОМ ЭТАПЕ МУЛЬТИЦЕНТРОВОЕ СРАВНИТЕЛЬНОЕ ИССЛЕДОВАНИЕBACK PAIN AND SCENAR - PREHOSPITA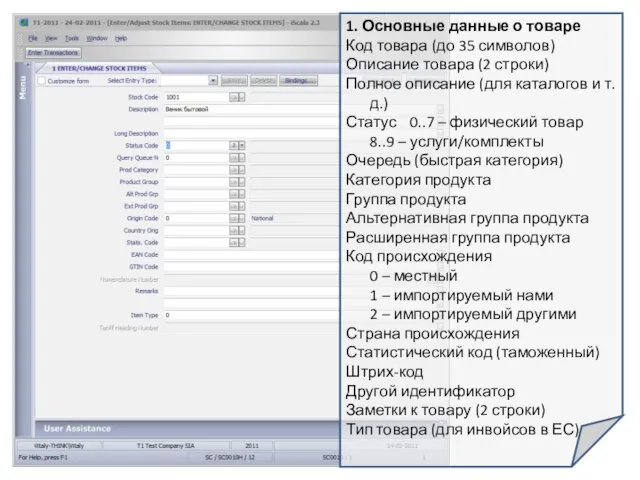 1. Основные данные о товаре Код товара (до 35 символов) Описание товара (2 строки) Полное описание (для каталогов и т.д.) Статус 0..7 – физ
1. Основные данные о товаре Код товара (до 35 символов) Описание товара (2 строки) Полное описание (для каталогов и т.д.) Статус 0..7 – физ Связи с общественностью как инструмент корпоративной социальной ответственности
Связи с общественностью как инструмент корпоративной социальной ответственности Муниципальное общеобразовательное учреждениесредняя общеобразовательная школа №21Первомайского района г. Ростова-на-ДонуБибл
Муниципальное общеобразовательное учреждениесредняя общеобразовательная школа №21Первомайского района г. Ростова-на-ДонуБибл Работа с папками и файлами с помощью меню и панели инструментов проводника
Работа с папками и файлами с помощью меню и панели инструментов проводника Давление газов
Давление газов Учетная норма площади жилья по договору социального найма
Учетная норма площади жилья по договору социального найма Санитарно-техническое устройство парикмахерской
Санитарно-техническое устройство парикмахерской Параллельность прямых
Параллельность прямых Классификация чугунов
Классификация чугунов Декодирование информации (3 класс)
Декодирование информации (3 класс)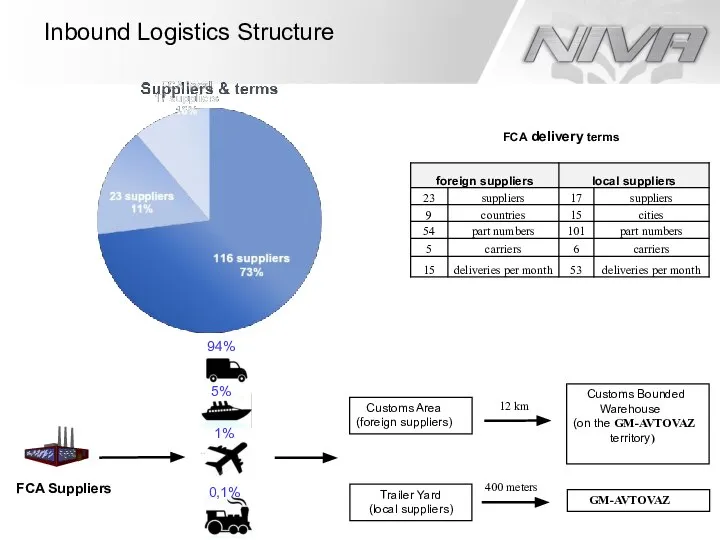 Inbound Logistics Structure Suppliers & terms
Inbound Logistics Structure Suppliers & terms Ценообразование
Ценообразование  Пути развития современной архитектуры и дизайна
Пути развития современной архитектуры и дизайна Финансовая математика
Финансовая математика Мобільність IP- телефоні
Мобільність IP- телефоні Знакомство с электронными таблицами MICROSOFT EXCEL
Знакомство с электронными таблицами MICROSOFT EXCEL Изменения в законодательстве, вступающие в силу в период с 01 октября по 31 декабря 2019 года
Изменения в законодательстве, вступающие в силу в период с 01 октября по 31 декабря 2019 года Множественное число существительных
Множественное число существительных А.С. Пушкин Повесть «Капитанская дочка»
А.С. Пушкин Повесть «Капитанская дочка» ТОРГОВЫЕ АВТОМАТЫ
ТОРГОВЫЕ АВТОМАТЫ