Презентация на тему Как все двигается с точки зрения физики

Квантовая физика. Фотоэффект
Фотоэлектрический эффект был открыт в 1887 году немецким физиком Г. Герцем и в 1888–1890 годах экспериментально исследован А. Г. Столетовым. Наиболее полное исследование явления фотоэффекта было выполнено Ф. Ленардом в 1900 г. К этому времени уже был открыт электрон (1897 г., Дж. Томсон), и стало ясно, что фотоэффект (или точнее – внешний фотоэффект) состоит в вырывании электронов из вещества под действием падающего на него света.

Посмотрим, какие закономерности мы предскажем, находясь в рамках классической физики (конец 19-го века – начало 20-го).
Электроны должны быть связаны в твердом теле, иначе сколь угодно малое электрическое поле приводило бы к их эмиссии. Поэтому для выхода электронов надо сообщить им дополнительную энергию.
При фотоэффекте энергия приобретается за счет электромагнитного поля. Пусть E = E0cos(ωt) – напряженность электрического поля в электромагнитной волне. Это поле воздействует на электрон, сообщая ему кинетическую энергию Te.
Теория показывает, что кинетическая энергия электрона Te зависит от параметров падающей волны как Te ~ E02/ω2. Если эта энергия больше работы выхода А из металла (Te > А) ,электрон может покинуть образец.
Сразу же напрашиваются по крайней мере три вывода о свойствах явления:
Чем выше интенсивность световой волны I0=E02 ,тем больше энергия электронов Te.
Вырывание электронов носит пороговый характер по напряженности поля E0 , то есть условие Te > А не может быть выполнено при малых E0.
При постоянной интенсивности I0 =E02 увеличение частоты падающей волны ω снижает энергию выбиваемых электронов Te.

В экспериментах использовался стеклянный вакуумный баллон с двумя металлическими электродами, поверхность которых была тщательно очищена. К электродам прикладывалось некоторое напряжение U, полярность которого можно было изменять с помощью двойного ключа. Один из электродов (катод K) через кварцевое окошко освещался монохроматическим светом некоторой длины волны λ. При неизменном световом потоке снималась зависимость силы фототока I от приложенного напряжения (вольтамперная характеристика).
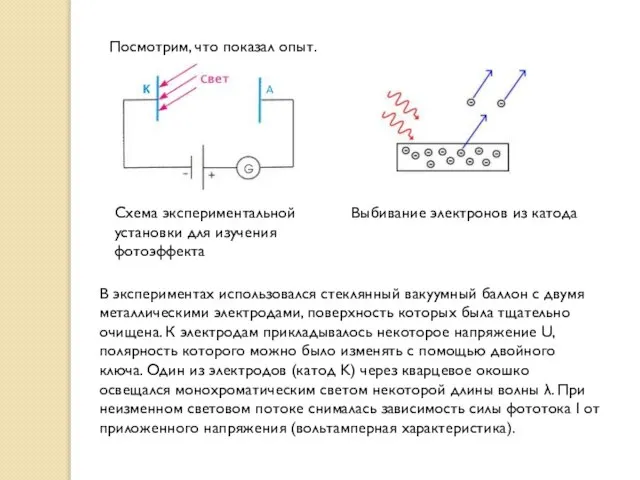
Схема экспериментальной установки для изучения фотоэффекта
Посмотрим, что показал опыт.
Выбивание электронов из катода

Зависимость силы фототока от приложенного напряжения (вольтамперная характеристика) фотоэффекта. Кривая 2 соответствует большей интенсивности светового потока. Iн1 и Iн2 – токи насыщения, Uз – запирающий потенциал
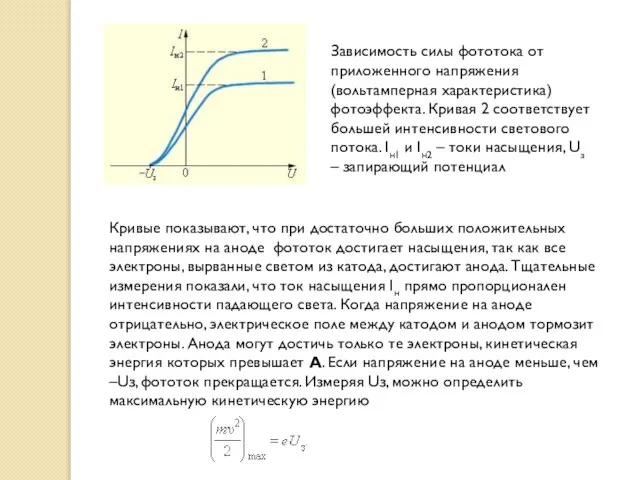
Кривые показывают, что при достаточно больших положительных напряжениях на аноде фототок достигает насыщения, так как все электроны, вырванные светом из катода, достигают анода. Тщательные измерения показали, что ток насыщения Iн прямо пропорционален интенсивности падающего света. Когда напряжение на аноде отрицательно, электрическое поле между катодом и анодом тормозит электроны. Анода могут достичь только те электроны, кинетическая энергия которых превышает А. Если напряжение на аноде меньше, чем –Uз, фототок прекращается. Измеряя Uз, можно определить максимальную кинетическую энергию

Зависимость запирающего потенциала Uз (максимальной кинетической энергии электронов) от частоты падающего света
Многочисленными экспериментаторами были установлены следующие основные закономерности фотоэффекта:
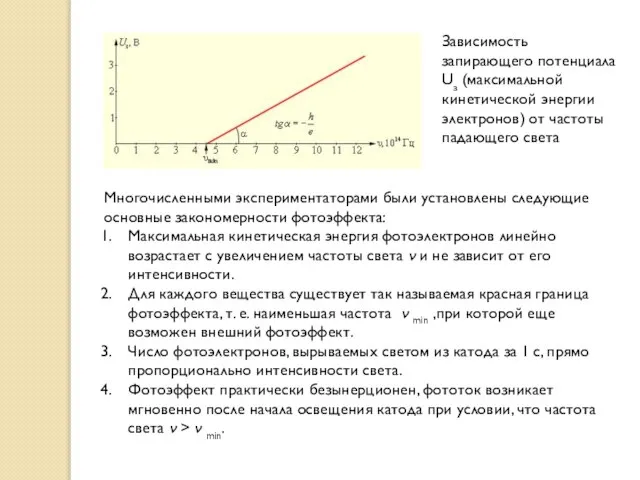
Максимальная кинетическая энергия фотоэлектронов линейно возрастает с увеличением частоты света ν и не зависит от его интенсивности.
Для каждого вещества существует так называемая красная граница фотоэффекта, т. е. наименьшая частота ν min ,при которой еще возможен внешний фотоэффект.
Число фотоэлектронов, вырываемых светом из катода за 1 с, прямо пропорционально интенсивности света.
Фотоэффект практически безынерционен, фототок возникает мгновенно после начала освещения катода при условии, что частота света ν > ν min.

Все эти закономерности фотоэффекта в корне противоречили представлениям классической физики о взаимодействии света с веществом.
Согласно волновым представлениям при взаимодействии с электромагнитной световой волной электрон должен был бы постепенно накапливать энергию, и потребовалось бы значительное время, зависящее от интенсивности света, чтобы электрон накопил достаточно энергии для того, чтобы вылететь из катода. Как показывают расчеты, это время должно было бы исчисляться минутами или часами. Однако, опыт показывает, что фотоэлектроны появляются немедленно после начала освещения катода.
В этой модели также было невозможно понять существование красной границы фотоэффекта. Волновая теория света не могла объяснить независимость энергии фотоэлектронов от интенсивности светового потока и пропорциональность максимальной кинетической энергии частоте света.
Таким образом, электромагнитная теория света оказалась неспособной объяснить эти закономерности.

Выход был найден А. Эйнштейном в 1905 г. Теоретическое объяснение было дано на основе гипотезы М. Планка о том, что свет излучается и поглощается определенными порциями, причем энергия каждой такой порции определяется формулой
E = hν,
где h – постоянная Планка.
Эйнштейн сделал следующий шаг в развитии квантовых представлений. Он пришел к выводу, что свет имеет прерывистую (дискретную) структуру. Электромагнитная волна состоит из отдельных порций – квантов, впоследствии названных фотонами. При взаимодействии с веществом фотон целиком передает всю свою энергию hν одному электрону. Часть энергии электрона затрачивается на преодоление потенциального барьера на границе металл–вакуум. Для этого электрон должен совершить работу выхода A, зависящую от свойств материала катода. Наибольшая кинетическая энергия, которую может иметь вылетевший из катода фотоэлектрон, определяется законом сохранения энергии (уравнение Эйнштейна для фотоэффекта):

С помощью уравнения Эйнштейна можно объяснить все закономерности внешнего фотоэффекта.
Из уравнения Эйнштейна следуют
линейная зависимость максимальной кинетической энергии от частоты и независимость от интенсивности света
существование красной границы
безынерционность фотоэффекта
Общее число фотоэлектронов, покидающих за 1 с поверхность катода, должно быть пропорционально числу фотонов, падающих за то же время на поверхность. Из этого следует, что ток насыщения должен быть прямо пропорционален интенсивности светового потока.
Как следует из уравнения Эйнштейна, тангенс угла наклона прямой, выражающей зависимость запирающего потенциала Uз от частоты ν, равен отношению постоянной Планка h к заряду электрона e:

Это позволяет экспериментально определить значение постоянной Планка. Такие измерения были выполнены в 1914 г. Р. Милликеном и дали хорошее согласие со значением, найденным Планком. Эти измерения позволили также определить работу выхода A:
где c – скорость света, λкр – длина волны, соответствующая красной границе фотоэффекта. У большинства металлов работа выхода A составляет несколько электрон-вольт (1 эВ = 1,602·10–19 Дж).
Наименьшей работой выхода обладают щелочные элементы. Например, у натрия A = 1,9 эВ, что соответствует красной границе фотоэффекта λкр ≈ 680 нм. Поэтому соединения щелочных металлов используют для создания катодов в фотоэлементах, предназначенных для регистрации видимого света.

В решении Комитета о присуждении Нобелевской премии А.Эйнштейну в 1921 году записано:
ALBERT EINSTEIN for his services to Theoretical Physics, and especially for his discovery of the law of the photoelectric effect.
("за его вклад в теоретическую физику и, особенно, за его открытие закона фотоэффекта").
Зависимость задерживающего напряжения от частоты излучения, как мы видели, имеет вид прямой линии, наклон которой определяется значением постоянной Планка.
Измерив этот наклон экспериментально для натрия, магния, меди и алюминия, Р.Милликен в 1914 г. с хорошей точностью вычислил значение постоянной Планка.
Нобелевская премия присуждена Милликену в 1923г.:
ROBERT ANDREWS MILLIKAN for his work on the elementary charge of electricity and on the photoelectric effect.
("за его работы по элементарному электрическому заряду и фотоэлектрическому эффекту")

Итак, законы фотоэффекта свидетельствуют, что свет при испускании и поглощении ведет себя подобно потоку частиц, получивших название фотонов или световых квантов.
Таким образом, учение о свете, совершив виток длительностью в два столетия, вновь возвратилось к представлениям о световых частицах – корпускулах.
Но это не был механический возврат к корпускулярной теории Ньютона. В начале XX века стало ясно, что свет обладает двойственной природой. При распространении света проявляются его волновые свойства (интерференция, дифракция, поляризация), а при взаимодействии с веществом – корпускулярные (фотоэффект). Эта двойственная природа света получила название корпускулярно-волнового дуализма.
Позже двойственная природа была открыта у электронов и других элементарных частиц. Классическая физика не может дать наглядной модели сочетания волновых и корпускулярных свойств у микрообъектов. Движением микрообъектов управляют не законы классической механики Ньютона, а законы квантовой физики.

Образование — это то, что остается после того, когда забываешь все, чему учили в школе.
Ценность человека должна определяться тем, что он дает, а не тем, чего он способен добиться. Старайтесь стать не успешным, а ценным человеком.
Воображение важнее знания. Знание ограничено. Воображение охватывает весь мир.
Бесконечны лишь Вселенная и глупость человеческая. Хотя насчет первой у меня имеются сомнения.
А.Эйнштейн

Квантовая физика. Тепловое излучение тел
Испускаемый источником свет уносит с собой энергию. Существует много различных механизмов подвода энергии к источнику света. В тех случаях, когда необходимая энергия сообщается нагреванием, т. е. подводом тепла, излучение называется тепловым или температурным. Этот вид излучения для физиков конца XIX века представлял особый интерес, так как в отличие от всех других видов люминесценции, тепловое излучение может находиться в состоянии термодинамического равновесия с нагретыми телами.
Изучая закономерности теплового излучения тел, физики надеялись установить взаимосвязь между термодинамикой и оптикой.
Если в замкнутую полость с зеркально отражающими стенками поместить несколько тел, нагретых до различной температуры, то, как показывает опыт, такая система с течением времени приходит в состояние теплового равновесия, при котором все тела приобретают одинаковую температуру.

Пусть одно из тел в полости обладает свойством поглощать всю падающую на его поверхность лучистую энергию любого спектрального состава. Такое тело называют абсолютно черным.
Задача сводится к изучению спектрального состава излучения абсолютно черного тела. Решить эту задачу классическая физика оказалась не в состоянии.
Для установления равновесия в полости необходимо, чтобы каждое тело испускало ровно столько лучистой энергии, сколько оно поглощает. Это одна из важнейших закономерностей теплового излучения. Отсюда следует, что при заданной температуре абсолютно черное тело испускает с поверхности единичной площади в единицу времени больше лучистой энергии, чем любое другое тело.
Абсолютно черных тел в природе не бывает.
Хорошей моделью такого тела является небольшое отверстие в замкнутой полости

Физики шутят…
Абсолютно черное тело

Тела обмениваются энергией только путем испускания и поглощения лучистой энергии. В состоянии равновесия процессы испускания и поглощения энергии каждым телом в среднем компенсируют друг друга, и в пространстве между телами плотность энергии излучения достигает определенного значения, зависящего только от установившейся температуры тел.
Это излучение, находящееся в термодинамическом равновесии с телами, имеющими определенную температуру, называется равновесным или черным излучением. Плотность энергии равновесного излучения и его спектральный состав зависят только от температуры.
Если через малое отверстие заглянуть внутрь полости, в которой установилось термодинамическое равновесие между излучением и нагретыми телами, то глаз не различит очертаний тел и зафиксирует лишь однородное свечение всей полости в целом.

С увеличением температуры внутри полости будет возрастать энергия выходящего из отверстия излучения и изменяться его спектральный состав.
Распределение энергии по длинам волн в излучении абсолютно черного тела при заданной температуре T характеризуется излучательной способностью r (λ, T), равной мощности излучения с единицы поверхности тела в единичном интервале длин волн. Произведение r (λ, T) Δ λ равно мощности излучения, испускаемого единичной площадкой поверхности по всем направлениям в интервале Δ λ длин волн. Аналогично можно ввести распределение энергии по частотам r ( ν, T). Функцию r (ν, T) (или r (λ, T)) часто называют спектральной светимостью, а полный поток R (T) излучения всех длин волн, равный
называют интегральной светимостью тела.

К концу XIX века излучение абсолютно черного тела было хорошо изучено экспериментально.
В 1879 году Йозеф Стефан на основе анализа экспериментальных данных пришел к заключению, что интегральная энергетическая светимость R (T) абсолютно черного тела пропорциональна четвертой степени абсолютной температуры T:
R (T) = σT4
Несколько позднее, в 1884 году, Людвиг Больцман вывел эту зависимость теоретически, исходя из термодинамических соображений. Этот закон получил название закона Стефана–Больцмана.
К концу 90-х годов XIX века были выполнены тщательные экспериментальные измерения спектрального распределения излучения абсолютно черного тела, которые показали, что при каждом значении температуры T зависимость r (λ, T) имеет ярко выраженный максимум.

Спектральное распределение r (λ, T) излучения черного тела при различных температурах
С увеличением температуры максимум смещается в область коротких длин волн, причем произведение температуры T на длину волны λm ,соответствующую максимуму, остается постоянным:
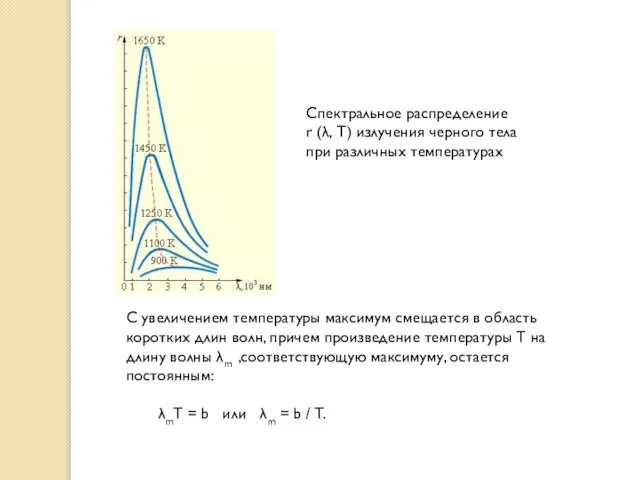
λmT = b или λm = b / T.

Это соотношение ранее было получено Вильгельм Вином из термодинамики. Оно выражает так называемый закон смещения Вина: длина волны λm ,на которую приходится максимум энергии излучения абсолютно черного тела, обратно пропорциональна абсолютной температуре T.
При практически достижимых в лабораторных условиях температурах максимум излучательной способности r (λ, T) лежит в инфракрасной области.
Только при T ≥ 5·103 К максимум попадает в видимую область спектра. Максимум энергии излучения Солнца приходится примерно на 470 нм (зеленая область спектра), что соответствует температуре наружных слоев Солнца около 6200 К (если рассматривать Солнце как абсолютно черное тело).

Задача 1. Абсолютно черное тело нагрето от температуры 100 до 3000 С. Во сколько раз изменилась мощность суммарного излучения при этом.
Дано: Т1=1000С = 373К;
Т2=3000С = 573К;
σ=5,67 10-3 Вт /м2К 4.
Решение: Мощность излучения тела определяется выражением N=RS, где R-энергетическая светимость тела, S- площадь его поверхности. По закону Стефана-Больцмана R = σ Т4 . Из этих выражений получаем N2/N1= (σ Т24 S ) / (σ Т14 S )= (Т2 / Т1)4 = 5,6
Задача 2. Абсолютно черное тело имеет температуру 3000К. При остывании тела длина волны, соответствующая максимуму спектральной плотности энергетической светимости, изменилась на 8 мкм. Определить температуру, до которой охладилось тело.
Дано: Т1=3000К;
Δλ max=8 мкм=8 10-6 м;
b =2,89 10-3 м К.
В соответствии с законом Вина Δλ max = λ 1 max − λ 2 max = b/T2 - b/T1
Отсюда T2 = bT1/(b+ T1Δλ max) = 323 К.

Успехи термодинамики, позволившие вывести законы Стефана–Больцмана и Вина теоретически, вселяли надежду, что, исходя из термодинамических соображений, удастся получить всю кривую спектрального распределения излучения черного тела r(λ, T). В 1900 году эту проблему пытался решить знаменитый английский физик лорд Д. Релей, который в основу своих рассуждений положил теорему классической статистической механики о равномерном распределении энергии по степеням свободы в состоянии термодинамического равновесия. Эта теорема была применена Релеем к равновесному излучению в полости. Несколько позже эту идею подробно развил Д. Джинс. Таким путем удалось получить зависимость излучательной способности абсолютно черного тела от длины волны λ и температуры T:
r (λ, T) = 8πkT / λ4.

Это соотношение называют формулой Релея–Джинса. Оно согласуется с экспериментальными данными только в области достаточно длинных волн . Кроме того, из нее следует абсурдный вывод о том, что интегральная светимость R (T) черного тела должна обращаться в бесконечность, а, следовательно, равновесие между нагретым телом и излучением в замкнутой полости может установиться только при абсолютном нуле температуры.
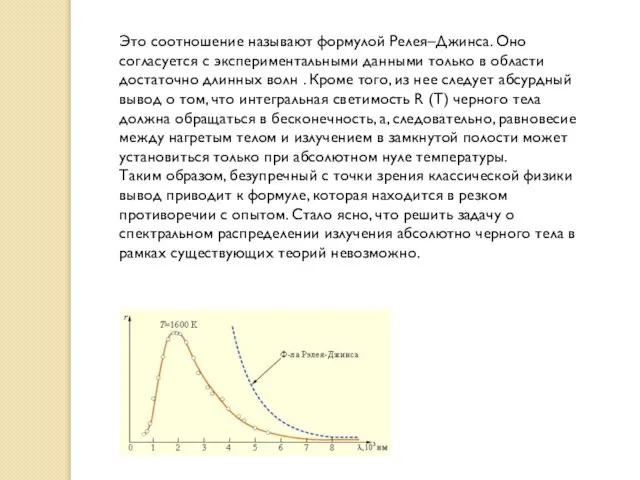
Таким образом, безупречный с точки зрения классической физики вывод приводит к формуле, которая находится в резком противоречии с опытом. Стало ясно, что решить задачу о спектральном распределении излучения абсолютно черного тела в рамках существующих теорий невозможно.

Эта задача была успешно решена М.Планком на основе новой идеи, чуждой классической физике.
Планк пришел к выводу, что процессы излучения и поглощения электромагнитной энергии нагретым телом происходят не непрерывно, как это принимала классическая физика, а конечными порциями – квантами. Квант – это минимальная порция энергии, излучаемой или поглощаемой телом. По теории Планка, энергия кванта E прямо пропорциональна частоте света:
E = hν
На основе гипотезы о прерывистом характере процессов излучения и поглощения телами электромагнитного излучения Планк получил формулу для спектральной светимости абсолютно черного тела. Формулу Планка обычно записывают в форме, выражающей распределение энергии в спектре излучения абсолютно черного тела по частотам ν, а не по длинам волн
где c – скорость света, h – постоянная Планка, k – постоянная Больцмана, T – абсолютная температура.

Квантовая физика. Эффект Комптона
Концепция фотонов, предложенная А. Эйнштейном в 1905 г. для объяснения фотоэффекта, в 1922 г. получила экспериментальное подтверждение в опытах американского физика А. Комптона.
Комптон исследовал упругое рассеяние коротковолнового рентгеновского излучения на свободных (или слабо связанных с атомами) электронах вещества. Открытый им эффект увеличения длины волны рассеянного излучения, названный впоследствии эффектом Комптона, не укладывается в рамки волновой теории, согласно которой длина волны излучения не должна изменяться при рассеянии. Согласно волновой теории, электрон под действием периодического поля световой волны совершает вынужденные колебания на частоте волны и поэтому излучает рассеянные волны той же частоты

Схема Комптона представлена на рис. Монохроматическое рентгеновское излучение с длиной волны λ0 , исходящее из рентгеновской трубки R, проходит через свинцовые диафрагмы и в виде узкого пучка направляется на рассеивающее вещество-мишень P (графит, алюминий). Излучение, рассеянное под некоторым углом θ, анализируется с помощью спектрографа рентгеновских лучей S, в котором роль дифракционной решетки играет кристалл K, закрепленный на поворотном столике. Опыт показал, что в рассеянном излучении наблюдается увеличение длины волны Δλ, зависящее от угла рассеяния θ:
где Λ = 2,43·10–3 нм – так называемая комптоновская длина волны, не зависящая от свойств рассеивающего вещества.

Спектры рассеянного излучения в опытах А.Комптона
Объяснение эффекта Комптона на основе квантовых представлений о природе излучения было дано в 1923 году независимо друг от друга А.Комптоном и П. Дебаем. Если принять, что излучение представляет собой поток фотонов, то эффект Комптона есть результат упругого столкновения рентгеновских фотонов со свободными электронами вещества. У легких атомов рассеивающих веществ электроны слабо связаны с ядрами атомов, поэтому их можно считать свободными. В процессе столкновения фотон передает электрону часть своей энергии и импульса в соответствии с законами сохранения.

Теоретический расчет, выполненный на основе квантовых представлений, дал исчерпывающее объяснение эффекту Комптона и позволил выразить комптоновскую длину волны Λ через фундаментальные константы h, c и m:
Поймал Мефистофель философа, инженера и физика-теоретика , и сказал: прыгайте с десятиметровой вышки в бассейн диаметром 1 метр.
Философ порассуждал, примерился, помедитировал, потом махнул рукой, авось повезет и прыгнул. Не повезло.
Инженер поднял палец, померил скорость ветра, просчитал несколько вариантов, прыгнул и попал точно в середину бассейна.
Физик-теоретик построил модель, написал программу, вычислил траекторию полета, построил график разбега. Разбежался, прыгнул и ... стрелой унесся вверх!!!
Ошибка в вычислениях, противоположный знак результата!
Физики шутят…

Квантовая физика. Волновые свойства микрочастиц. Дифракция электронов
В 1924 году произошло примечательное событие, которое в значительной степени ускорило развитие квантовой физики. Французский физик Л. де Бройль выдвинул гипотезу об универсальности корпускулярно-волнового дуализма. Де Бройль утверждал, что не только фотоны, но и электроны и любые другие частицы материи наряду с корпускулярными обладают также и волновыми свойствами.
Согласно де Бройлю, с каждым микрообъектом связаны, с одной стороны, корпускулярные характеристики – энергия E и импульс p, а с другой стороны, волновые характеристики – частота ν и длина волны λ.
Корпускулярные и волновые характеристики микрообъектов связаны такими же количественными соотношениями, как и у фотона:

Гипотеза де Бройля постулировала эти соотношения для всех микрочастиц, в том числе и для таких, которые обладают массой m. Любой частице, обладающей импульсом, сопоставлялся волновой процесс с длиной волны λ = h / p («длина волны де Бройля»). Для частиц, имеющих массу ,в нерелятивистском приближении (υ << c)
Гипотеза де Бройля основывалась на соображениях симметрии свойств материи и не имела в то время опытного подтверждения. Но она явилась мощным революционным толчком к развитию новых представлений о природе материальных объектов. В течение нескольких лет целый ряд выдающихся физиков XX века – В. Гейзенберг, Э. Шредингер, П. Дирак, Н. Бор и другие – разработали теоретические основы новой науки, которая была названа квантовой механикой.
П. Дирак

Первое экспериментальное подтверждение гипотезы де Бройля было получено в 1927 году американскими физиками К. Девиссоном и Л. Джермером.
Они обнаружили, что пучок электронов, рассеивающийся на кристалле никеля, дает отчетливую дифракционную картину, подобную той, которая возникает при рассеянии на кристалле коротковолнового рентгеновского излучения. В этих экспериментах кристалл играл роль естественной дифракционной решетки.
По положению дифракционных максимумов была определена длина волны электронного пучка, которая оказалась в полном соответствии с вычисленной по формуле де Бройля.

В следующем 1928 году английский физик Г. Томсон (сын Дж. Томсона, открывшего за 30 лет до этого электрон) получил новое подтверждение гипотезы де Бройля. В своих экспериментах Г. Томсон наблюдал дифракционную картину, возникающую при прохождении пучка электронов через тонкую поликристаллическую фольгу из золота.
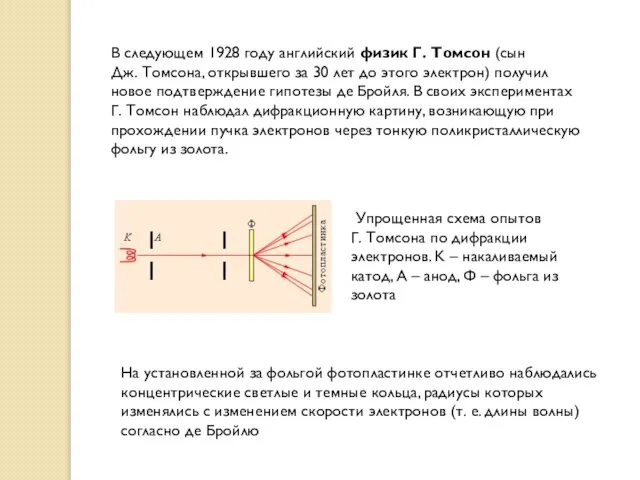
Упрощенная схема опытов Г. Томсона по дифракции электронов. K – накаливаемый катод, A – анод, Ф – фольга из золота
На установленной за фольгой фотопластинке отчетливо наблюдались концентрические светлые и темные кольца, радиусы которых изменялись с изменением скорости электронов (т. е. длины волны) согласно де Бройлю

Картина дифракции электронов на поликристаллическом образце при длительной экспозиции (a) и при короткой экспозиции (b). В случае (b) видны точки попадания отдельных электронов на фотопластинку.
В последующие годы опыт Дж. Томсона был многократно повторен с неизменным результатом, в том числе при условиях, когда поток электронов был настолько слабым, что через прибор единовременно могла проходить только одна частица (В. А. Фабрикант, 1948 г.). Таким образом, было экспериментально доказано, что волновые свойства присущи не только большой совокупности электронов, но и каждому электрону в отдельности.

Впоследствии дифракционные явления были обнаружены также для нейтронов, протонов, атомных и молекулярных пучков. Экспериментальное доказательство наличия волновых свойств микрочастиц привело к выводу о том, что это универсальное явление природы, общее свойство материи. Следовательно, волновые свойства должны быть присущи и макроскопическим телам. Однако вследствие большой массы макроскопических тел их волновые свойства не могут быть обнаружены экспериментально. Например, пылинке массой 10–9 г, движущийся со скоростью 0,5 м/с соответствует волна де Бройля с длиной волны порядка 10–21 м, т. е. приблизительно на 11 порядков меньше размеров атомов. Такая длина волны лежит за пределами доступной наблюдению области. Этот пример показывает, что макроскопические тела могут проявлять только корпускулярные свойства.
Таким образом, подтвержденная
экспериментально гипотеза де Бройля о
корпускулярно-волновом дуализме
коренным образом изменила представления
о свойствах микрообъектов.

Всем микрообъектам присущи и волновые, и корпускулярные свойства, однако, они не являются ни волной, ни частицей в классическом понимании.
Наиболее отчетливо дифракционные явления проявляются в тех случаях, когда размеры препятствия, на котором происходит дифракция волн, соизмеримы с длиной волны. Это относится к волнам любой физической природы и, в частности, к электронным волнам.
Для волн де Бройля естественной дифракционной решеткой является упорядоченная структура кристалла с пространственным периодом порядка размеров атома (приблизительно 0,1 нм).
Препятствие таких размеров (например, отверстие в непрозрачном экране) невозможно создать искусственно, но для уяснения природы волн де Бройля можно ставить мысленные эксперименты.
Рассмотрим, например, дифракцию электронов на одиночной щели ширины D

С точки зрения волновой теории, максимумы в картине дифракции электронов соответствуют наибольшей интенсивности волн де Бройля. С точки зрения корпускулярной теории, в области максимумов попадает большее число электронов.
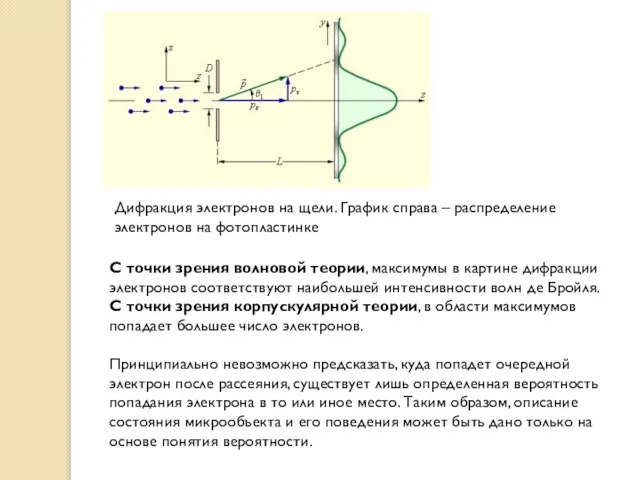
Принципиально невозможно предсказать, куда попадет очередной электрон после рассеяния, существует лишь определенная вероятность попадания электрона в то или иное место. Таким образом, описание состояния микрообъекта и его поведения может быть дано только на основе понятия вероятности.
Дифракция электронов на щели. График справа – распределение электронов на фотопластинке

Разные свойства микрообъектов не проявляются одновременно; они дополняют друг друга, и только их совокупность характеризует микрообъект полностью. В этом заключается сформулированный Н.Бором принцип дополнительности.
Можно условно сказать, что микрообъекты распространяются как волны, а обмениваются энергией как частицы.
В квантовой механике для характеристики состояний объектов в микромире вводится понятие волновой функции Ψ (пси-функции). Квадрат модуля волновой функции |Ψ|2 пропорционален вероятности нахождения микрочастицы в единичном объеме пространства.
Конкретный вид волновой функции определяется внешними условиями, в которых находится микрочастица. Математический аппарат квантовой механики позволяет находить волновую функцию частицы, находящейся в заданных силовых полях.
Безграничная монохроматическая волна де Бройля есть волновая функция свободной частицы, на которую не действуют никакие силовые поля.

Рассмотрим еще один мысленный эксперимент – дифракцию электронного пучка на двух щелях
Если в опыте по наблюдению дифракции электронов на двух щелях закрыть одну из щелей, то интерференционные полосы исчезнут, и фотопластинка зарегистрирует распределение электронов, продифрагировавших на одной щели, то есть предыдущую картинку.
Если же открыты обе щели, то появляются интерференционные полосы, и тогда возникает вопрос, через какую из щелей пролетает тот или иной электрон?
– Расскажите–ка нам отличия волновой и корпускулярной теории света. – А я не Света, я Наташа...

Психологически очень трудно смириться с тем, что ответ на этот вопрос может быть только один: электрон пролетает через обе щели.
Мы интуитивно представляем себе поток микрочастиц как направленное движение маленьких шариков и применяем для описания этого движения законы классической физики.
Но электрон (и любая другая микрочастица) обладает не только корпускулярными, но и волновыми свойствами. Легко представить, как электромагнитная световая волна проходит через две щели, т. к. волна не локализована в пространстве. Но если принять концепцию фотонов, то мы должны признать, что каждый фотон тоже не локализован.
Невозможно указать, через какую из щелей пролетел фотон, как невозможно проследить за траекторией движения фотона до фотопластинки и указать точку, в которую он попадет. Опыт показывает, что даже в том случае, когда фотоны пролетают через интерферометр поштучно, интерференционная картина после пролета многих независимых фотонов все равно возникает. Поэтому в квантовой физике делается вывод: фотон интерферирует сам с собой.

«Сновидение, вызванное полетом пчелы вокруг плода граната, за миг до пробуждения»
(Картина Сальвадора Дали)
Все вышесказанное относится и к опыту по дифракции электронов на двух щелях. Вся совокупность известных экспериментальных фактов может найти объяснение, если принять, что дебройлевская волна каждого отдельного электрона проходит одновременно через оба отверстия, в результате чего и возникает интерференция. Поштучный поток электронов тоже дает интерференцию при длительной экспозиции, т. е. электрон, как и фотон, интерферирует сам с собой.

Воистину чудно придумал всё Создатель.
Благодаря Ему и мы понять должны,
Что если на Луну не смотрит наблюдатель,
Возможно ль утверждать, что в мире нет Луны?
Возможно ль пребывать во многих точках сразу,
Привычные забыв законы бытия?
Коль спутанность частиц постичь не в силах разум,
То я и тут и там - ужель и вправду: я?
Мы многому ещё не знаем объяснений,
И как устроен свет, сказать никто не смог.
И силится понять наш человечий гений
Всё то, что за шесть дней спокойно создал Бог.