Топографическое черчение. Лекция 1

3 Блока дисциплины:
Начертательная геометрия
Инженерная графика
Топографическое черчение

В математическом энциклопедическом словаре дается следующее определение: «Начертательная геометрия – раздел геометрии, в котором пространственные фигуры, а также методы решения и исследования пространственных задач изучаются с помощью их изображений на плоскости».
Методы начертательной геометрии являются теоретической базой для решения задач технического черчения. В технике чертежи являются основным средством выражения человеческих идей. Они должны не только определять форму и размеры предметов, но и быть достаточно простыми и точными в графическом исполнении, помогать всесторонне исследовать предметы и их отдельные детали. Для того чтобы правильно выразить свои мысли с помощью рисунка, эскиза, чертежа требуется знание теоретических основ построения изображений геометрических объектов, их многообразие и отношения между ними, что и составляет предмет начертательной геометрии.
Блок 1: Начертательная геометрия

Лекция 1
Предмет начертательной
геометрии. Виды проецирования.
Точка в 2-х, 3-х плоскостях проекций.
Изображение, которое позволяет определять взаимосвязь (взаимопринадлежность) элементов объекта, называют полным.
Изображения, по которым можно определить размеры объекта, называется метрически определенными.
Из плоскостных изображений объекта наиболее широкое применение в практике получили рисунки и чертежи.
Рисунком называют изображение предмета от руки и на глаз с кажущимися относительными размерами и положениями отдельных его элементов.
Чертежом называют изображение предмета, построенное по особым правилам с помощью чертежных инструментов в точной зависимости от размеров и положения в пространстве соответствующих линий предмета.

В технике чертежи являются основным средством выражения человеческих идей. Они должны не только определять форму и размеры предметов, но и быть достаточно простыми и точными в графическом исполнении, помогать всесторонне, исследовать предметы и их отдельные детали.
Эти требования к чертежам и привели к созданию теории изображений, составляющей основу начертательной геометрии. Правила построения изображений основаны на методе проекций. Поэтому проекционный метод построения изображений является основным методом начертательной геометрии.
Итак, в курсе начертательной геометрии изучаются:
методы отображения пространственных объектов на плоскости;
способы графического и аналитического решения различных геометрических задач;
приемы увеличения наглядности и визуальной достоверности изображений проецируемого объекта;
способы преобразования и исследования геометрических свойств изображенного объекта;
основы моделирования геометрических объектов.

К проекционным изображениям в начертательной геометрии предъявляются следующие основные требования:
1. Обратимость – восстановление оригинала по его проекционным изображениям (чертежу) – возможность определять форму и размеры объекта, его положение и связь с окружающей средой.
2. Наглядность – чертеж должен создавать пространственное представление о форме предмета.
3. Точность – графические операции, выполненные на чертеже, должны давать достаточно точные результаты.
4. Простота – изображение должно быть простым по построению и допускать однозначное описание объекта в виде последовательности графических операций.

ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ
Точки в пространстве – прописными буквами латинского алфавита А,В,С,…, а также цифрами;
Линии в пространстве – строчными буквами латинского алфавита a,b,c,…
Плоскости – строчными буквами греческого алфавита – α, β, γ, δ, ε
Плоскости проекций: произвольная плоскость – π0 ,
горизонтальная – π1;
фронтальная –π2;
профильная – π 3;
любая дополнительная – π4,π5.
Оси проекций - x, y, z.
Начало координат – прописной буквой О.
Проекции точек: на горизонтальную плоскость - А′, В′, С′,…;
на фронтальную плоскость - А′′, В′′, С′′,…;
на профильную плоскость - А′′′, В′′′, С′′′;
на произвольную плоскость - А0, В0, С0,…
на дополнительную плоскость - АIV, ВIV, СIV,…
Обозначение плоскостей заданных следами:
горизонтальный след плоскости α – h0α ;
фронтальный след плоскости α – f0α ;
профильный след плоскости α – P0α.
Для проецирующих плоскостей:
α＇ - горизонтально - проецирующая плоскость;
α＂ - фронтально - проецирующая плоскость;

ВИДЫ ПРОЕЦИРОВАНИЯ
Одно из основных геометрических понятий - отображение множеств. В начертательной геометрии каждой точке трехмерного пространства ставится в соответствие определенная точка двумерного пространства – плоскости. Геометрическими элементами отображения служат точки, линии, поверхности пространства. Геометрический объект, рассматриваемый как точечное множество отображается на плоскость по закону проецирования. Результатом такого отображения является изображение объекта.

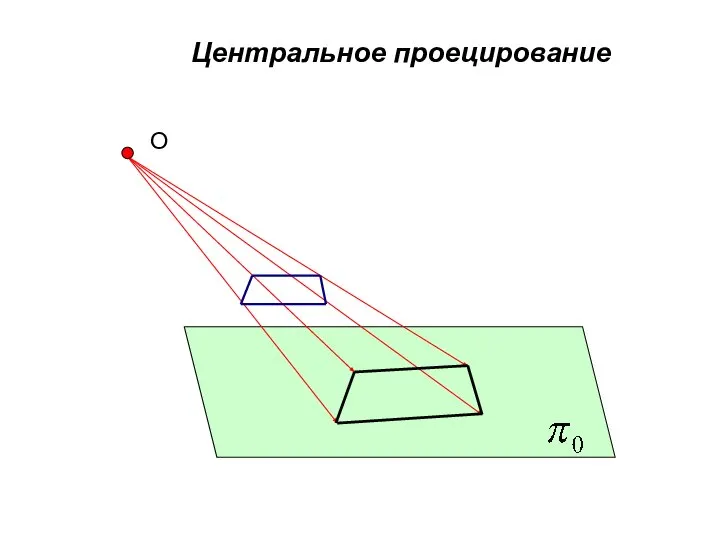
Центральное проецирование

Центральное проецирование есть наиболее общий случай проецирования геометрических объектов на плоскости.
Основными и неизменными его свойствами (инвариантами) являются следующие:
проекция точки – точка;
2) проекция прямой – прямая;
3) если точка принадлежит прямой, то проекция этой точки принадлежит проекции прямой.

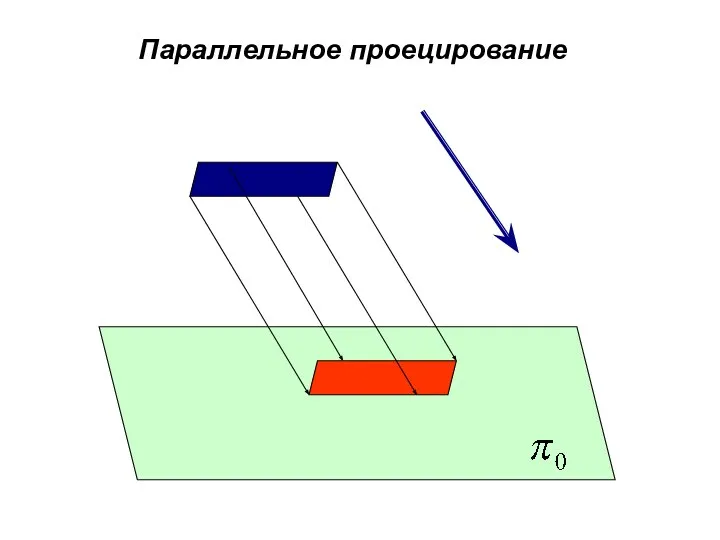
Параллельное проецирование

При параллельном проецировании сохраняются свойства центрального и добавляются следующие:
проекции параллельных прямых параллельны между собой;
отношение отрезков прямой равно отношению их проекций;
отношение отрезков двух параллельных прямых равно отношению их проекций.

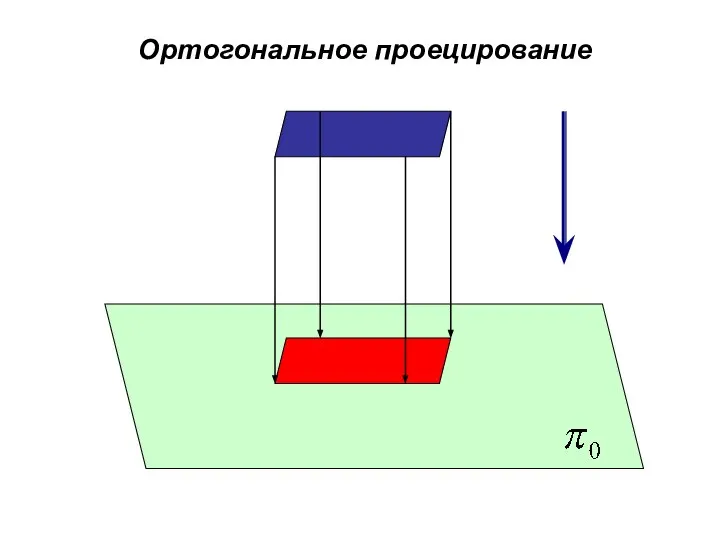
Ортогональное проецирование

Ортогональному проецированию присущи все свойства параллельного и центрального проецирования и кроме того, справедлива теорема о проецировании прямого угла:
если хотя бы одна сторона прямого угла параллельна плоскости проекций, а вторая не перпендикулярна ей, то прямой угол на эту плоскость проецируется в прямой угол.

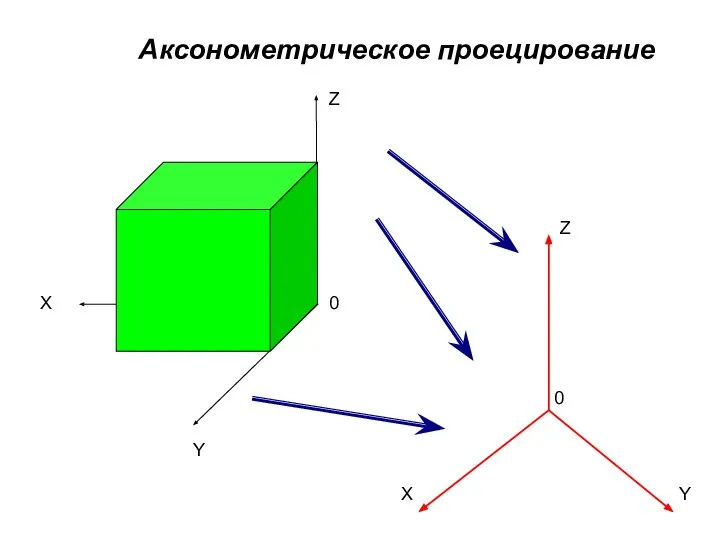
Z
X
Y
0
0
X
Y
Z
Аксонометрическое проецирование

Сущность метода параллельного аксонометрического проецирования заключается в том, что предмет относят к некоторой системе координат и затем проецируют параллельными лучами на плоскость вместе с координатной системой.

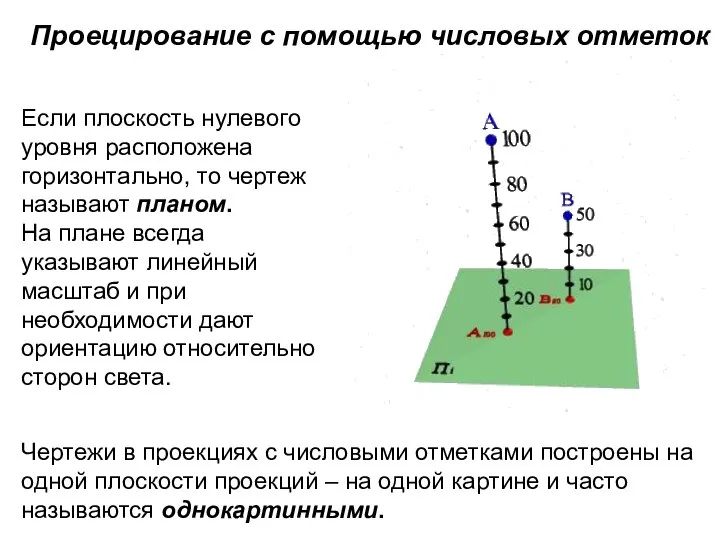
Если плоскость нулевого уровня расположена горизонтально, то чертеж называют планом.
На плане всегда указывают линейный масштаб и при необходимости дают ориентацию относительно сторон света.
Проецирование с помощью числовых отметок
Чертежи в проекциях с числовыми отметками построены на одной плоскости проекций – на одной картине и часто называются однокартинными.

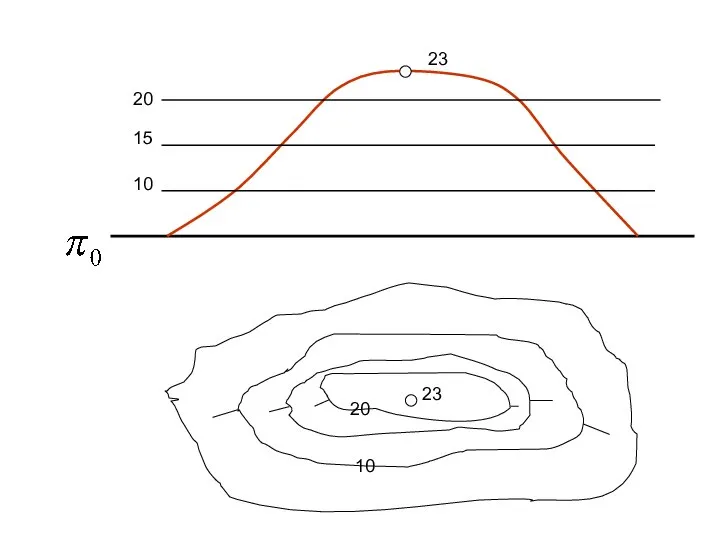
10
20
23
10
15
20
23

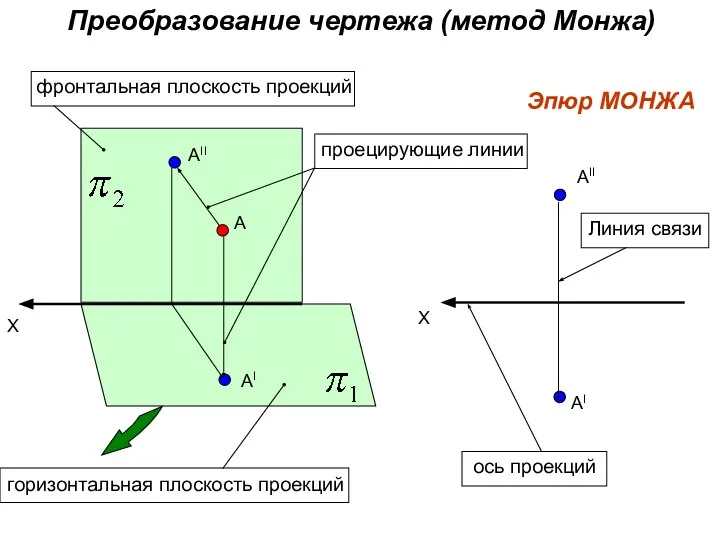
Х
А
АII
AI
AII
AI
Эпюр МОНЖА
Х
Преобразование чертежа (метод Монжа)

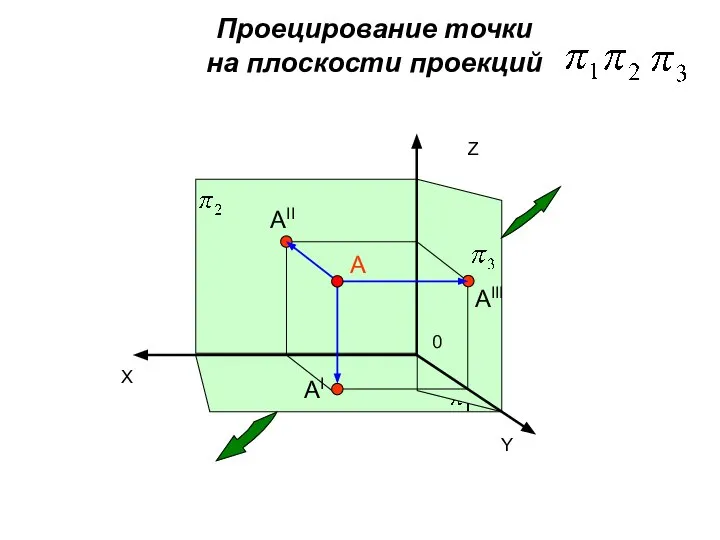
Х
А
АII
AI
АIII
Z
Y
0
Проецирование точки
на плоскости проекций

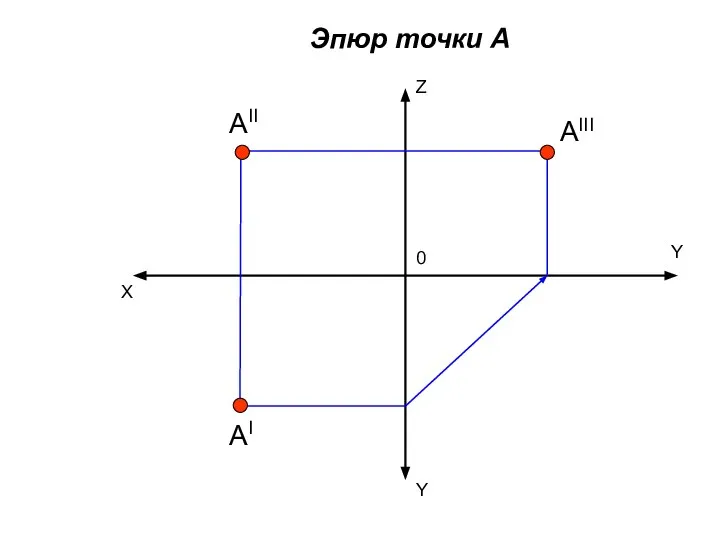
Z
X
Y
Y
0
AII
AI
AIII
Эпюр точки А

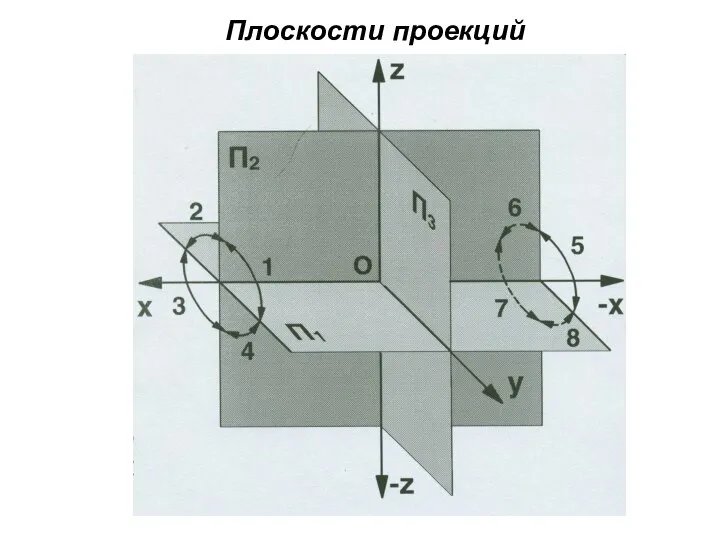
Плоскости проекций