Топологические изоляторыи смежные вопросы

План лекций
Лекция 1 - Введение
Что такое топологические изоляторы
Известные экспериментальные объекты
Эксперименты (ARPES, STM, электр.транспорт)
Лекция 2 - Кое-что о теории
- Топологические свойства зонных диэлектриков
- Общая классификация топологических фаз
Связь с проблемами спиновой жидкости и px+ipy сверхпроводящего состояния
Майорановские фермионы: как напасть на их след

Что такое топологич. изолятор - 1
Простейший пример: зонный диэлектрик (3-мерный или 2-мерный), образующий поверхностные проводящие состояния
Обобщение: любая система со щелью в спектре в объёме, но безщелевыми состояниями на поверхности (например, сверхтекучий 3He-B)

Предистория:

Гамильтониан поверхностных электронных состояний
H = v0(-i∂ - eA)σ + geffσB
зеемановский
член
двумерный градиент
вдоль поверхности
Щель в спектре пропорциональна geffBz

Сравним с графеном:
один «дираковский» фермион вместо 4-х в графене (там 2 долины и 2 проекции спина) Не работает теорема удвоения !
Псевдоспин из ур-ния Дирака – это «почти» реальный спин электрона (в графене – это индекс подрешеток, не связанный со спином)
Поэтому магнитное поле ┴ поверхности открывает щель в спектре

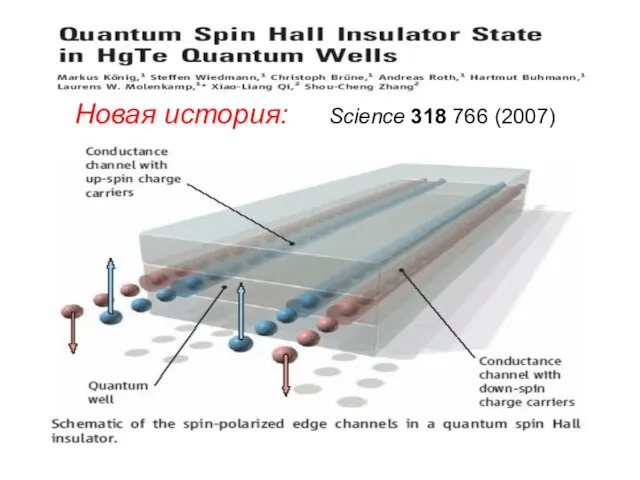
Новая история: Science 318 766 (2007)

Краевые состояния не имеют рассеяния назад
M < 0 leads to
surface anomaly

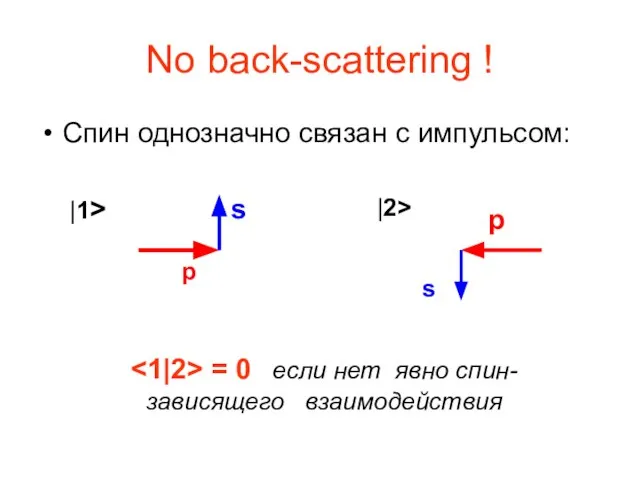
No back-scattering !
Спин однозначно связан с импульсом:
p
s
|1>
|2>
p
s
<1|2> = 0 если нет явно спин-зависящего взаимодействия

Что такое топологич. изолятор - 2
Электродинамика с Ө-членом:
Ө = π (2n+1) для сохранения Т-инвариантности
exp(iS3D)= (-1)n
для интеграла по замкнутому пространству
(изложение по материалу M. Franz, Physics 1, 36 (2008)

Что будет при Ө ≠ CONST ?
топ.
изолятор
Ө=π
простой
изолятор
Ө=0
Аномальные члены сидят на границе
Т-инвариантность там нарушена

Магнито-электрический эффект
Кроме того,
эффект Керра – вращение плоскости поляризации отраженного света

“Dynamical Axion Field in Topological Magnetic Insulators”
R. LiR. Li, J. WangR. Li, J. Wang, X. QiR. Li, J. Wang, X. Qi, S.-C. Zhang
Axions are very light, very weakly interacting particles postulated more than 30 years ago in the context of the Standard Model of particle physics. Their existence could explain the missing dark matter of the universe. However, despite intensive searches, they have yet to be detected. In this work, we show that magnetic fluctuations of topological insulators couple to the electromagnetic fields exactly like the axions, and propose several experiments to detect this dynamical axion field. In particular, we show that the axion coupling enables a nonlinear modulation of the electromagnetic field, leading to attenuated total reflection. We propose a novel optical modulators device based on this principle.
Arxiv: 0908.1537

Объекты, известные как Топологические Изоляторы
или Топ. Сверхпроводники
2D: HgTe (квантовые ямы с 2D электронами)
3D: Bi1-xSbx Bi2Se3 Bi2Te3 Tl Bi Se2
3He-B Н.Копнин et al J.LowTemp.Phys. 85, 267 (1991)
Г.Воловик Письма ЖЭТФ 90, 440 (2009).
Topological superfluid 3He-B: fermion zero modes on interfaces and
in the vortex core M.A. Silaevin the vortex core M.A. Silaev, G.E. Volovik arXiv:1005.4672

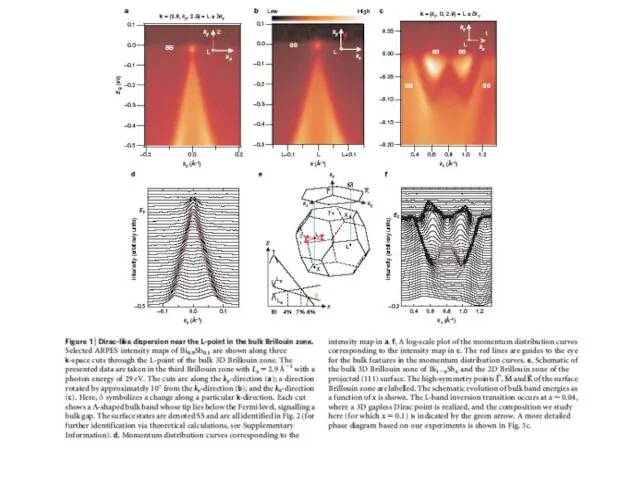
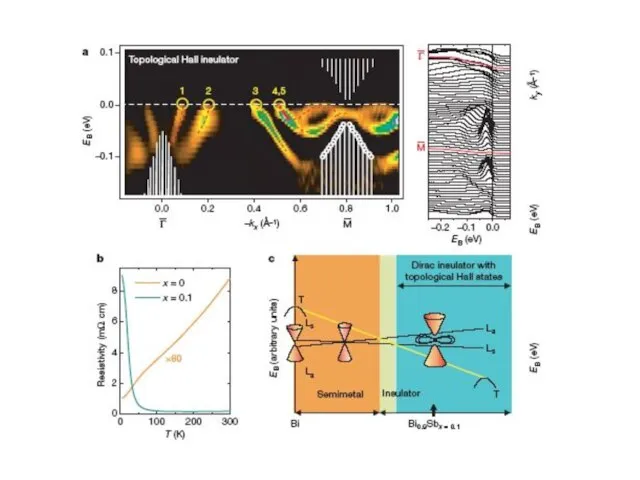
Эксперименты ARPES

arXiv:08122078
arXiv:08122078

Band structure calculation
Band structure calculation

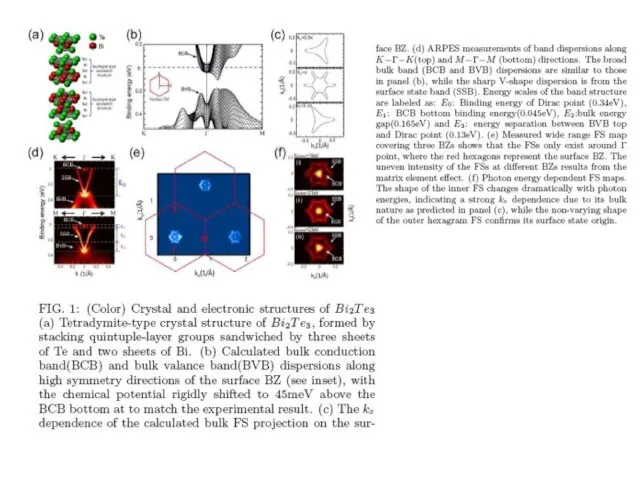
Large Gap Topological Insulator Bi2Te3 with a Single Dirac Cone on the Surface
Y. L. ChenY. L. Chen, J. G. AnalytisY. L. Chen, J. G. Analytis, J. H. ChuY. L. Chen, J. G. Analytis, J. H. Chu, Z. K. LiuY. L. Chen, J. G. Analytis, J. H. Chu, Z. K. Liu, S. K. MoY. L. Chen, J. G. Analytis, J. H. Chu, Z. K. Liu, S. K. Mo, X. L. QiY. L. Chen, J. G. Analytis, J. H. Chu, Z. K. Liu, S. K. Mo, X. L. Qi, H. J. ZhangY. L. Chen, J. G. Analytis, J. H. Chu, Z. K. Liu, S. K. Mo, X. L. Qi, H. J. Zhang, D. H. LuY. L. Chen, J. G. Analytis, J. H. Chu, Z. K. Liu, S. K. Mo, X. L. Qi, H. J. Zhang, D. H. Lu, X. DaiY. L. Chen, J. G. Analytis, J. H. Chu, Z. K. Liu, S. K. Mo, X. L. Qi, H. J. Zhang, D. H. Lu, X. Dai, Z. FangY. L. Chen, J. G. Analytis, J. H. Chu, Z. K. Liu, S. K. Mo, X. L. Qi, H. J. Zhang, D. H. Lu, X. Dai, Z. Fang, S. C. ZhangY. L. Chen, J. G. Analytis, J. H. Chu, Z. K. Liu, S. K. Mo, X. L. Qi, H. J. Zhang, D. H. Lu, X. Dai, Z. Fang, S. C. Zhang, I. R. FisherY. L. Chen, J. G. Analytis, J. H. Chu, Z. K. Liu, S. K. Mo, X. L. Qi, H. J. Zhang, D. H. Lu, X. Dai, Z. Fang, S. C. Zhang, I. R. Fisher, Z. HussainY. L. Chen, J. G. Analytis, J. H. Chu, Z. K. Liu, S. K. Mo, X. L. Qi, H. J. Zhang, D. H. Lu, X. Dai, Z. Fang, S. C. Zhang, I. R. Fisher, Z. Hussain, Z. X. Shen
arXiv:0904.1829

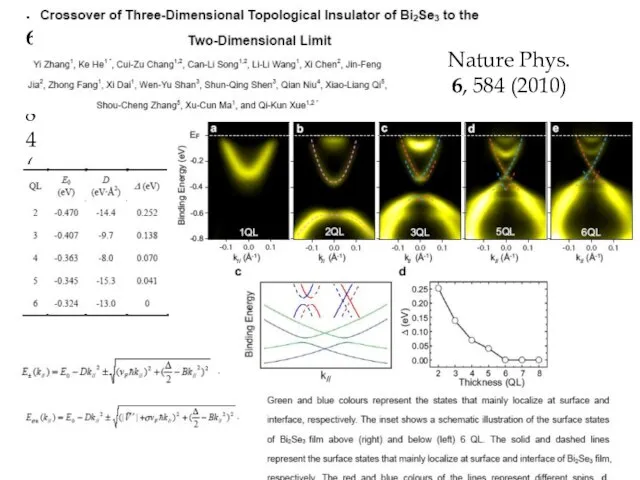
Nature Phys.
6, 584 (2010)
Nature Phys.
6, 584 (2010)

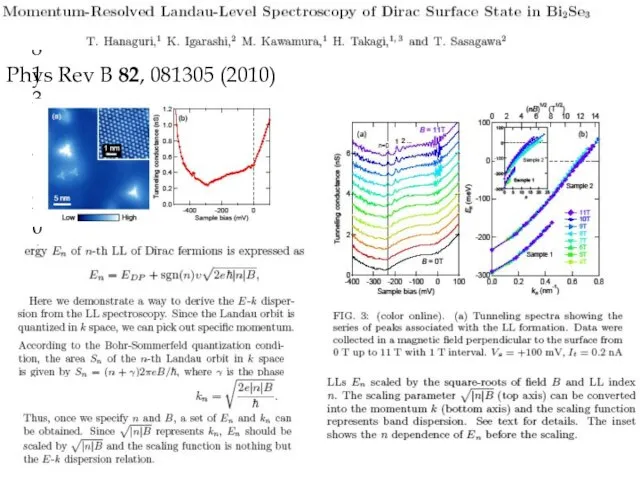
Phys Rev B 82, 081305 (2010)
Phys Rev B 82, 081305 (2010)

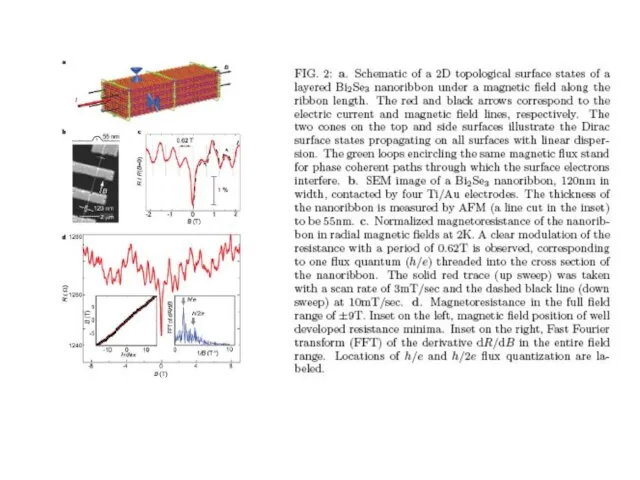
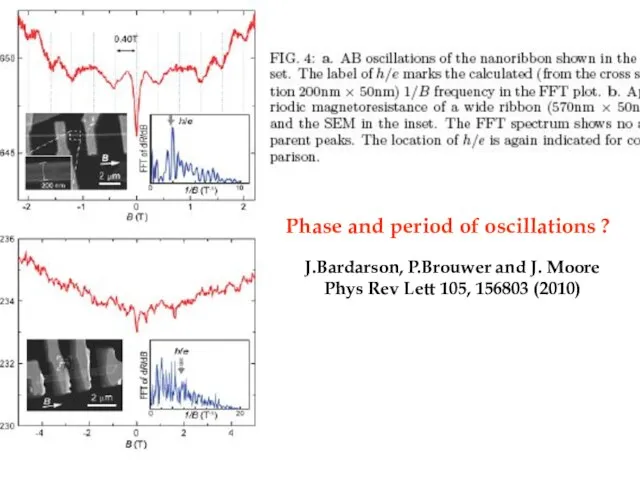
Транспортные эксперименты
Aharonov-Bohm interference in topological insulator nanoribbons
Hailin PengHailin Peng, Keji LaiHailin Peng, Keji Lai, Desheng KongHailin Peng, Keji Lai, Desheng Kong, Stefan MeisterHailin Peng, Keji Lai, Desheng Kong, Stefan Meister, Yulin Chen,
Xiao-Liang Qi Xiao-Liang Qi, Shou-Cheng Zhang Xiao-Liang Qi, Shou-Cheng Zhang, Zhi-Xun Shen Xiao-Liang Qi, Shou-Cheng Zhang, Zhi-Xun Shen, Yi Cui
arXiv:0908.3314
Giant magnetic fingerprint in non-metallic Bi2Se3
J.Checkelsky et al arXiv:0909.1840
Superconductivity in CuxBi2Se3 and its implications for pairing in the
undoped topological insulator Y. S. Hor Y. S. Hor, A. J. Williams Y. S. Hor, A. J. Williams, J. G. Checkelsky,
P. RoushanP. Roushan, J. SeoP. Roushan, J. Seo, Q. XuP. Roushan, J. Seo, Q. Xu, H. W. ZandbergenP. Roushan, J. Seo, Q. Xu, H. W. Zandbergen, A. YazdaniP. Roushan, J. Seo, Q. Xu, H. W. Zandbergen, A. Yazdani, N. P. OngP. Roushan, J. Seo, Q. Xu, H. W. Zandbergen, A. Yazdani, N. P. Ong, R. J. Cava
arXiv:0909.2890
Nonlocal transport in quantum spin-Hall state in HgTe quantum well

Phase and period of oscillations ?
Phase and period of oscillations ?
J.Bardarson, P.Brouwer and J. Moore
Phys Rev Lett 105, 156803 (2010)

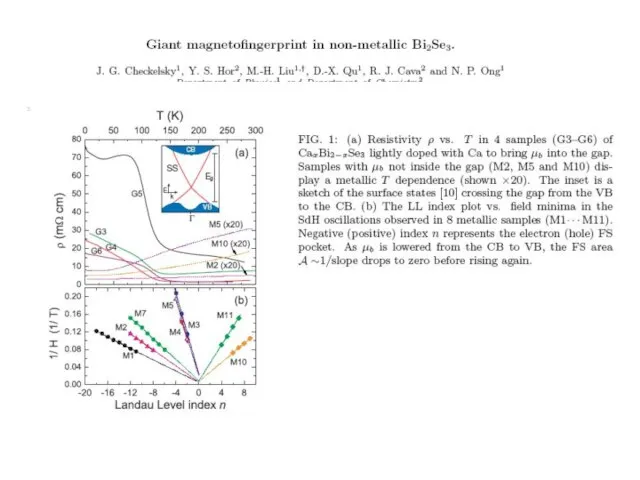
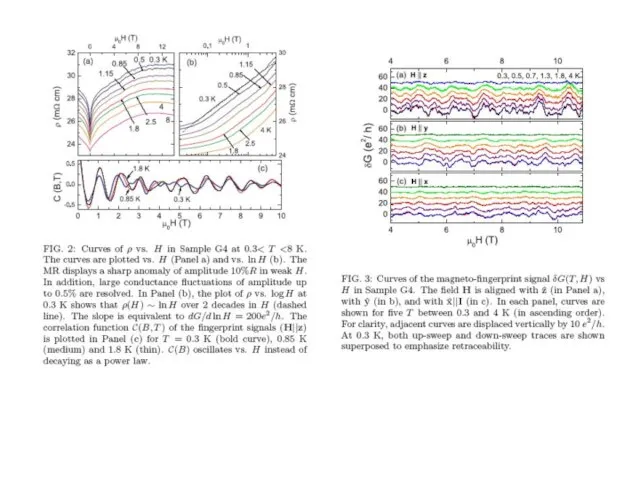
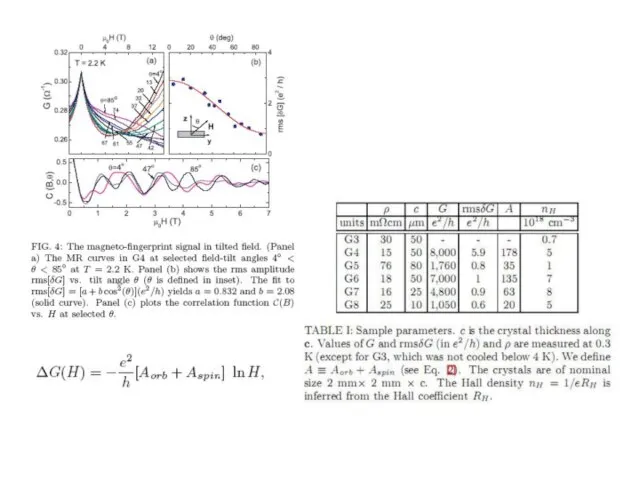
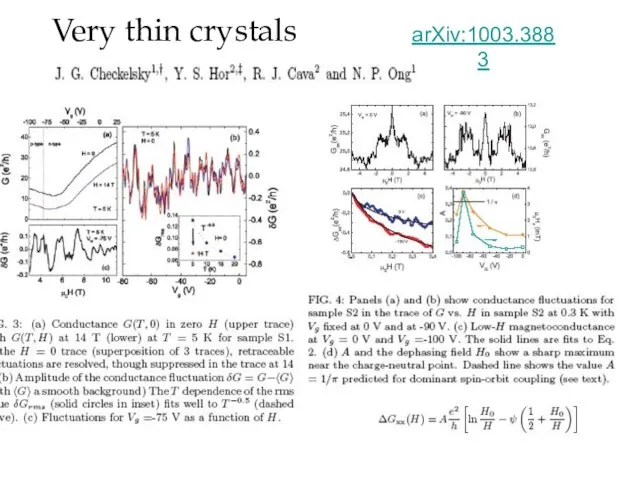
Very thin crystals
arXiv:1003.3883

Лекция 2. Теория
Топологические свойства зонных диэлектриков
Общая классификация возможных топологических фаз в размерностях d=1,2,3
Связь с проблемами спиновой жидкости и px+ipy сверхпроводящего состояния
Майорановские фермионы:
как напасть на их след

Теория зонных ТИ
Общая топологическая классификация
Топологические калибровочные теории
Arxiv:1011.3485

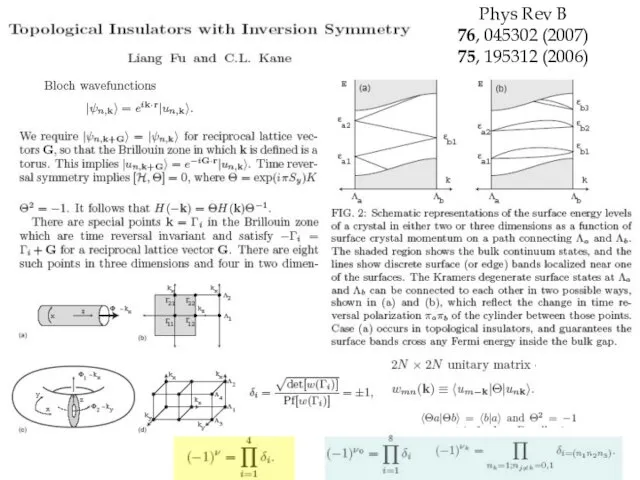
Phys Rev B
76, 045302 (2007)
75, 195312 (2006)
2D:

Непрерывный предел: 0< m +2 << 1

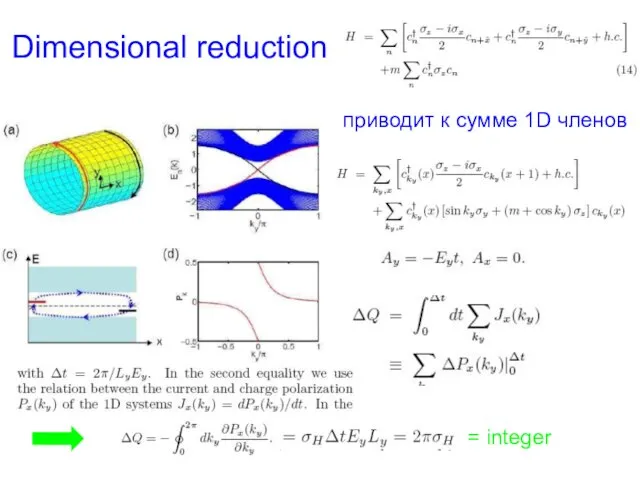
Dimensional reduction
приводит к сумме 1D членов
= integer

Магнитоэлектрический эффект
в присутствии щели на пов-сти
Для бесщелевой поверхности выведено
эффективное действие с дираковскими фермионами

Singe Dirac point on
the sphere
Singe Dirac point on
the sphere
Как это совместить с открытием
щели в тонкой пластинке ?

Туннель для связи с антиподами
Тонкая бесконечная пластинка ТИ
На верхней и нижней поверхностях живут дираковские электроны
(как в графене, но нет 4-вырождения)
Yi ZhangYi Zhang, Ying RanYi Zhang, Ying Ran, Ashvin Vishwanath arxiv:0904.0690
Сквозной туннель радиуса R содержит на внутренней поверхности состояния со спектром
n = m + ½ - (Φ/Φ0)
m – целое число

General classification: A.Kitaev, A.Ludwig et al

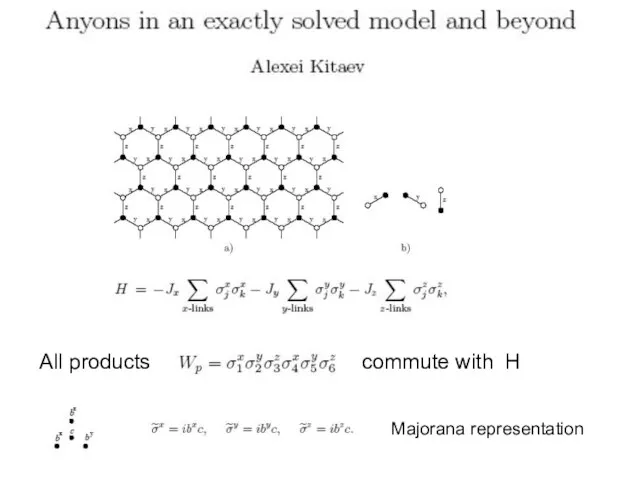
Connections to spin-liquids and p+ip superconductors
Основы:
Недавние работы
Phys. Rev. B 79, 180501(R) (2009)
Exactly solvable pairing model for superconductors with px+ipy-wave symmetry
M. IbañezM. Ibañez, Jon LinksM. Ibañez, Jon Links, G. SierraM. Ibañez, Jon Links, G. Sierra, and S.-Y. Zhao
Gauge symmetry in Kitaev-type spin models and index theorems on
odd manifolds Yue Yu arXiv:0704.3829 Nucl. Phys. B 799, 345 (2008)

All products
commute with H
Majorana representation

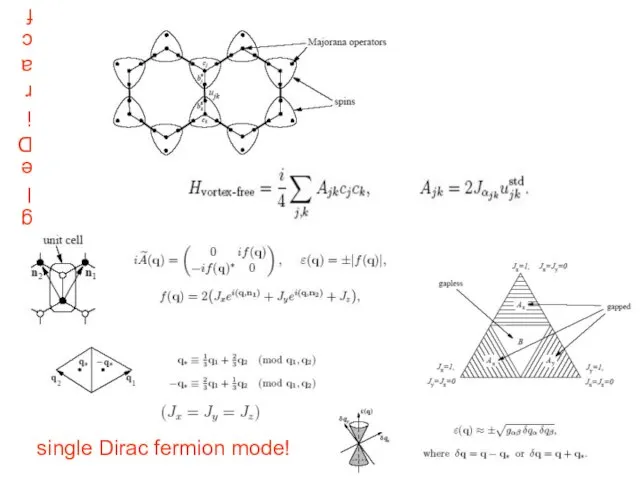
single Dirac fermion mode!
single Dirac fermion mode!

B-phase can be made gapful
1) Including of magnetic field, or NNN fermionic couplings (Kitaev 2006)
2) Going to decorated honeycomb lattice
(Yao-Kivelson 2007)
Chern number

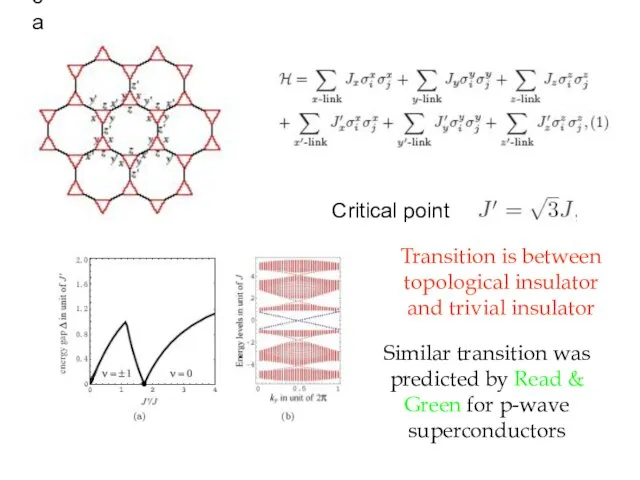
Critical point
Critical point
Transition is between topological insulator and trivial insulator
Similar transition was predicted by Read & Green for p-wave superconductors

Майорановские состояния в
центрах сверхпроводящих вихрей и
неабелева обменная статистика
D.A.Ivanov PRL 2001
4 vortices:
Non-Ab trans.

Superconducting Proximity Effect and Majorana Fermions at the Surface of a Topological Insulator
Phys. Rev. Lett. 100, 096407 (2008) L. FuL. Fu and C. L. Kane
Bi2Se3
Nb
Chiral
states

Аналогия (неполная)
с px+ipy сверхпроводником
H =
Time-reversal operator
original fermions
chiral fermions
Due to phase factors the current Hamiltonian (1) is T-inv.
whereas px+ipy superconductor breaks T-invariance
(1)

Сверхпроводящий эффект близости на поверхности ТИ
С учетом примесного рассеяния на поверхности,
которое не должно приводить к распариванию
(из-за того, что T-инвариантность не нарушена)
Nb
Nb
Зависимость Ic(L,T) - способ измерить коэфф. диффузии поверхностных состояний
Эксперимент B.Sacepe et al – джозеф. ток на поверхности

Индуцированная сверхпроводимость и майорановские состояния
Superconducting Proximity Effect and Majorana Fermions at the Surface of a Topological Insulator
Phys. Rev. Lett. 100, 096407 (2008) L. FuL. Fu and C. L. Kane
Они же: arXiv:0804.4469, arXiv:0903.2427
Phys. Rev. Lett. 102, 216404 (2009) Electrically Detected Interferometry of Majorana Fermions in a Topological Insulator A. R. AkhmerovA. R. Akhmerov, Johan NilssonA. R. Akhmerov, Johan Nilsson, and C. W. J. Beenakker
Manipulation of Majorana fermion, Andreev reflection and Josephson current on topological insulators Yukio TanakaYukio Tanaka, Takehito YokoyamaYukio Tanaka, Takehito Yokoyama, Naoto Nagaosa arXiv:0907.2088
Majorana Fermion Induced Resonant Andreev Reflection K. T. LawMajorana Fermion Induced Resonant Andreev Reflection K. T. Law, Patrick A. LeeMajorana Fermion Induced Resonant Andreev Reflection K. T. Law, Patrick A. Lee, T. K. Ng arXiv:0907.1909
Detecting Majorana bound states induced by a topological insulator
Colin Benjamin Colin Benjamin, Jiannis K. Pachos arXiv:0908.0655