Слайд 2Трептенията са най-често срещаните механични движения. Те са навсякъде около нас.

Слайд 4 Що е трептене?
Движение, което се повтаря през равни интервали от време и
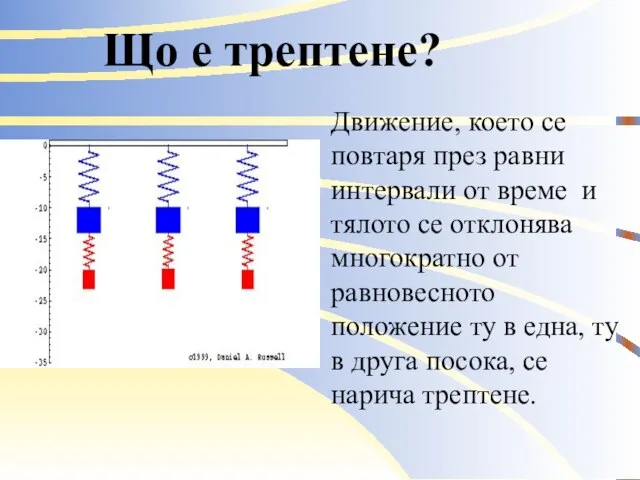
тялото се отклонява многократно от равновесното положение ту в една, ту в друга посока, се нарича трептене.
Слайд 5Собствени(свободни) трептения
Трептения, които възникват под действие на вътрешни сили, след извеждане на
системата от равновесното положение.
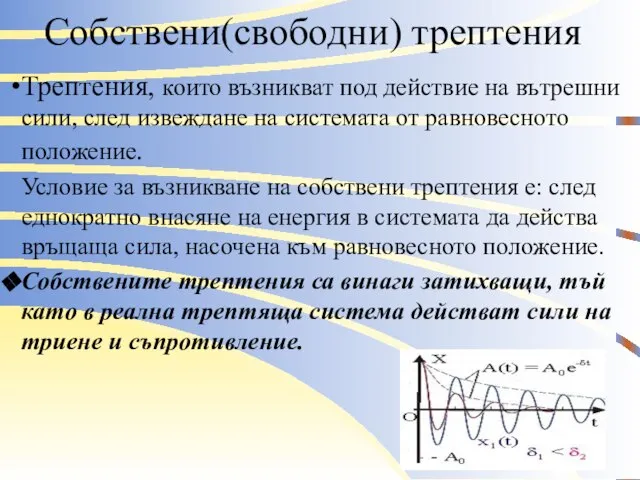
Условие за възникване на собствени трептения е: след еднократно внасяне на енергия в системата да действа връщаща сила, насочена към равновесното положение.
Собствените трептения са винаги затихващи, тъй като в реална трептяща система действат сили на триене и съпротивление.
Слайд 6Хармонично трептене
Трептене, което се извършва под действие на сила F = -k.x,
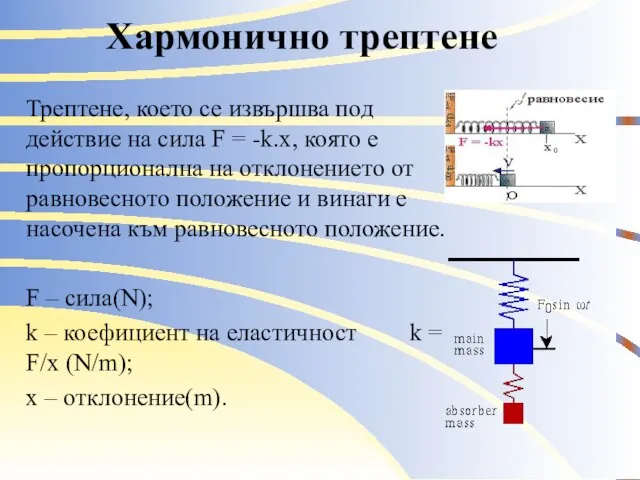
която е пропорционална на отклонението от равновесното положение и винаги е насочена към равновесното положение.
F – сила(N);
k – коефициент на еластичност k = F/x (N/m);
х – отклонение(m).
Слайд 7Характеристики и графика на хармонично трептене
Амплитуда [А(m)] – max отклонение;
Период [Т(s)] –
![Характеристики и графика на хармонично трептене Амплитуда [А(m)] – max отклонение; Период](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/389870/slide-6.jpg)
времето за едно пълно трептене;
Честота [υ(Hz)] – броят на трептенията за единица време.
υ = 1/ Т; 1Hz = 1s-1
Графиката изразява зависимостта на отклонението (х) от времето (t).
Слайд 8 Енергия на хармоничното трептене
Еластична потенциална енергия – дължи се на силата
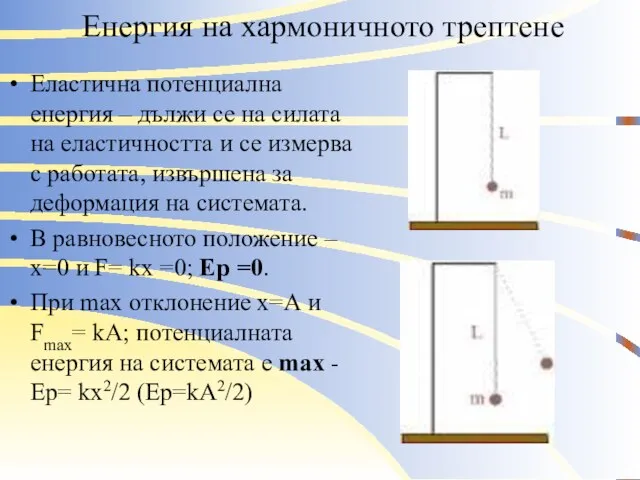
на еластичността и се измерва с работата, извършена за деформация на системата.
В равновесното положение – х=0 и F= kx =0; Ep =0.
При max отклонение х=А и Fmax= kA; потенциалната енергия на системата e max - Ep= kx2/2 (Ep=kA2/2)
Слайд 9Енергия на хармоничното трептене
При трептенето кинетичната енергия в точката на max отклонение

от равновесното положение е: Ек = 0.
В момента на преминаване през равновесното положение кинетичната енергия достига своя max: Eк = mv2/2
При хармоничното трептене става периодично превръщане на: Ек –> Ep и Ep -> Eк.
Слайд 10Енергия на хармоничното трептене
Пълна механична енергия: Е = Еp + Ек =

const.
E = Ep, в момента на max отклонение от равновесното положение; (Е=Ер = кх2/2)
Е = Ек, в момента на преминаване през равновесното положение. (Е=Eк = mv2/2)
Извод: При хармоничното трептене винаги се извършва периодично превръщане на потенциалната енергия в кинетична и обратно, но пълната енергия на трептящата система една и съща, ако няма триене и съпротивление.
Слайд 11Прости трептящи системи
Пружинно махало – ситема от пружина и окачено на нея

тяло.(http://dw.georgievi.net/ivan/spring-dyn-model.html)
Слайд 12Прости трептящи системи
Математично махало – малко тежко топче, окачено на дълга, тънка
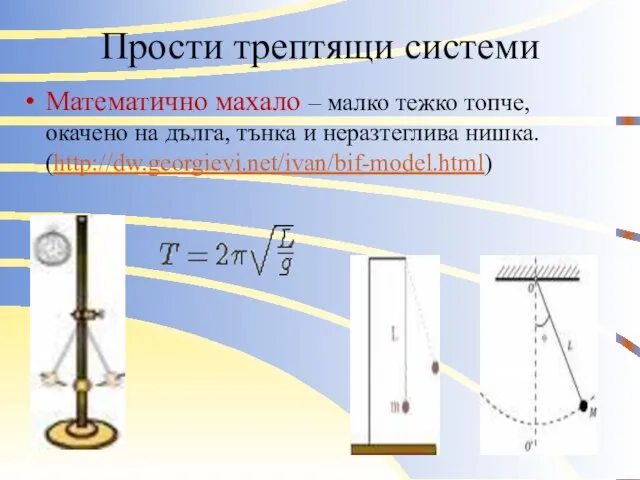
и неразтеглива нишка. (http://dw.georgievi.net/ivan/bif-model.html)
Слайд 13Принудени трептения
Трептения, които се извършват под действие на външна, периодично изменяща се

сила.
Те са незатихващи, защото загубата на енергия се компенсира от външни сили.
Слайд 14Резонанс
Явление, при което амплитудата на принудените трептения става max, когато честотата на
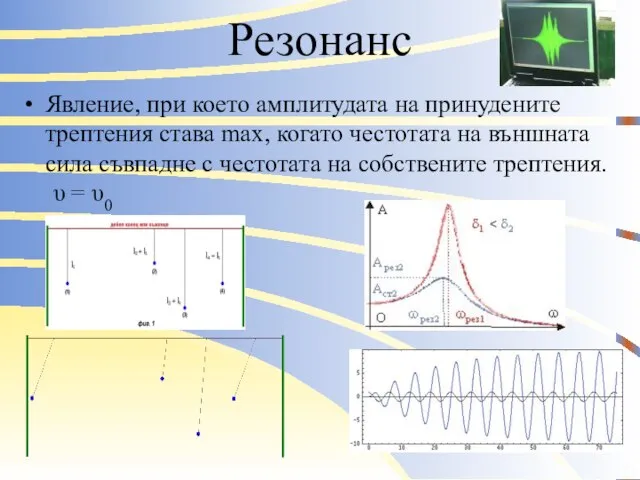
външната сила съвпадне с честотата на собствените трептения. υ = υ0
Слайд 15Защо при резонанс А на трептенията е максимална?
Създават се най-благоприятни условия за

предаване на енергия от източник.
Външната сила извършва положителна работа над трептящата система през целия период от време.( При всяка друга честота ≠ от резанансната, външната сила извършва отрицателна работа, намалявайки енергията на системата през голяма част от времето.)
Слайд 16Приложения на резонанса
Честотомери –уреди за измерване υ на променлив ток.
За усилване на

звука при музикалните инструменти.
Безжично предаване на енергия.
Слайд 17 Вредното действие на резонанса
Разрушаване на тела, конструкции.
Опасни последици за човека(при υ=5-7Hz).






![Характеристики и графика на хармонично трептене Амплитуда [А(m)] – max отклонение; Период](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/389870/slide-6.jpg)










 Техники эффективного обучения
Техники эффективного обучения История успеха HYAMATRIX
История успеха HYAMATRIX Эпоха возрождения
Эпоха возрождения Реклама - двигатель торговли
Реклама - двигатель торговли ВОЙНОВА АНАСТАСИЯ группа МЭ082
ВОЙНОВА АНАСТАСИЯ группа МЭ082 Виртуальная экскурсия «Школьный мемориальный музей «памяти О.Е.Филипповой»»
Виртуальная экскурсия «Школьный мемориальный музей «памяти О.Е.Филипповой»» Баскетбол
Баскетбол 3f1245a5185fb3888a173f44c6e85193
3f1245a5185fb3888a173f44c6e85193 Семья – глаза в глаза
Семья – глаза в глаза Шестнадцатеричная_система_счисления
Шестнадцатеричная_система_счисления Базовой курс информатики
Базовой курс информатики Презентация на тему Сложение скоростей
Презентация на тему Сложение скоростей Запорожье
Запорожье Архитектура ЭВМ. Логические основы ЭВМ
Архитектура ЭВМ. Логические основы ЭВМ Урок-практикум.Обобщение изученного материала. Подготовка к ЕГЭ.«Это непростое простое повторение?!...» 11 класс.
Урок-практикум.Обобщение изученного материала. Подготовка к ЕГЭ.«Это непростое простое повторение?!...» 11 класс. МОСКВА 2012
МОСКВА 2012 Итоги проведения областной олимпиады и конкурса профессионального мастерства 2021г
Итоги проведения областной олимпиады и конкурса профессионального мастерства 2021г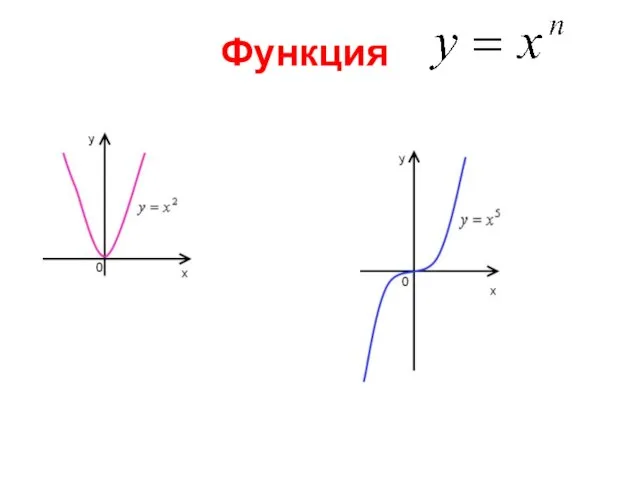 Функция
Функция Презентация на тему Загрязнение вод
Презентация на тему Загрязнение вод  3 причины освоить скорочтение
3 причины освоить скорочтение Презентация на тему Общение как понимание урок 10 класс
Презентация на тему Общение как понимание урок 10 класс Сім_я
Сім_я "Б У С Ы"
"Б У С Ы" Влияние курения на центральную нервную систему в подростковом периоде. Выполнила: Пименова Анастасия,
Влияние курения на центральную нервную систему в подростковом периоде. Выполнила: Пименова Анастасия,  Оценка временной стоимости денег в общественном секторе экономики
Оценка временной стоимости денег в общественном секторе экономики Жирные кислоты
Жирные кислоты Найти обстоятельства
Найти обстоятельства Пасхальные традиции в России
Пасхальные традиции в России