Тригонометрические функции, их графики и свойства

Функция y = sin x
График функции y = sin x
Свойства функции:
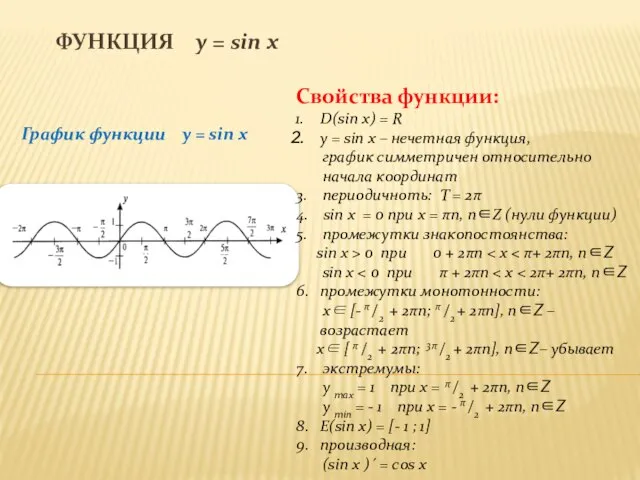
D(sin x) = R
y = sin x – нечетная функция,
график симметричен относительно
начала координат
3. периодичноть: T = 2π
4. sin x = 0 при х = πn, nZ (нули функции)
5. промежутки знакопостоянства:
sin x > 0 при 0 + 2πn < x < π+ 2πn, nZ
sin x < 0 при π + 2πn < x < 2π+ 2πn, nZ
6. промежутки монотонности:
x [- π /2 + 2πn; π /2 + 2πn], nZ – возрастает
x [ π /2 + 2πn; 3π /2 + 2πn], nZ– убывает
7. экстремумы:
y max = 1 при х = π /2 + 2πn, nZ
y min = - 1 при х = - π /2 + 2πn, nZ
8. E(sin x) = [- 1 ; 1]
9. производная:
(sin x )´ = cos x

y
x
1
-1
π/2
-π/2
π
3π/2
2π
-π
-3π/2
-2π
0
y = sin x +1
y = sin x
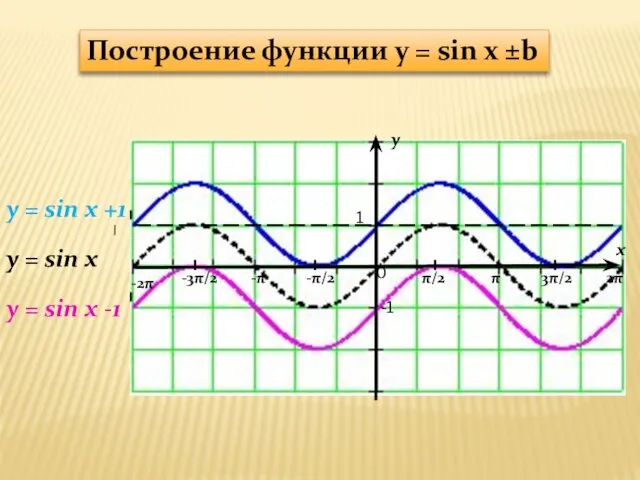
Построение функции y = sin x ±b
y = sin x -1

y
x
1
-1
π/2
-π/2
π
3π/2
2π
-π
-3π/2
-2π
0
y = sin(x +π/2)
y = sin x
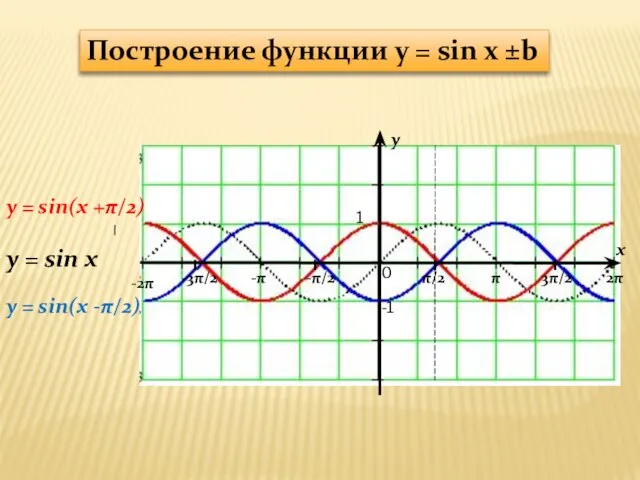
Построение функции y = sin x ±b
y = sin(x -π/2)

Функция y = cos x
График функции y = cos x
Свойства функции:
D(cos x) = R
y = cos x – четная функция,
график симметричен относительно
оси ординат
3. периодичноть: T = 2π
4. cos x = 0 при х = π /2 + πn, nZ (нули функции)
5. промежутки знакопостоянства:
cos x > 0 при - π /2 + 2πn < x < π /2 + 2πn, nZ
cos x < 0 при π /2 + 2πn < x < 3π /2 + 2πn, nZ
6. промежутки монотонности:
x [ π+ 2πn; 2π+ 2πn], nZ – возрастает
x [0 + 2πn; π+ 2πn], nZ– убывает
7. экстремумы:
y max = 1 при х = 2πn, nZ
y min = - 1 при х = π+ 2πn, nZ
8. E(cos x) = [- 1 ; 1]
9. производная:
(cos x )´ = - sin x

y
x
1
-1
π/2
-π/2
π
3π/2
2π
-π
-3π/2
-2π
0
y = cos x +1
y = cos x
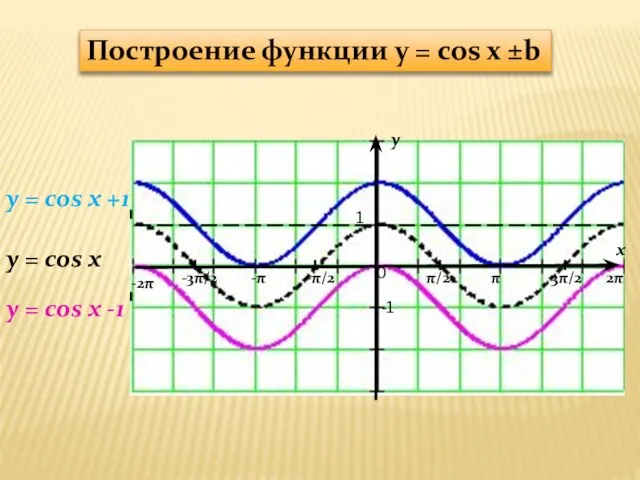
Построение функции y = cos x ±b
y = cos x -1

y
x
1
-1
π/2
-π/2
π
3π/2
2π
-π
-3π/2
-2π
0
y = cos(x -π/2)
y = cos x
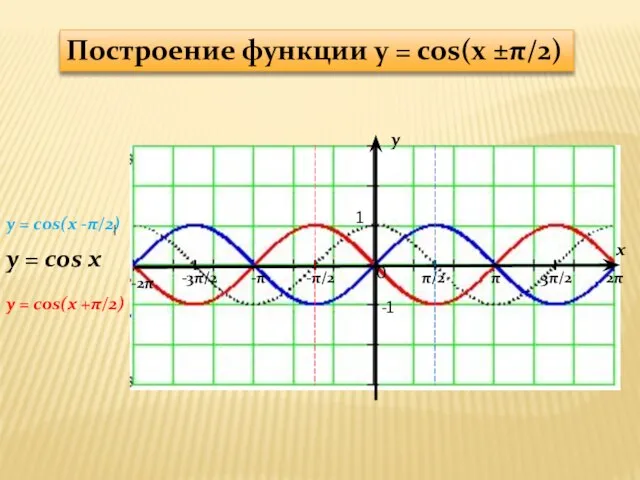
Построение функции y = cos(x ±π/2)
y = cos(x +π/2)

Функция y = tg x
График функции y = tg x
Свойства функции:
D(tg x) = x R/ π /2 + πn, nZ
y = tg x – нечетная функция
график симметричен относительно
начала координат
3. периодичноть: T = π
4. tg x = 0 при х = πn, nZ (нули функции)
5. промежутки знакопостоянства:
tg x > 0 при 0 + πn < x < π /2 + πn, nZ
tg x < 0 при - π /2 + πn < x < 0 + πn, nZ
6. промежутки монотонности:
x [- π /2 + πn; π /2 + πn], nZ – возрастает
экстремумов нет
E(tg x) = R
9. производная:
(tg x )´ = 1/cos 2 x