Презентация на тему:Элементы Комбинаторики!!!

Студента Группы ПР – 101(К) Савченко А.А
Проверила Малыгина Г.С.

Комбинаторика!
(Комбинаторный анализ) — раздел математики, изучающий дискретные объекты, множества (сочетания,перестановки, размещения и перечисления элементов) и отношения на них (например, частичного порядка). Комбинаторика связана со многими другими областями математики — алгеброй, геометрией, теорией вероятностей, и имеет широкий спектр применения в различных областях знаний (например в генетике, информатике, статистической физике).
Термин «комбинаторика» был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве».

Методы Комбинаторики
Перестановкой из n элементов (например чисел 1,2,…,n) называется всякий упорядоченный набор из этих элементов. Перестановка также является размещением из n элементов по n.
Сочетанием из n по k называется набор k элементов, выбранных из данных n элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.
Композицией числа n называется всякое представление n в виде упорядоченной суммы целых положительных чисел.
Разбиением числа n называется всякое представление n в виде неупорядоченной суммы целых положительных чисел.

Комбинаторные задачи
Комбинаторика – от латинского слова combinare, что означает «соединять, сочетать».
Методы комбинаторики находят широкое применение в физике, химии, биологии, экономики и др. областях знания.
Комбинаторику можно рассматривать как часть теории множеств – любую комбинаторную задачу можно свести к задаче о конечных множествах и их отображениях.

I. Уровни решения комбинаторных задач
1. Начальный уровень.
Задачи поиска хотя бы одного решения, хотя бы одного расположения объектов, обладающих заданным свойствами
- отыскание такого расположения десяти точек на пяти отрезках, при котором на каждом отрезке лежит по четыре точки;
- такого расположения восьми ферзей на шахматной доске, при котором они не бьют друг друга.
Иногда удаётся доказать, что данная задача не имеет решения
(например, нельзя расположить 10 шаров в 9 урнах так, что
бы в каждой урне было не более одного шара – хотя бы в
одной урне окажется не менее двух шаров).

2. Второй уровень.
Если комбинаторная задача имеет несколько решений, то возникает вопрос о подсчете числа таких решений, описании всех решений данной задачи.
3. Третий уровень.
Решения данной комбинаторной задачи отличаются друг от друга некоторыми параметрами. В этом случае возникает вопрос отыскания оптимального варианта решения такой задачи.
Например:
Путешественник хочет выехать из города А, посетить города В, С, и D. После чего вернуться в город А.

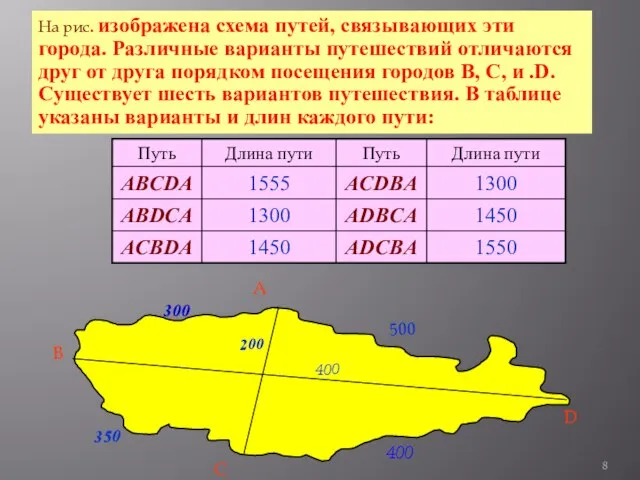
На рис. изображена схема путей, связывающих эти города. Различные варианты путешествий отличаются друг от друга порядком посещения городов В, С, и .D. Существует шесть вариантов путешествия. В таблице указаны варианты и длин каждого пути:

Правила суммы и произведения
1. Сколько различных коктейлей можно составить из четырёх напитков, смешивая их в равных количествах по два?
AB, AC, AD, BC, BD, CD – всего 6 коктейлей
2. Сколько различных двузначных чисел можно составить из цифр 0, 1, 2, 3 ?
Первой цифрой двузначного числа может одна из цифр 1, 2, 3 (цифра 0 не
может быть первой). Если первая цифра выбрана, то вторая может быть любая из
цифр 0, 1, 2, 3. Т.к. каждой выбранной первой соответствует четыре способа
выбора второй, то всего имеется
4 + 4 + 4 = 4·3 = 12 различных двузначных чисел.
А
D
С
В

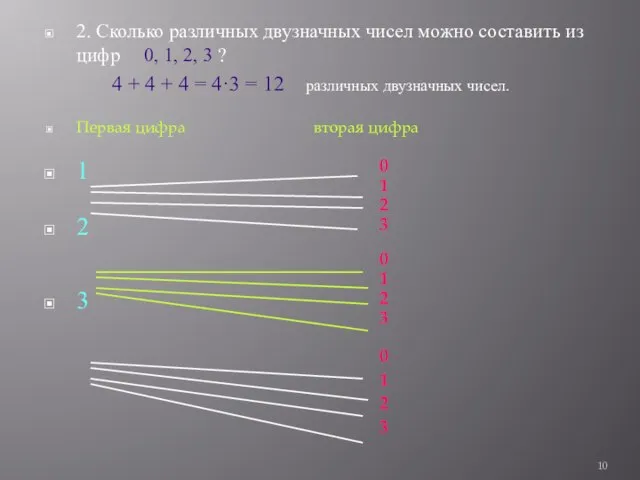
2. Сколько различных двузначных чисел можно составить из цифр 0, 1, 2, 3 ?
4 + 4 + 4 = 4·3 = 12 различных двузначных чисел.
Первая цифра вторая цифра
1
2
3
0
1
2
3
0
1
2
3
0
1
2
3

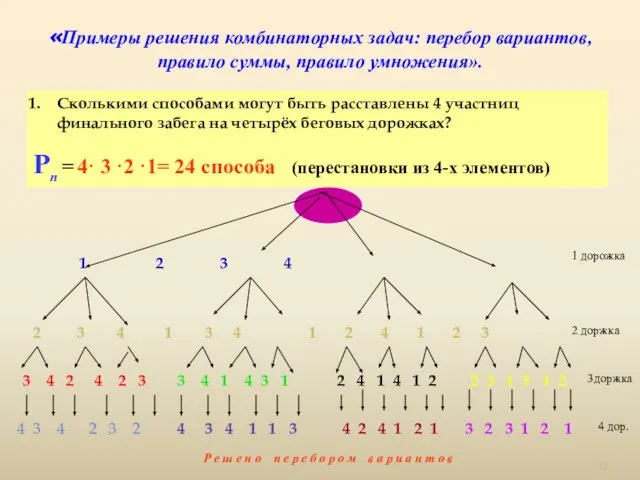
«Примеры решения комбинаторных задач: перебор вариантов, правило суммы, правило умножения».
Сколькими способами могут быть расставлены 4 участниц финального забега на четырёх беговых дорожках?
Рп = 4· 3 ·2 ·1= 24 способа (перестановки из 4-х элементов)
1 2 3 4
2 3 4 1 3 4 1 2 4 1 2 3
3 4 2 4 2 3
4 3 4 2 3 2
3 4 1 4 3 1
4 3 4 1 1 3
2 4 1 4 1 2
4 2 4 1 2 1
2 3 1 3 1 2
3 2 3 1 2 1
1 дорожка
2 доржка
3доржка
4 дор.
Р е ш е н о п е р е б о р о м в а р и а н т о в

Пример Задачи Комбинаторики
При игре в кости бросаются две кости, и выпавшие очки складываются; сколько существует комбинаций, таких, что сумма очков на верхних гранях равна двенадцати?
Решение: Каждый возможный исход соответствует функции (аргумент функции — это номер кости, значение — очки на верхней грани). Очевидно, что лишь 6+6 даёт нам нужный результат 12. Таким образом существует лишь одна функция, ставящая в соответствие 1 число 6, и 2 число 6. Или, другими словами, существует всего одна комбинация, такая, что сумма очков на верхних гранях равна двенадцати.

Разделы Комбинаторики!

Перечислительная комбинаторика
Перечислительная комбинаторика (или исчисляющая комбинаторика) рассматривает задачи о перечислении или подсчёте количества различных конфигураций (например, перестановок) образуемых элементами конечных множеств, на которые могут накладываться определённые ограничения, такие как: различимость или неразличимость элементов, возможность повторения одинаковых элементов и т. п.
Количество конфигураций, образованных несколькими манипуляциями над множеством, подсчитывается согласно правиламсложения и умножения.
Типичным примером задач данного раздела является подсчёт количества перестановок. Другой пример — известная Задача о письмах.

Вероятностная комбинаторика!
Этот раздел отвечает на вопросы вида: какова вероятность присутствия определённого свойства у заданного множества.

Краткая историческая справка
Первые работы, в которых зарождались основные понятия теории вероятностей,
представляли собой попытки создания теории азартных игр (Кардано, Гюйгенс,
Паскаль, Ферма и другие в XVI—XVII вв.).
Следующий этап развития теории вероятностей связан с именем Якоба Бернулли
(1654—1705). Доказанная им теорема, получившая впоследствии название «Закона
больших чисел», была первым теоретическим обоснованием накопленных ранее
фактов.
Дальнейшими успехами теория вероятностей обязана Муавру, Лапласу, Гауссу,
Пуассону и др.
Новый, наиболее плодотворный период связан с именами П. Л. Чебышева
(1821—1894) и его учеников А.А.Маркова(1856—1922) и А. М.Ляпунова
(1857—1918). В этот период теория вероятностей становится стройной
математической наукой. Ее последующее развитие обязано в первую очередь
русским и советским математикам (С. Н. Бернштейн, В. И. Романовский, А. Н.
Колмогоров, А. Я. Хинчин, Б. В. Гнеденко, Н. В. Смирнов и др.). В настоящее
время ведущая роль в создании новых ветвей теории вероятностей также
принадлежит советским математикам.

ЛИТЕРАТУРА
1. В.Ф.Бутузов, Ю.М.Колягин, Г.Л. Луканкин, Э.Г.Позняк и др. «Математика» учебное пособие для 11кл общеобразовательных учреждений /рекомендовано Министерством образования РФ/ М., Просвещение, 1996.
2. Е.А. Бунимович, В.А. Булычёв: «Вероятность и статистика», пособие для общеобразовательных учебных заведений 5 – 9 классы / допущено Министерством образования Российской Федерации // Дрофа Москва 2002
3. Н.Я. Виленкин, Р.С. Гутер, С.И. Шварцбурд, Б.В. Овчинский, В.Г. Ашкенузе:
«Алгебра» учебное пособие для IX – X классов средних школ с математической специализацией» / второе издание, «Просвещение», Москва 1972. 237 – 240)
4. Ю.Н. Макарычев, Н.Г.Миндюк «Алгебра: элементы статистики и теории вероятностей 7 – 9 классы» Под редакцией С.А.Теляковского М: Просвещение , 2006 г
5. Н.Я. Виленкин: «Индукция. Комбинаторика». Пособие для учителей. М., «Просвещение», 1976
6. В.Л. Лютикас: «Школьнику о теории вероятностей» Учебное пособие по факультативному курсу для учащихся 8 – 10 классов,/ М., «Просвещение» 1976
5.Журналы «Математика в школе»: № 10 – 2003 г, № 5 – 2004 г, № 6 – 2004 г, № 7 – 2004 г.
6. Математика 10-11 классы