Содержание
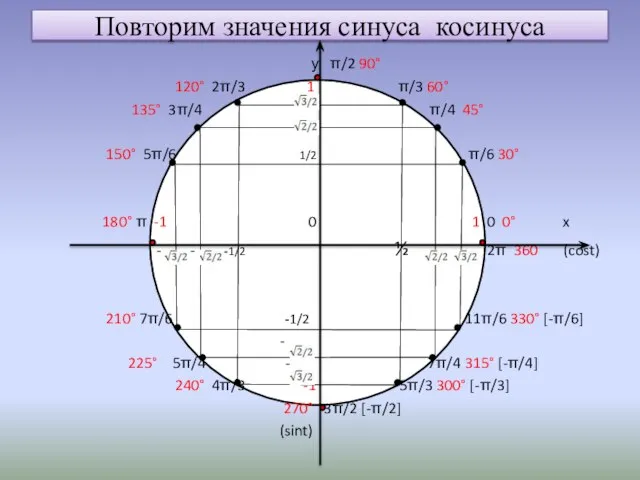
- 2. Повторим значения синуса косинуса у π/2 90° 120° 2π/3 1 π/3 60° 135° 3π/4 π/4 45°
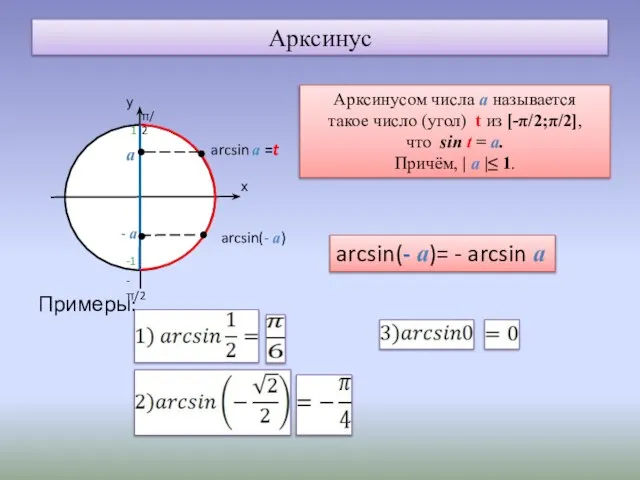
- 3. Арксинус Примеры: а - а arcsin(- а)= - arcsin а Арксинусом числа а называется такое число
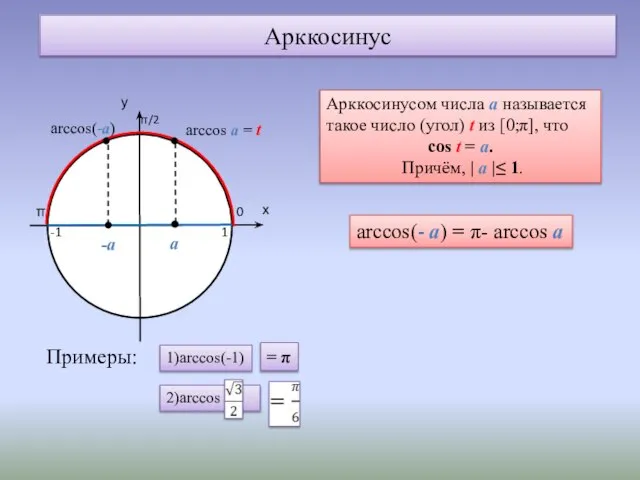
- 4. Арккосинус 0 π 1 -1 arccos(-а) Арккосинусом числа а называется такое число (угол) t из [0;π],
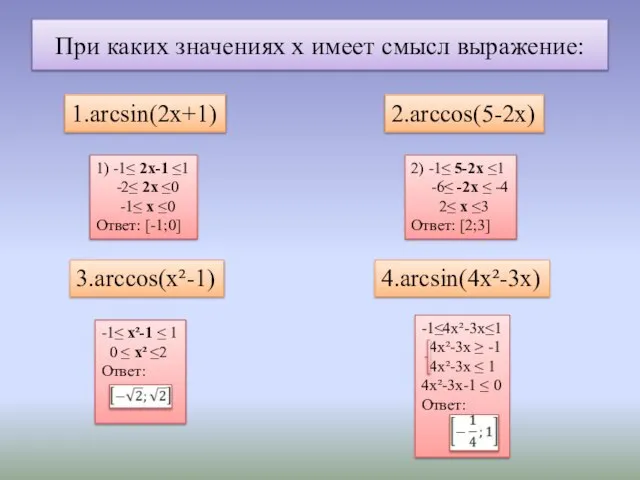
- 5. При каких значениях х имеет смысл выражение: 1.arcsin(2x+1) 2.arccos(5-2x) 3.arccos(x²-1) 4.arcsin(4x²-3x) 1) -1≤ 2х-1 ≤1 -2≤
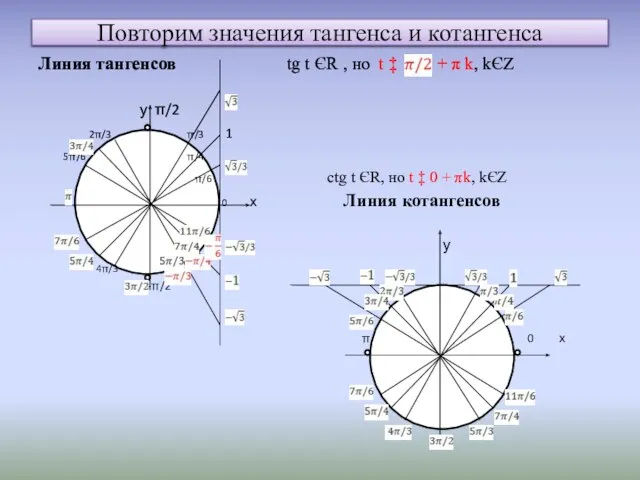
- 6. Повторим значения тангенса и котангенса Линия тангенсов tg t ЄR , но t ‡ + π
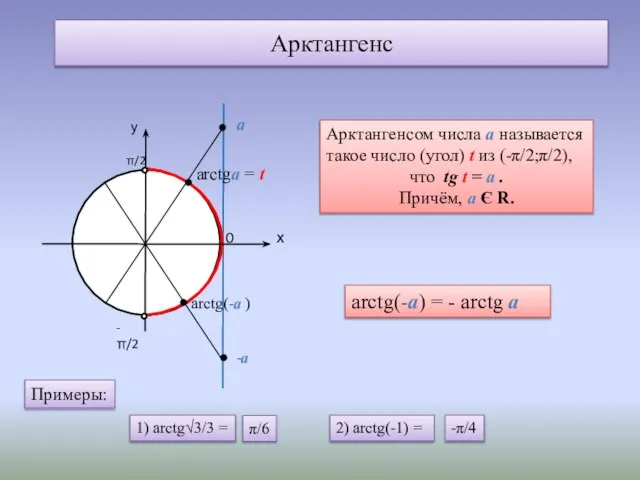
- 7. Арктангенс 0 arctgа = t Арктангенсом числа а называется такое число (угол) t из (-π/2;π/2), что
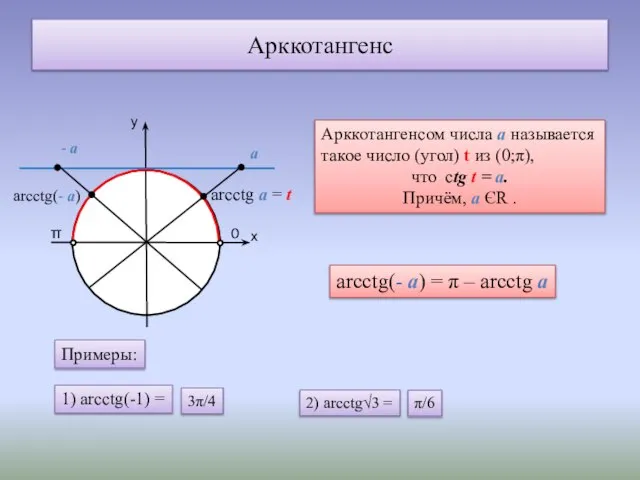
- 8. Арккотангенс у х 0 π arcctg а = t Арккотангенсом числа а называется такое число (угол)
- 9. Формулы корней простых тригонометрических уравнений 1.cost = а , где |а| ≤ 1 или Частные случаи
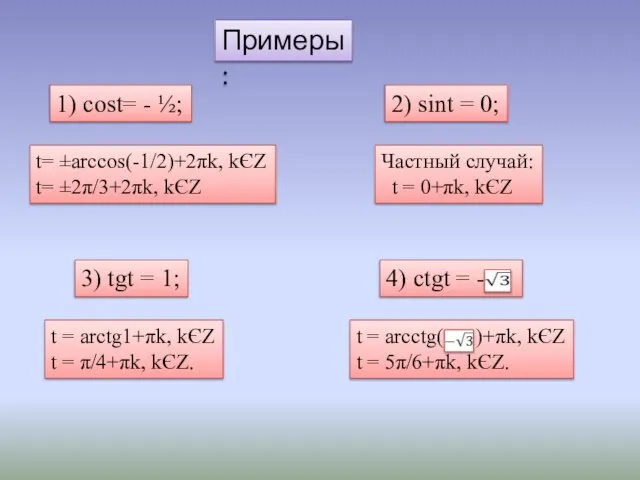
- 10. Примеры: 1) cost= - ½; 2) sint = 0; 3) tgt = 1; t= ±arccos(-1/2)+2πk, kЄZ
- 11. Решение простейших уравнений tg2x = -1 2x = arctg (-1) + πk, kЄZ 2x = -π/4
- 12. Другие тригонометрические уравнения 1.Сводимые к квадратным a∙sin²x + b∙sinx + c=0 Пусть sinx = p, где
- 14. Скачать презентацию



 Имущественные налоговые вычеты Подготовила: Клеутина Светлана ДС_01 __
Имущественные налоговые вычеты Подготовила: Клеутина Светлана ДС_01 __ Концептуальное искусство 1960-70 (е)
Концептуальное искусство 1960-70 (е) Экологические группы птиц 7 класс
Экологические группы птиц 7 класс самоменеджмент Занятие 1 (1)
самоменеджмент Занятие 1 (1) Эффективная презентация
Эффективная презентация ПРЯМОЙ МАРКЕТИНГ
ПРЯМОЙ МАРКЕТИНГ  Сложные слова. Образование сложных слов
Сложные слова. Образование сложных слов Жизнь_и_творчество_Петра_Андреевича_Вяземского
Жизнь_и_творчество_Петра_Андреевича_Вяземского Сотовая связь. От истоков до современности
Сотовая связь. От истоков до современности Золотые руки
Золотые руки Индивидуальная работа по дисциплине Проведение мониторинга на основе ГИС на тему Акустические системы
Индивидуальная работа по дисциплине Проведение мониторинга на основе ГИС на тему Акустические системы Огюст Конт (1798 – 1857)
Огюст Конт (1798 – 1857) Газета посвящается Последнему звонку
Газета посвящается Последнему звонку Анкета Отношение к классному руководителю
Анкета Отношение к классному руководителю Потребление воды и минеральных ресурсов
Потребление воды и минеральных ресурсов Упражнение утренней гимнастики
Упражнение утренней гимнастики ИСТОРИЯ ГОСУДАРСТВА И ПРАВА ДРЕВНЕГО РИМА
ИСТОРИЯ ГОСУДАРСТВА И ПРАВА ДРЕВНЕГО РИМА Презентация на тему Защита и резервирование информации
Презентация на тему Защита и резервирование информации  Информатизация образования в МОУ СОШ №2
Информатизация образования в МОУ СОШ №2 Право на защиту: тюрьма
Право на защиту: тюрьма Машиноведение. (5 класс)
Машиноведение. (5 класс) ИСТОРИЯ Часть 1
ИСТОРИЯ Часть 1 Обитатели морей и океанов. Фотоальбом
Обитатели морей и океанов. Фотоальбом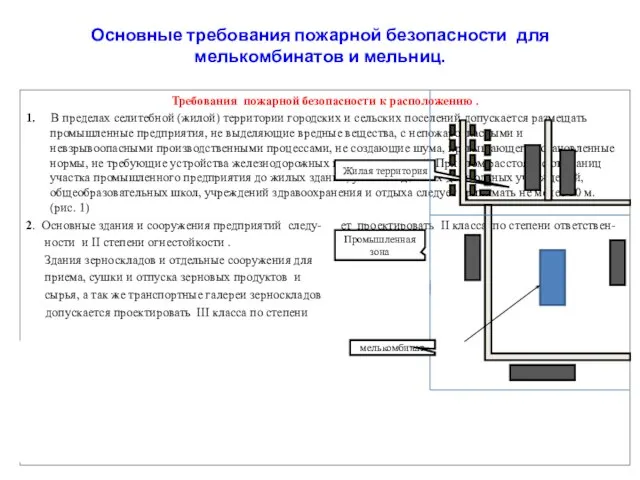 Основные требования пожарной безопасности для мелькомбинатов и мельниц.
Основные требования пожарной безопасности для мелькомбинатов и мельниц. Подготовка и проведение лыжных походов
Подготовка и проведение лыжных походов Урок по теме «Инерция» 7 класс
Урок по теме «Инерция» 7 класс Переливание крови
Переливание крови О внедрении курса «Основы религиозных культур и светской этики» (По материалам лекций курса «Духовно-нравственная культура в ус
О внедрении курса «Основы религиозных культур и светской этики» (По материалам лекций курса «Духовно-нравственная культура в ус