Содержание
- 2. Трудности теории Бора В теории Бора сохранились представления об орбитальном движении электронов в кулоновском поле ядра.
- 3. Трудности теории Бора В теории Бора сохранились представления об орбитальном движении электронов в кулоновском поле ядра.
- 4. Луи-де- Бройль
- 5. Электрон Фотон
- 6. В стационарном квантовом состоянии атома водорода на длине орбиты должно укладываться по идее де Бройля целое
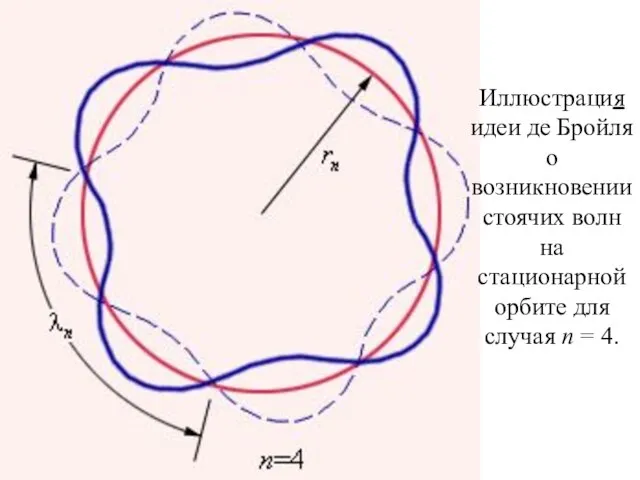
- 7. Иллюстрация идеи де Бройля о возникновении стоячих волн на стационарной орбите для случая n = 4.
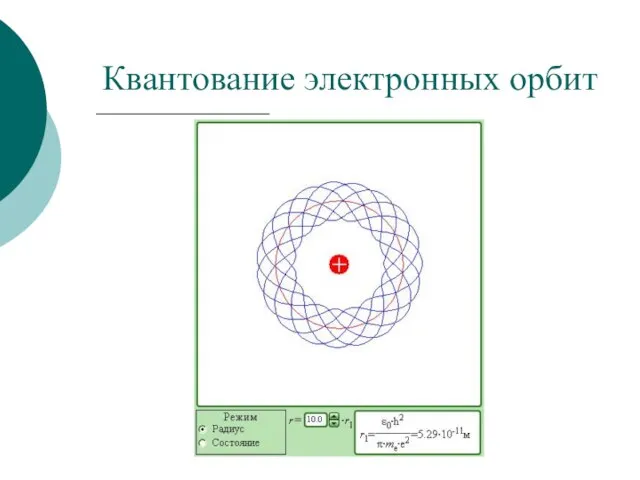
- 8. Квантование электронных орбит
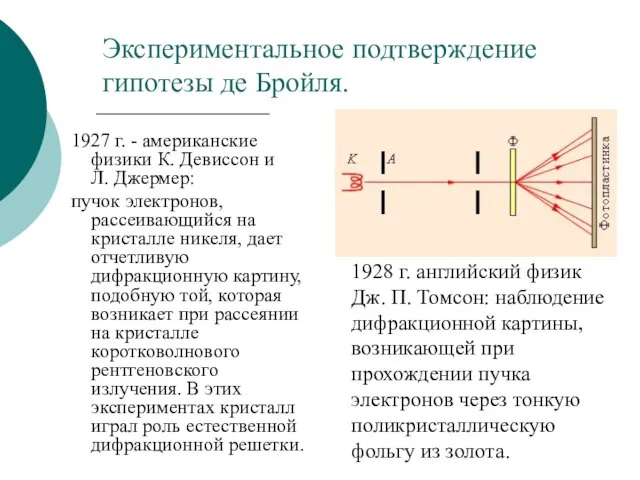
- 9. Экспериментальное подтверждение гипотезы де Бройля. 1927 г. - американские физики К. Девиссон и Л. Джермер: пучок
- 10. Дифракция электронов Картина дифракции электронов на поликристаллическом образце при длительной экспозиции (a) и при короткой экспозиции
- 11. Опыты Фабриканта, Бибермана, Сушкина Опыт Дж. Томсона был многократно повторен с неизменным результатом, в том числе
- 12. Волновые свойства макроскопических тел. Впоследствии дифракционные явления были обнаружены также для нейтронов, протонов, атомных и молекулярных
- 13. Квантовая механика Гипотеза де Бройля основывалась на соображениях симметрии свойств материи и не имела в то
- 14. Нильс Бор Принцип дополнительности Интерпретация квантовой механики
- 15. Принцип дополнительности Н.Бора Всем микрообъектам присущи и волновые, и корпускулярные свойства, однако, они не являются ни
- 16. Вернер Гейзенберг Матричная механика Соотношение неопределенностей
- 17. Соотношение неопределенностей В.Гейзенберга Микрочастицы в принципе не имеют одновременно точного значения координаты и соответствующей проекции импульса.
- 18. Эрвин Шредингер Волновая механика Волновое уравнение электрона – уравнение Шредингера
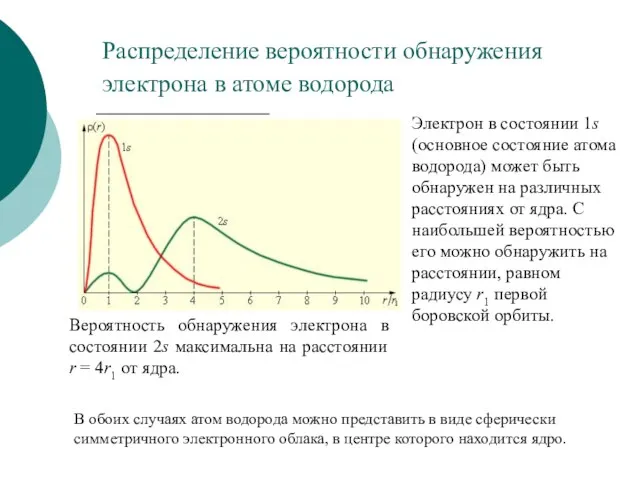
- 19. Распределение вероятности обнаружения электрона в атоме водорода В обоих случаях атом водорода можно представить в виде
- 20. Макс Борн Статистическая интерпретация волнового уравнения Доказательство идентичности волновой и матричной механики
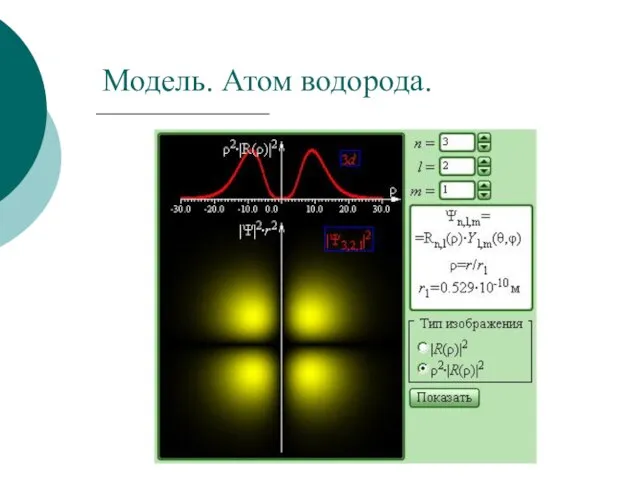
- 21. Модель. Атом водорода.
- 22. Доказательство связи квантовой и классической механики (наличие предельного перехода) Пауль Эренфест
- 24. Скачать презентацию


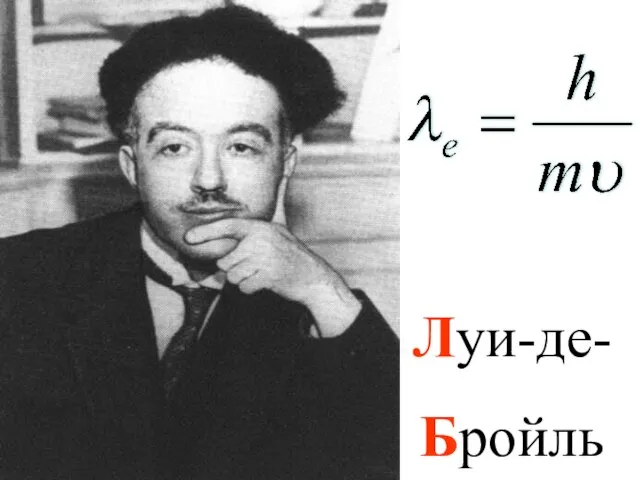













 Презентация на тему Вода - главный источник жизни
Презентация на тему Вода - главный источник жизни Презентация на тему Великие русские писатели
Презентация на тему Великие русские писатели  Использование игровых технологий на уроках географии
Использование игровых технологий на уроках географии Использование инновационных форм компьютерных технологий в обучении иностранному языку
Использование инновационных форм компьютерных технологий в обучении иностранному языку Основные понятия и определения изучаемые в разделе акробатика с элементами гимнастики
Основные понятия и определения изучаемые в разделе акробатика с элементами гимнастики Ostrov_mechty
Ostrov_mechty Физико - математические науки
Физико - математические науки Справится ли местоимение с ролью обращения?
Справится ли местоимение с ролью обращения? Современное и эффективное средство продвижения вашего продукта. Впервые на рынке Украины!
Современное и эффективное средство продвижения вашего продукта. Впервые на рынке Украины! Применение современных моделей автоматизации в профессиональной деятельности повара, кондитера
Применение современных моделей автоматизации в профессиональной деятельности повара, кондитера Крылатые крыловские слова
Крылатые крыловские слова Предупредим конфликт интересов. Викторина
Предупредим конфликт интересов. Викторина 70 лет снятия блокады Ленинграда
70 лет снятия блокады Ленинграда Культура Древнего Египта
Культура Древнего Египта  Свадебный рушник. Семейная реликвия семьи Коньшина Данила
Свадебный рушник. Семейная реликвия семьи Коньшина Данила TeleBingo new таблица
TeleBingo new таблица Программа фундаментальных исследований Президиума РАН № 27 «ОСНОВЫ ФУНДАМЕНТАЛЬНЫХ ИССЛЕДОВАНИЙ НАНОТЕХНОЛОГИЙ И НАНОМАТЕРИАЛО
Программа фундаментальных исследований Президиума РАН № 27 «ОСНОВЫ ФУНДАМЕНТАЛЬНЫХ ИССЛЕДОВАНИЙ НАНОТЕХНОЛОГИЙ И НАНОМАТЕРИАЛО Восточный базар
Восточный базар Презентация на тему Освоение Земли человеком (7 класс)
Презентация на тему Освоение Земли человеком (7 класс) Презентация на тему Второй и третий признаки подобия треугольников
Презентация на тему Второй и третий признаки подобия треугольников  Основы военной подготовки
Основы военной подготовки Презентация
Презентация Презентация на тему Технология обработки текстовой информации
Презентация на тему Технология обработки текстовой информации Манна
Манна 200-летию Победы России в Отечественной войне 1812 года посвящается
200-летию Победы России в Отечественной войне 1812 года посвящается Микрогибридные аккумуляторные технологии
Микрогибридные аккумуляторные технологии Социально-экономическое развитие пореформенной России в условиях экономического спада
Социально-экономическое развитие пореформенной России в условиях экономического спада Москва многонациональная
Москва многонациональная