Содержание
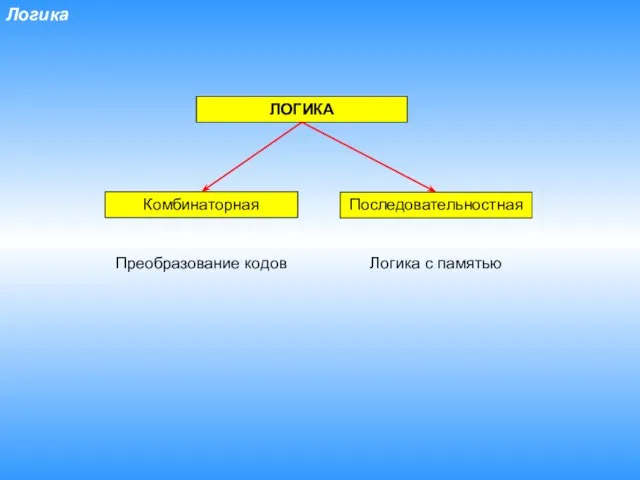
- 2. Логика ЛОГИКА Комбинаторная Последовательностная Преобразование кодов Логика с памятью
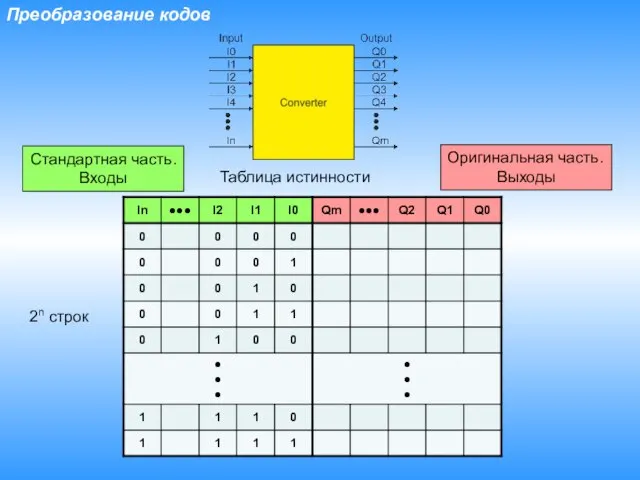
- 3. Преобразование кодов Таблица истинности Оригинальная часть. Выходы Стандартная часть. Входы 2n строк
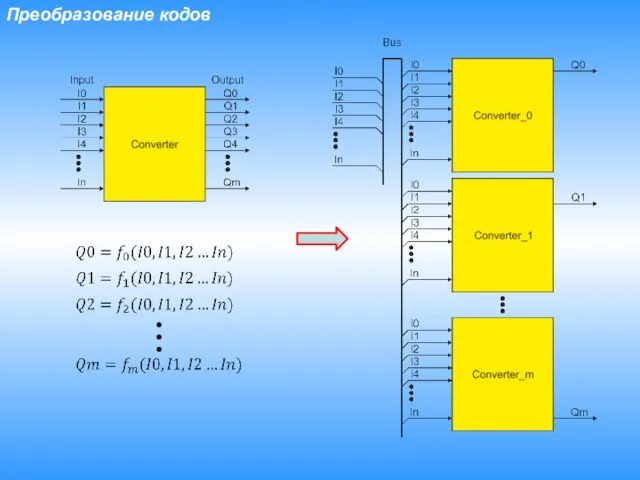
- 4. Преобразование кодов
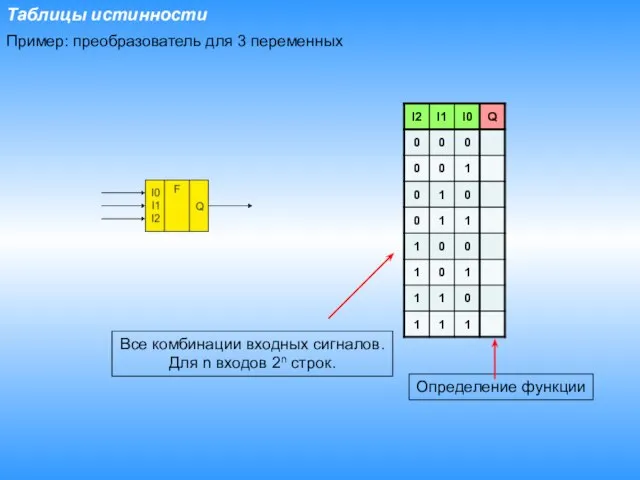
- 5. Таблицы истинности Все комбинации входных сигналов. Для n входов 2n строк. Определение функции Пример: преобразователь для
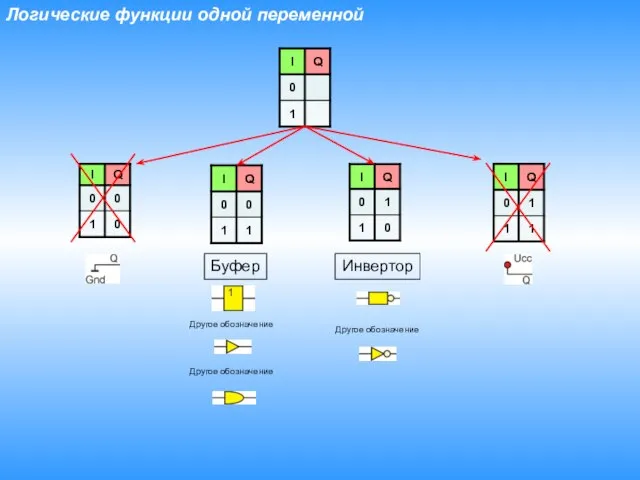
- 6. Функции одной переменной Рисунок из книги
- 7. Логические функции одной переменной Буфер Инвертор Другое обозначение Другое обозначение Другое обозначение
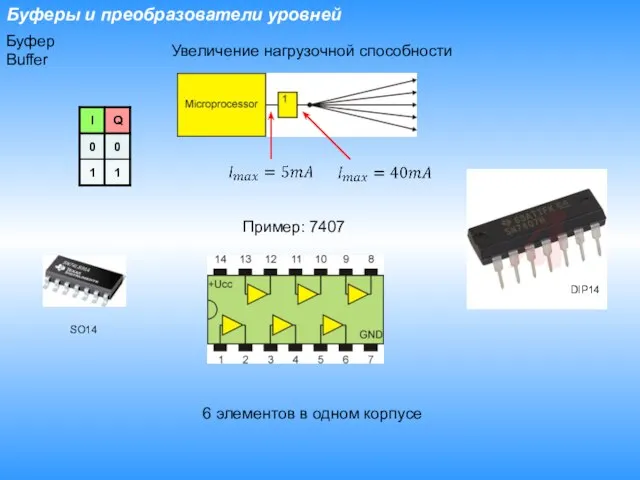
- 8. Буферы и преобразователи уровней Буфер Buffer Увеличение нагрузочной способности Пример: 7407 6 элементов в одном корпусе
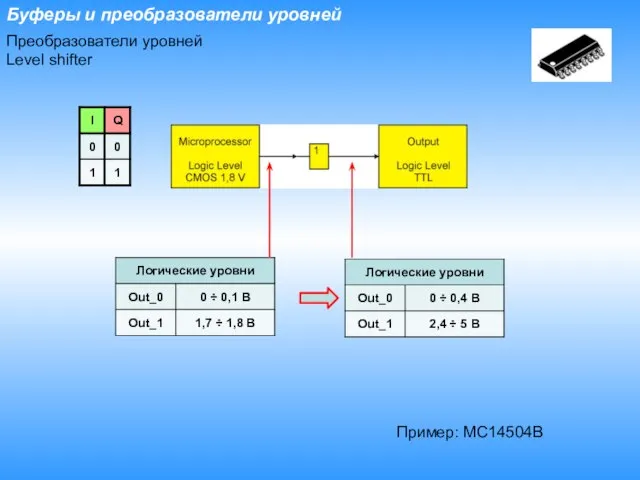
- 9. Буферы и преобразователи уровней Преобразователи уровней Level shifter Пример: MC14504B
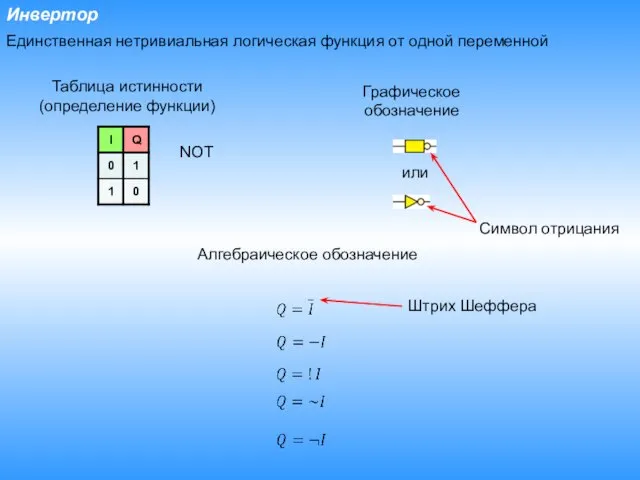
- 10. Инвертор Единственная нетривиальная логическая функция от одной переменной или Таблица истинности (определение функции) Графическое обозначение Символ
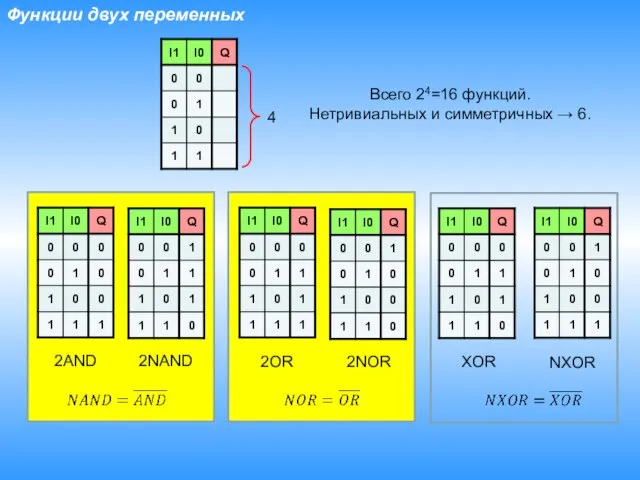
- 11. Функции двух переменных Всего 24=16 функций. Нетривиальных и симметричных → 6. 2AND 2NAND 2OR 2NOR XOR
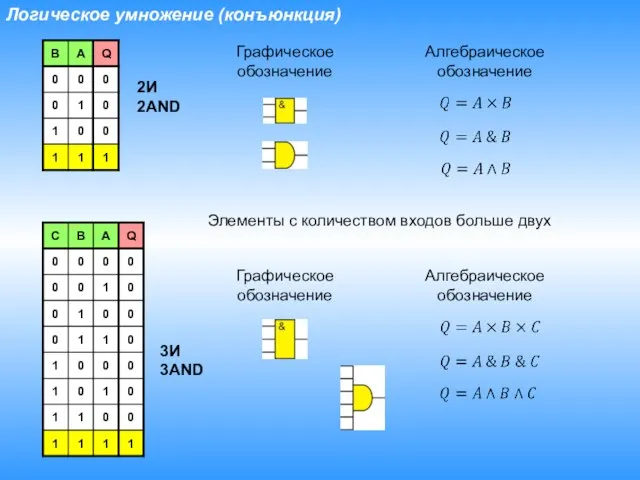
- 12. Логическое умножение (конъюнкция) Графическое обозначение Алгебраическое обозначение Элементы с количеством входов больше двух Графическое обозначение Алгебраическое
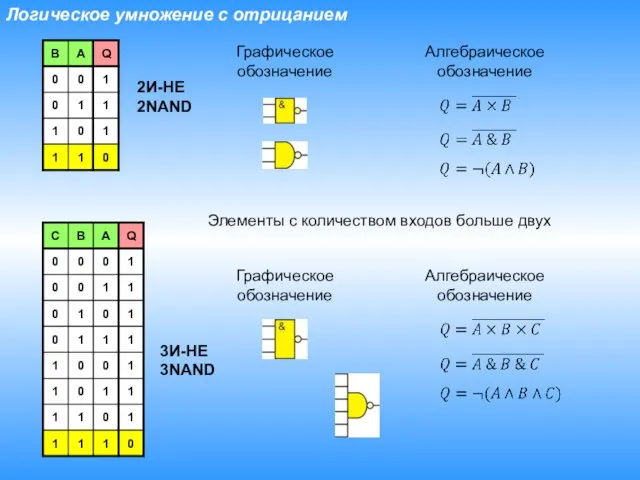
- 13. Логическое умножение с отрицанием Графическое обозначение Алгебраическое обозначение Элементы с количеством входов больше двух Графическое обозначение
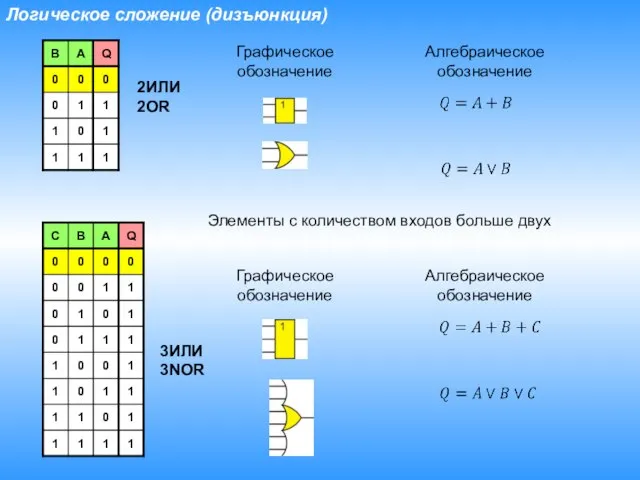
- 14. Логическое сложение (дизъюнкция) Графическое обозначение Алгебраическое обозначение Элементы с количеством входов больше двух Графическое обозначение Алгебраическое
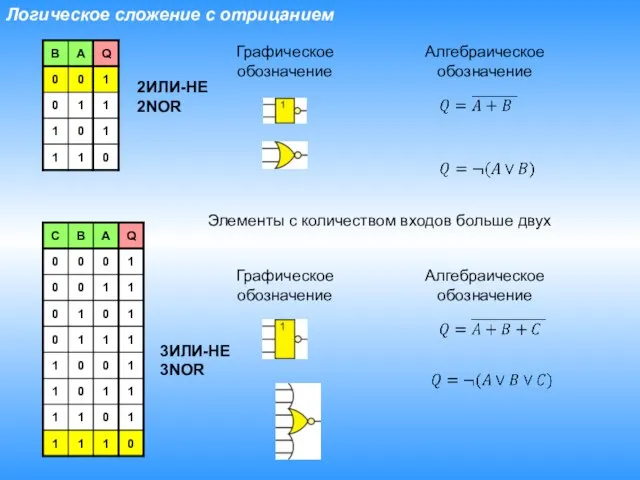
- 15. Логическое сложение с отрицанием Графическое обозначение Алгебраическое обозначение Элементы с количеством входов больше двух Графическое обозначение
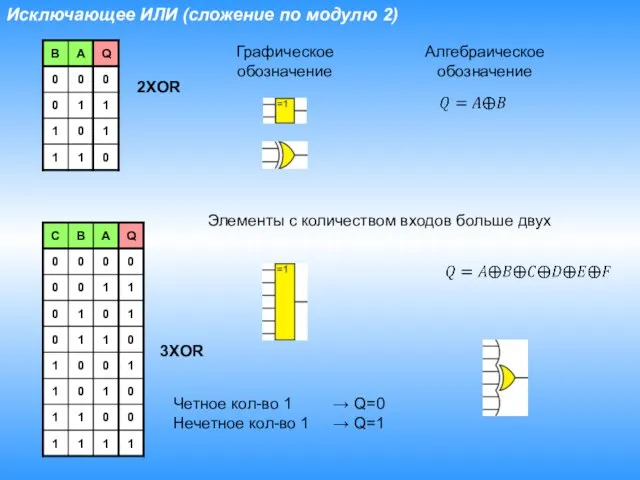
- 16. Исключающее ИЛИ (сложение по модулю 2) Графическое обозначение Алгебраическое обозначение Элементы с количеством входов больше двух
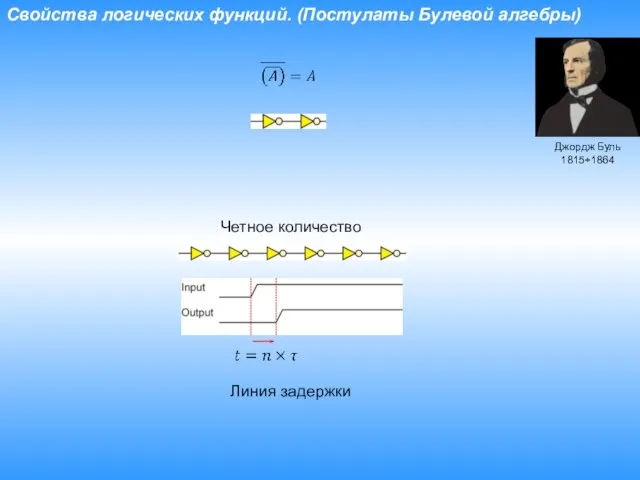
- 17. Свойства логических функций. (Постулаты Булевой алгебры) Джордж Буль 1815÷1864 Четное количество Линия задержки
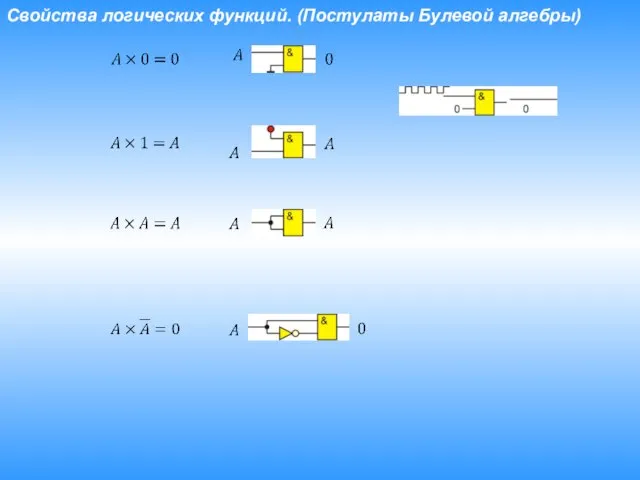
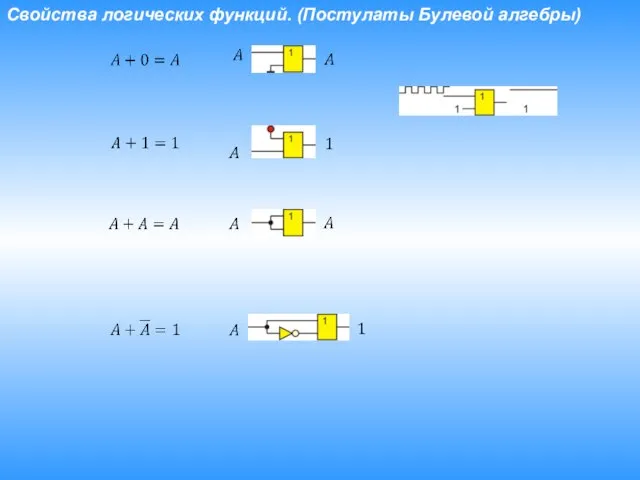
- 18. Свойства логических функций. (Постулаты Булевой алгебры)
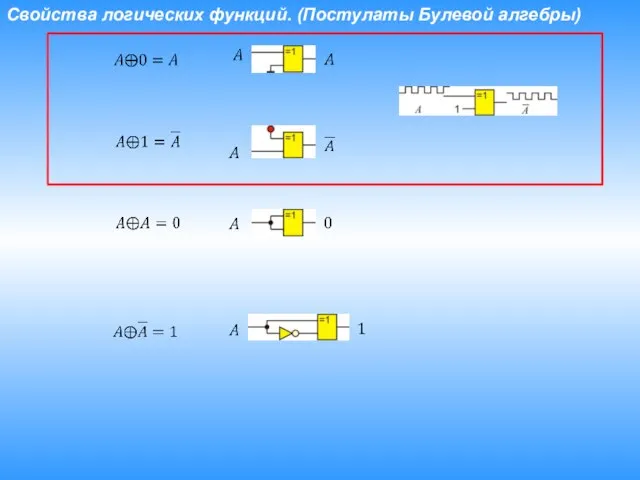
- 19. Свойства логических функций. (Постулаты Булевой алгебры)
- 20. Свойства логических функций. (Постулаты Булевой алгебры)
- 21. Законы Булевой алгебры Коммутативный
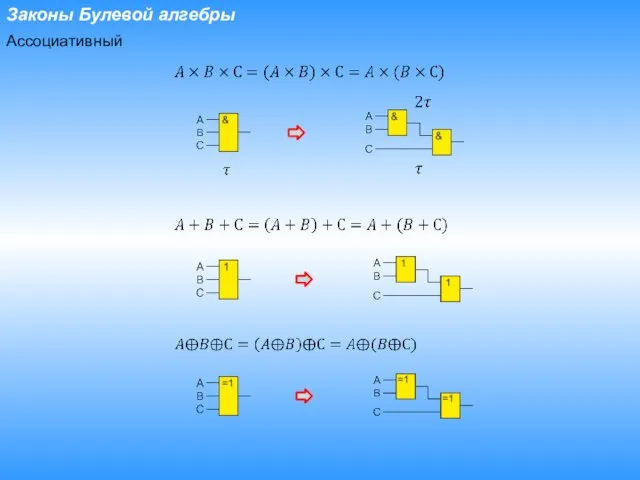
- 22. Законы Булевой алгебры Ассоциативный
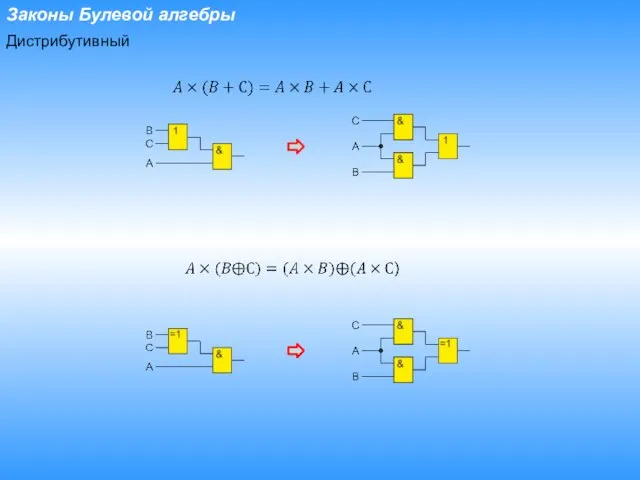
- 23. Законы Булевой алгебры Дистрибутивный
- 24. Свойства логических функций. (Постулаты Булевой алгебры) Поглощение
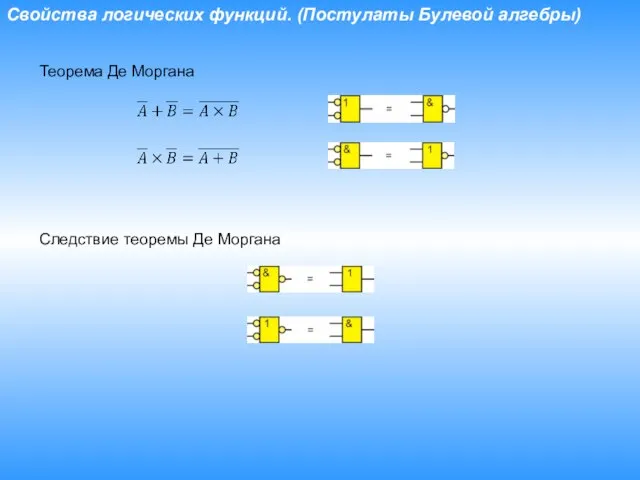
- 25. Свойства логических функций. (Постулаты Булевой алгебры) Теорема Де Моргана Следствие теоремы Де Моргана
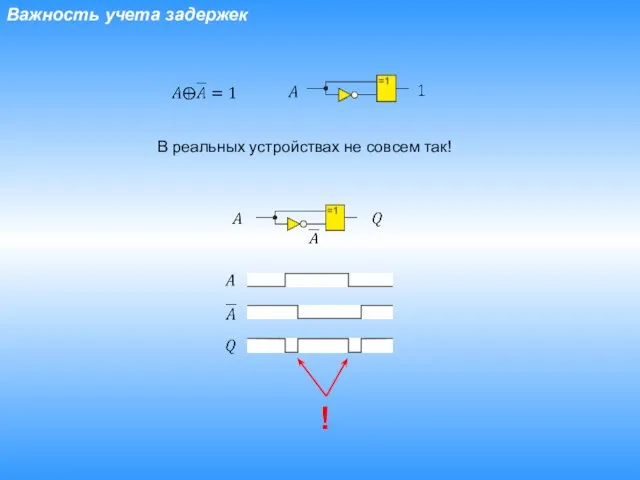
- 26. Важность учета задержек В реальных устройствах не совсем так! !
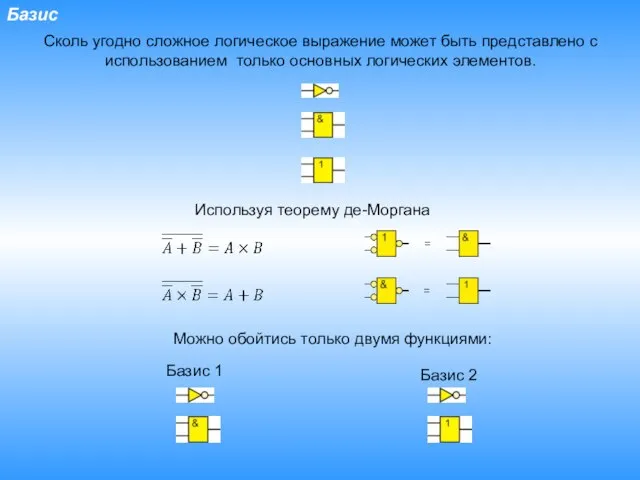
- 27. Базис Сколь угодно сложное логическое выражение может быть представлено с использованием только основных логических элементов. Используя
- 29. Скачать презентацию



 Презентация Microsoft PowerPoint
Презентация Microsoft PowerPoint Система стратегического планирования ООО «Сименс Россия»
Система стратегического планирования ООО «Сименс Россия» Презентация на тему Общая хирургическая инфекция
Презентация на тему Общая хирургическая инфекция  10 класс
10 класс Современные технологии и материалы
Современные технологии и материалы Почему нельзя жить без математики?
Почему нельзя жить без математики? Система Производственного менеджмента (СПМ)
Система Производственного менеджмента (СПМ) Моделирование из бумаги
Моделирование из бумаги Молочные и молокосодержащие продукты
Молочные и молокосодержащие продукты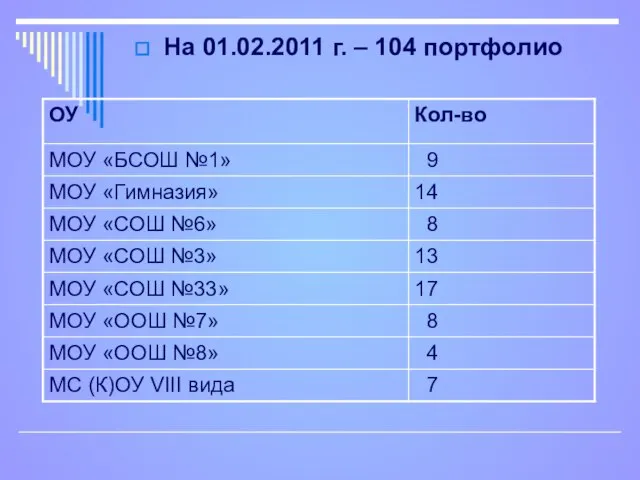 На 01.02.2011 г. – 104 портфолио
На 01.02.2011 г. – 104 портфолио Лихтенштейн
Лихтенштейн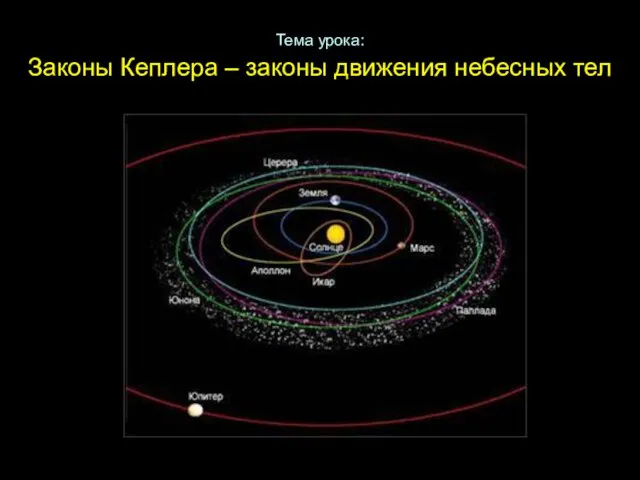 Тема урока: Законы Кеплера – законы движения небесных тел
Тема урока: Законы Кеплера – законы движения небесных тел Национальное пробуждение
Национальное пробуждение Мой класс и моя школа
Мой класс и моя школа Международный терроризм
Международный терроризм Культурные нормы. Мир человека
Культурные нормы. Мир человека Тела и вещества
Тела и вещества Юный разработчик. Занятие №9. Сборка. Динозавр
Юный разработчик. Занятие №9. Сборка. Динозавр Каталог Орифлейм. Акции
Каталог Орифлейм. Акции Моя семья Автор: Селиверстова Юлия, ученица 4-в класса
Моя семья Автор: Селиверстова Юлия, ученица 4-в класса «ПРАВА РЕБЁНКА»
«ПРАВА РЕБЁНКА» Media of the Usa
Media of the Usa Свойства льняных и хлопчатых тканей
Свойства льняных и хлопчатых тканей Рисуем трамвай
Рисуем трамвай Фарфор и керамика
Фарфор и керамика Солярис
Солярис Безопасность на транспорте
Безопасность на транспорте Атом мирный и военный
Атом мирный и военный