Удивительный мир симметрии

"Симметрия является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство.”
(Г. Вейль)
Г. Ессентуки Источник минеральной воды
Ватикан Площадь Святого Петра

Симметрия в природе – следствие необходимости сохранять устойчивость. Симметрия лежит в основе законов сохранения. Можно сказать, что симметрия – это проявление стремления материи к надёжности и прочности.
Российский самолёт ТУ-154
Автомобиль Renault

Что же такое симметрия?
В древности слово «симметрия» употреблялось в значении «гармония», «красота».
Будем называть симметрией фигуры, любое преобразование, переводящее фигуру в себя, т.е. обеспечивающее ее самосовмещение.
Найденное в гробнице Тутанхомона нагрудное украшение со священными знаками должно было гарантировать фараону воскрешение.

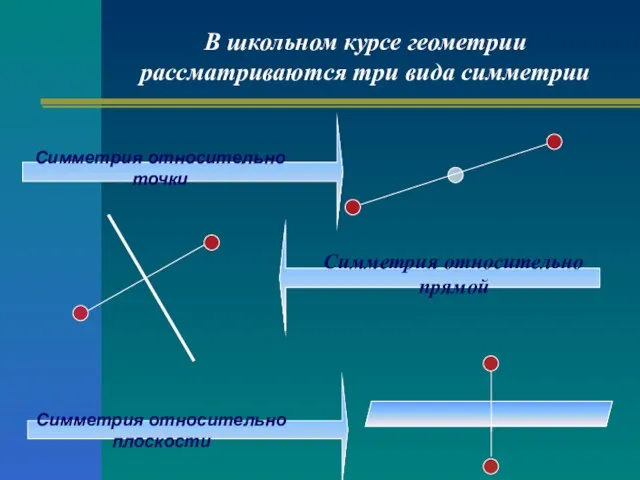
В школьном курсе геометрии рассматриваются три вида симметрии
Симметрия относительно прямой
Симметрия относительно точки
Симметрия относительно плоскости

Симметрия относительно точки
Фигура называется симметричной относительно точки, если для каждой точки фигуры симметричная ей точка также принадлежит этой фигуре.

Центральную симметрию можно встретить повсюду

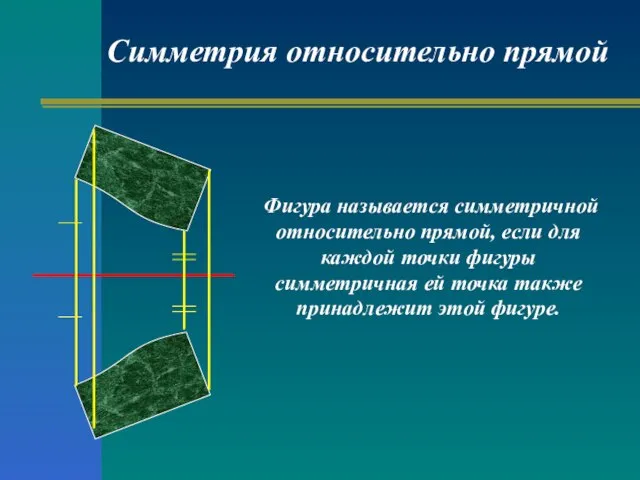
Фигура называется симметричной относительно прямой, если для каждой точки фигуры симметричная ей точка также принадлежит этой фигуре.
Симметрия относительно прямой

Осевая симметрия присутствует чуть ли не в каждом архитектурном объекте
Фрагмент чугунной решётки ворот Таврического дворца в Санкт-Петербурге
г.Ессентуки Грязелечебница
Германия Бонн Университет

Осевая симметрия в живой природе

Если преобразование симметрии относительно плоскости переводит фигуру в себя, то фигура называется симметричной относительно плоскости, а данная плоскость – плоскостью симметрии этой фигуры.
Симметрия относительно плоскости
β

Часто такую симметрию называют зеркальной. А зеркало не просто копирует объект, но и меняет местами передние и задние части объекта по отношению к зеркалу.
Дубаи Башни Эмиратов
Соловецкий монастырь
Германия Гамбург

Нетрадиционные виды симметрии
Винтовая симметрия
Симметрия поворота
Переносная симметрия

Винтовая симметрия

Переносная симметрия или скользящее преобразование

Симметрия поворота

Свойства симметрии
Симметрия многолика. Она обладает свойствами, которые одновременно и просты, и сложны, способны проявляться и единожды, и бесконечно много раз. Даже человек, мало знакомый с геометрией, легко выберет из предложенных ему фигур наиболее симметричные.

Симметрия треугольников
Равностороннй треугольник
Тождественное преобразование Е
Осевая симметрия S1,S2,S3
Повороты отн. О на 1200 и 2400
Разносторонний треугольник
Тождественное преобразование Е
Равнобедренный треугольник
Тождественное преобразование Е
Осевая симметрия S

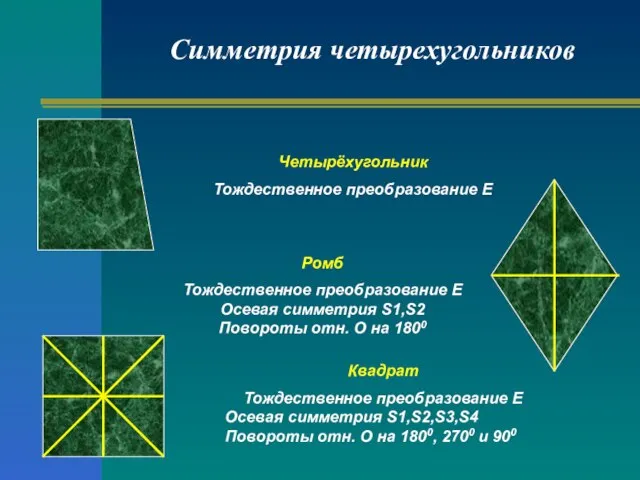
Симметрия четырехугольников
Четырёхугольник
Тождественное преобразование Е
Ромб
Тождественное преобразование Е
Осевая симметрия S1,S2
Повороты отн. О на 1800
Квадрат
Тождественное преобразование Е
Осевая симметрия S1,S2,S3,S4
Повороты отн. О на 1800, 2700 и 900

Круг и шар
Круг и шар – самые совершенные из фигур. Эти фигуры обладают бесконечным множеством симметрий.

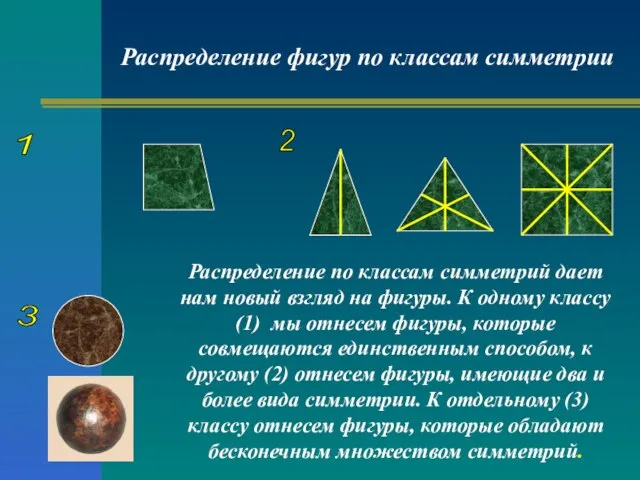
Распределение фигур по классам симметрии
Распределение по классам симметрий дает нам новый взгляд на фигуры. К одному классу (1) мы отнесем фигуры, которые совмещаются единственным способом, к другому (2) отнесем фигуры, имеющие два и более вида симметрии. К отдельному (3) классу отнесем фигуры, которые обладают бесконечным множеством симметрий.
1
2
3

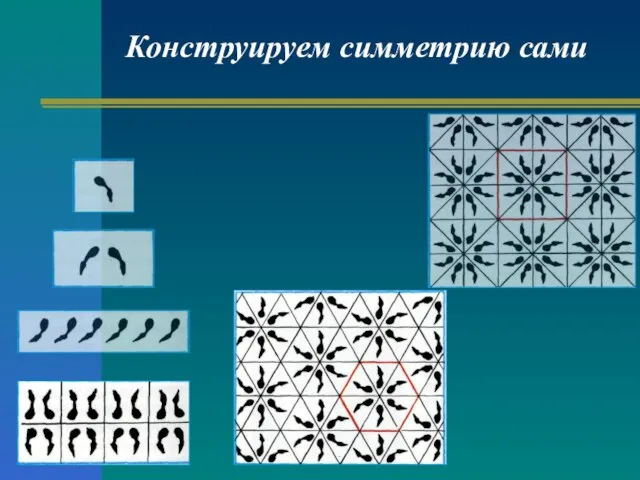
Конструируем симметрию сами

Симметрия танца

Симметрия и асимметрия
Симметрия и асимметрия - это две формы проявления одной и той же закономерности - закономерности двойственности.
Симметрия воспринимается нами как покой, скованность, закономерность, тогда как асимметрия означает движение, свободу, случайность.
Истинную красоту можно постичь только в единстве противоположностей
Москва Храм Христа Спасителя
Болгария София Александроневская лавра

Примером удивительного сочетания симметрии и асимметрии является Храм Василия Блаженного.
Это композиция из 10 храмов, каждый из которых обладает центральной симметрией, в целом асимметрична. Симметричные архитектурные детали собора как бы кружатся в асимметричном беспорядочном танце вокруг центрального шатра.

Природа – наука – искусство
Итак, сфера влияния симметрии поистине безгранична. Природа – наука – искусство, всюду мы видим противоборство, а часто и единство двух великих начал – симметрии и асимметрии, которые во многом и определяют гармонию природы, мудрость науки и красоту искусства.
Замок Белая цапля Япония
Канада Квебек Музей цивилизаций