Углы и отрезки, связанные с окружностью.

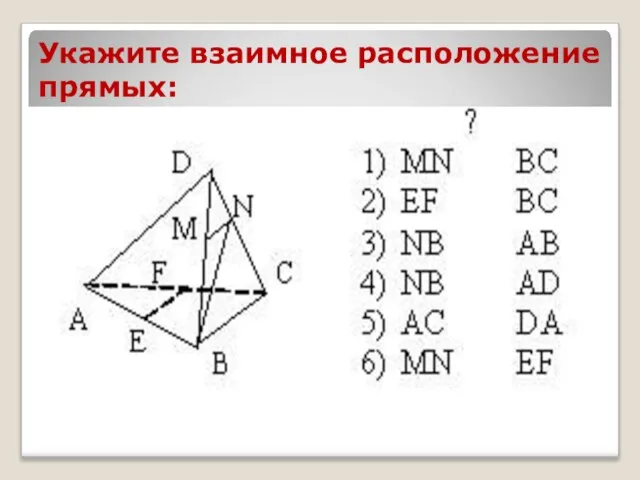
Укажите взаимное расположение прямых:

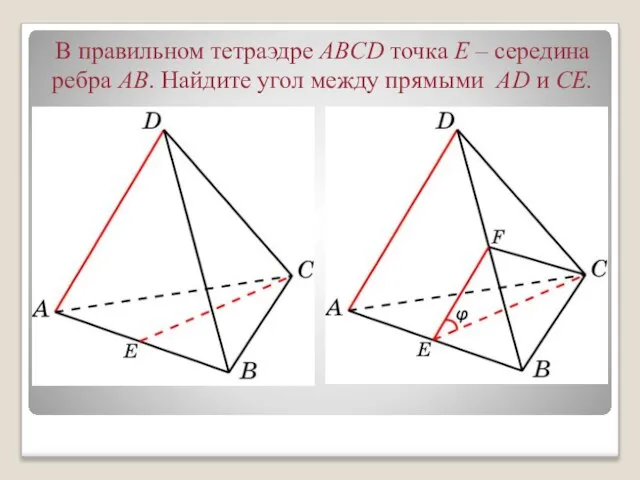
В правильном тетраэдре ABCD точка E – середина ребра AB. Найдите угол между прямыми AD и CE.

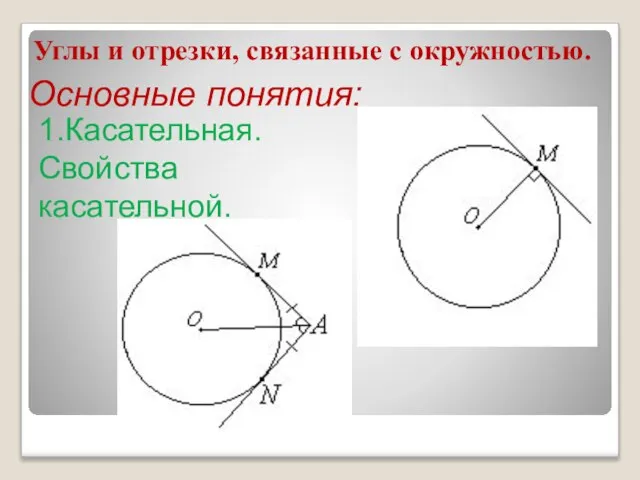
Углы и отрезки, связанные с окружностью.
Основные понятия:
1.Касательная. Свойства касательной.

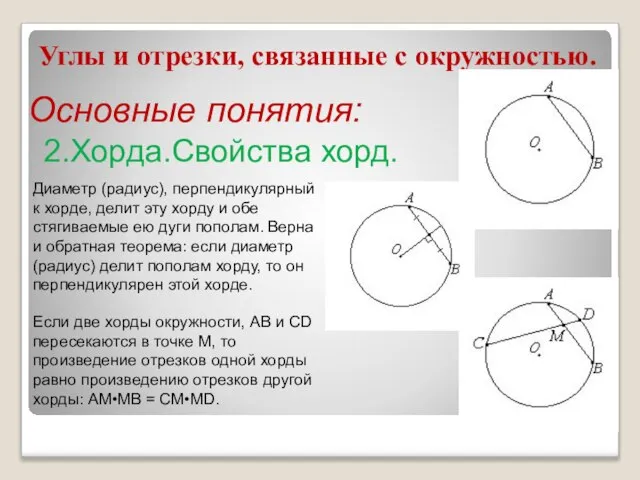
Углы и отрезки, связанные с окружностью.
Основные понятия:
2.Хорда.Свойства хорд.
Диаметр (радиус), перпендикулярный к хорде, делит эту хорду и обе стягиваемые ею дуги пополам. Верна и обратная теорема: если диаметр (радиус) делит пополам хорду, то он перпендикулярен этой хорде.
Если две хорды окружности, AB и CD пересекаются в точке M, то произведение отрезков одной хорды равно произведению отрезков другой хорды: AM•MB = CM•MD.

Свойства окружности:
Прямая может не иметь с окружностью общих точек; иметь с окружностью одну общую точку; иметь с ней две общие точки.
Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.
Точка касания двух окружностей лежит на линии, соединяющей
их центры.

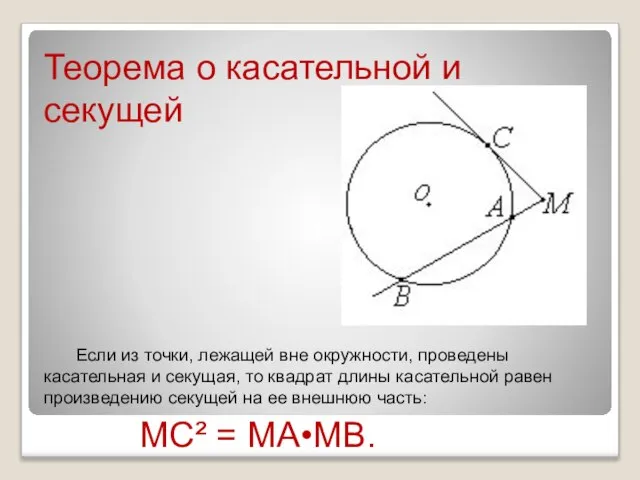
Теорема о касательной и секущей
Если из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на ее внешнюю часть:
MC² = MA•MB.