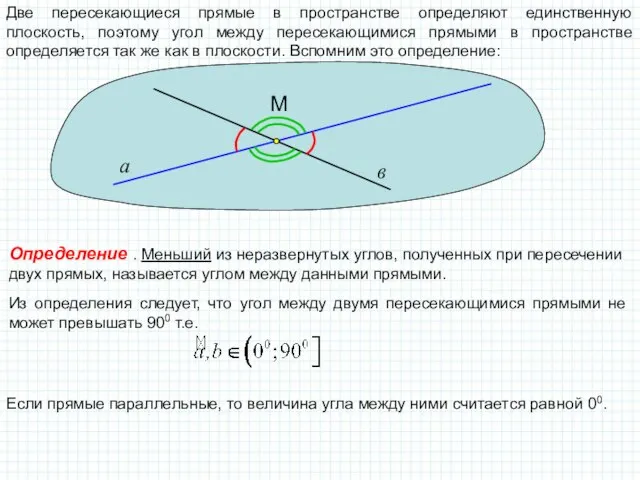
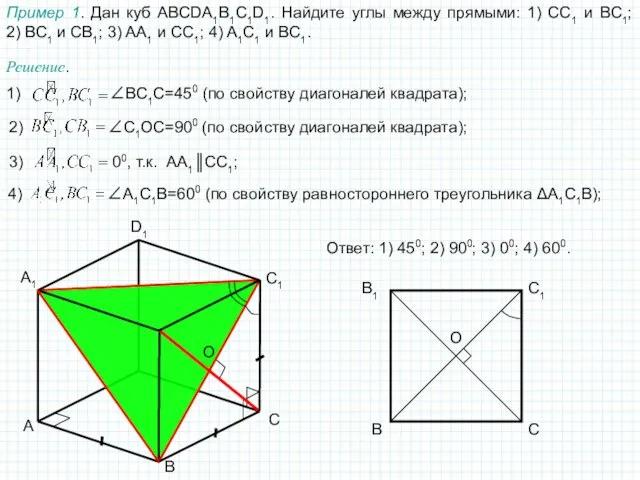
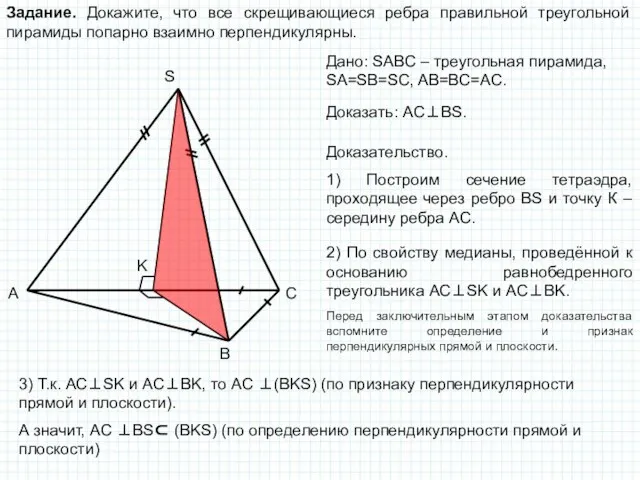
SABC – треугольная пирамида, SA=SB=SC, AB=BC=AC.
Доказать: AC⊥BS.
Доказательство.
1) Построим сечение тетраэдра, проходящее через ребро BS и точку К – середину ребра АС.
2) По свойству медианы, проведённой к основанию равнобедренного треугольника АС⊥SK и AC⊥BK.
3) Т.к. АС⊥SK и AC⊥BK, то АС ⊥(BKS) (по признаку перпендикулярности прямой и плоскости).
А значит, АС ⊥BS⊂ (BKS) (по определению перпендикулярности прямой и плоскости)
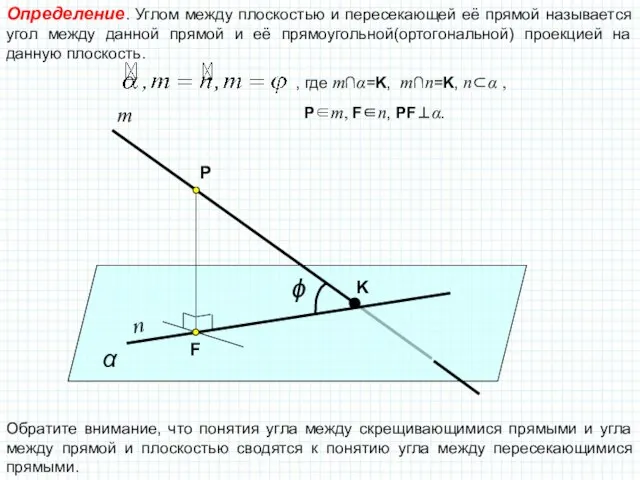
Перед заключительным этапом доказательства вспомните определение и признак перпендикулярных прямой и плоскости.


 Герой - кизеловец Алексей Щукин - сын полка
Герой - кизеловец Алексей Щукин - сын полка Знание научное и знание художественное
Знание научное и знание художественное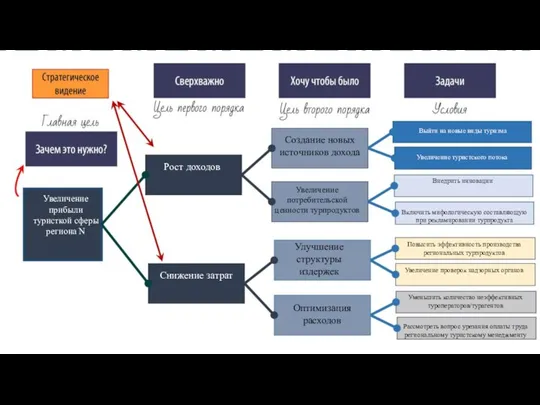 Дерево целей территории
Дерево целей территории Продюсерский центр «МОЙ ГОРОД»
Продюсерский центр «МОЙ ГОРОД» Люблю я Кавказ
Люблю я Кавказ Цели: Осознание актуальности реализации компетентностного подхода в школе;Создание условий к реализации компетентностного подх
Цели: Осознание актуальности реализации компетентностного подхода в школе;Создание условий к реализации компетентностного подх Роль системы воспитания и дополнительного образования учащихся в профилактике асоциальных явлений
Роль системы воспитания и дополнительного образования учащихся в профилактике асоциальных явлений Русская литература XIX века. А.С.Пушкин
Русская литература XIX века. А.С.Пушкин Презентация на тему Тренинги для развития навыка быстрого чтения для 3-4 классов
Презентация на тему Тренинги для развития навыка быстрого чтения для 3-4 классов  Оценка физического износа жилого здания в г. Нижний Новгород
Оценка физического износа жилого здания в г. Нижний Новгород Путешествие в неограниченную химию
Путешествие в неограниченную химию Занятия физкультурой и спортом
Занятия физкультурой и спортом Учет расходов на научно-исследовательские, опытно-конструкторские и технологические работы
Учет расходов на научно-исследовательские, опытно-конструкторские и технологические работы Оноре де Бальзак (1799 - 1850)
Оноре де Бальзак (1799 - 1850) Нежилое производственное здание (объект незавершенного строительства). Фото
Нежилое производственное здание (объект незавершенного строительства). Фото Современные принципы государственной политики в области МСБ: налоговое регулирование, доступ к финансам
Современные принципы государственной политики в области МСБ: налоговое регулирование, доступ к финансам MadameTussaud’s
MadameTussaud’s Примеры проблемных временных рядов и как работать с ними
Примеры проблемных временных рядов и как работать с ними Влияние психоэмоционального состояния и социальных условий жизни на здоровье подростка
Влияние психоэмоционального состояния и социальных условий жизни на здоровье подростка Для чего нужна пунктуация? ( урок- подготовка к сочинению – рассуждению на лингвистическую тему).
Для чего нужна пунктуация? ( урок- подготовка к сочинению – рассуждению на лингвистическую тему). Сочинение Решетников Опять двойка
Сочинение Решетников Опять двойка Формулировка проблемы. Материалы для подготовки к ЕГЭ
Формулировка проблемы. Материалы для подготовки к ЕГЭ Публичный доклад заведующей МДОУ «ЦРР-д/с №12» Галичиной Татьяны Викторовны
Публичный доклад заведующей МДОУ «ЦРР-д/с №12» Галичиной Татьяны Викторовны Численность и воспроизводство населения мира
Численность и воспроизводство населения мира Планирование как реализация свободы и проактивности
Планирование как реализация свободы и проактивности ОАО «КАМАЗ»
ОАО «КАМАЗ» Презентация на тему Республика Тыва
Презентация на тему Республика Тыва Нижегородская область
Нижегородская область