Содержание
- 2. Содержание: Для продолжения работы щелкните мышкой по соответствующей теме Понятие произведения целых неотрицательных чисел; Свойства умножения;
- 3. Умножение целых неотрицательных чисел Трем кроликам раздали по 4 морковки каждому. Сколько морковок раздали? Данное определение
- 4. Запишите это в тетрадь и щелкните мышкой по голубому полю экрана Для продолжения работы щелкните по
- 5. Запишите эти рассуждения. Чтобы проверить себя щелкните мышкой по второму примеру. Для продолжения работы щелкните мышкой
- 6. Свойства умножения Для действия сложения справедливы следующие свойства (законы): Свойство коммутативности (переместительный закон); Свойство ассоциативности (сочетательный
- 7. Свойства умножения (продолжение) Свойство коммутативности Для любых целых неотрицательных чисел а и b верно равенство: а
- 8. Запишите составленные Вами рассуждения. Для продолжения работы щелкните мышкой по управляющей кнопке. Сформулируйте эти правила. Чтобы
- 9. Задание: Закончите цепочку равенств, иллюстрирующую применение свойства ассоциативности в данном случае. Свойство ассоциативности (продолжение) Свойство ассоциативности
- 10. Свойства умножения (продолжение) Дистрибутивный закон умножения относительно сложения Для любых целых неотрицательных чисел а, b и
- 11. Дистрибутивный закон умножения (продолжение) Правило «Умножение суммы на число» используют для ознакомления с вычислительным приемом умножения
- 12. Выполните это задание. Для продолжения работы щелкните мышкой по голубому полю экрана. Свойства умножения (продолжение) Дистрибутивный
- 13. В выражении …, стоящем справа, первый множитель (не изменился, увеличился (уменьшился) в … раз(а)), второй множитель
- 14. Возврат в оглавление Изучение умножения в начальном курсе математики I этап. Ознакомление с умножением. На этом
- 15. Изучение умножения в НКМ (продолжение) Запишите это в тетрадь и щелкните мышкой по голубому полю экрана
- 16. Алгоритмы письменного умножения Алгоритм умножения многозначного числа на однозначное: Запишете второй множитель под разрядом единиц первого
- 17. Запишите это в тетрадь и щелкните мышкой по голубому полю экрана Алгоритм умножения многозначного числа на
- 19. Скачать презентацию
Слайд 2Содержание:
Для продолжения работы щелкните мышкой по соответствующей теме
Понятие произведения целых неотрицательных
Содержание:
Для продолжения работы щелкните мышкой по соответствующей теме
Понятие произведения целых неотрицательных
Свойства умножения;
Изучение умножения в начальном курсе математики.
Завершение работы
Множество No
Вычитание
Сложение
Деление
С помощью этих кнопок можно перейти в электронные конспекты по указанным темам.
Для возвращения в данный конспект нажмите
Слайд 3Умножение целых неотрицательных чисел
Трем кроликам раздали по 4 морковки каждому. Сколько морковок
Умножение целых неотрицательных чисел
Трем кроликам раздали по 4 морковки каждому. Сколько морковок

Данное определение соответствует представлению о числе как количественной характеристике множества, но не может являться основой методики изучения действия умножения в начальной школе. Смысл умножения дети усваивают, решая задачи на нахождение
Разбирая решение этой задачи, младшие школьники замечают, что все слагаемые данной суммы одинаковые, и учитель сообщает им, что решение этой задачи можно записать так:
Запишите это в тетрадь и щелкните мышкой по голубому полю экрана
Определение 11: Произведением целых неотрицательных чисел a и b называется целое неотрицательное число с, которое является численностью декартова произведения множества А на множество В, где n(A)=а; n(B)=b.
a ⋅ b = n(A х В)
Числа : a и b называются – множители, число с – произведение, запись a ⋅ b так же называется – произведение.
Определение 12: Действие, посредством которого находится произведение, называется умножением.
Для продолжения работы щелкните по управляющей кнопке.
Продолжите предложение, чтобы проверить себя щелкните мышкой по кнопке с вопросом. Для продолжения работы щелкните мышкой по голубому полю экрана.
4 + 4 + 4 = 12 (м)
4 ⋅ 3 = 12
Число 4 показывает, какое слагаемое складывали, а число 3 – сколько таких слагаемых взяли.
суммы одинаковых слагаемых. Например:
Слайд 4Запишите это в тетрадь и щелкните мышкой по голубому полю экрана
Для
Запишите это в тетрадь и щелкните мышкой по голубому полю экрана
Для

Умножение целых неотрицательных чисел (продолжение)
В данной задаче рассматриваются 3 равночисленных множества морковок:
n(A1) = n(A2) = n(A3) = 4.
A1
A2
A3
Решая задачу, дети находят
Продолжите предложение. Чтобы проверить себя щелкните мышкой по кнопке с вопросом. Для продолжения работы щелкните мышкой по голубому полю экрана.
численность объединения множеств
A1, А2, А3:
n (A1 ∪ А2 ∪ А3) = 4 ⋅ 3 = 12
Исходя из этого, понятие «произведение» можно определить так:
Определение 13: Произведением целых неотрицательных чисел a и b называется целое неотрицательное число с, которое является численностью объединения b непересекающихся множеств, численность каждого из которых равна a:
b множеств
По определению 13 нельзя найти произведение в особых случаях умножения:
умножение на 0;
умножение на 1, так как нельзя объединить 1 или 0 множеств.
Так как определение 13 рассматривает произведение как численность объединения равночисленных множеств, а объединение связано с действием , то понятие «произведение» можно определить через понятие .
Определение 14: Произведением целых неотрицательных чисел a и b называется целое неотрицательное число с, полученное по одному из следующих правил:
b слагаемых
Ответы в особых случаях находятся по данному определению.
, где n(A1) = n(A2) =…= n(Ab) = a.
a ⋅ b = n (A1 ∪ А2 ∪ А3 ∪ … ∪ Аb)
1. если b = 0, то a ⋅ b = a ⋅ 0 = 0; 2. если b = 1, то a ⋅ b = a ⋅ 1 = а;
3. если b > 1, то a ⋅ b = a + a + a + … + a
Продолжите предложение. Чтобы проверить себя щелкните мышкой по кнопкам с вопросом. При повторном щелчке подсказка исчезнет.
Для продолжения работы щелкните мышкой по голубому полю экрана.
сложение
«сумма»
Слайд 5Запишите эти рассуждения.
Чтобы проверить себя щелкните мышкой по второму примеру.
Для продолжения
Запишите эти рассуждения.
Чтобы проверить себя щелкните мышкой по второму примеру.
Для продолжения

Запишите это в тетрадь. Прочитайте выражение записанное символами.
Если Вы затрудняетесь это сделать щелкните мышкой по знаку вопроса.
В этом случае, советуем Вам записать, как читается это математическое предложение.
Для продолжения работы щелкните мышкой по голубому полю
Умножение целых неотрицательных чисел (продолжение)
Задание 1: 1. Найдите значения данных выражений, заменив суммой;
4 ⋅ 5
3 ⋅ 6
6 ⋅ 3
7 ⋅ 4
Выполните данное задание.
Для продолжения работы щелкните мышкой по голубому полю экрана.
Задание 2: Составьте задачу на нахождение суммы одинаковых слагаемых. Сделайте рисунок к этой задаче. Что означает каждое число в записи решения Вашей задачи?
Задание 4: Детям было предложено задание: «Составьте всевозможные двузначные числа из цифр 3, 5, 6, 9».
Сколько чисел смогут составить дети?
Какое определение произведения лежит в основе ответа на этот вопрос?
Задание 3: Сформулируйте задание на нахождение суммы одинаковых слагаемых, в котором в качестве наглядности использовался бы такой прямоугольник. Что означает каждое число в решении Вашего задания?
Для продолжения работы вернитесь в оглавление.
2. Запишите, что с точки зрения каждого определения произведения Вы нашли;
3. Сделайте рисунки, которые помогут детям найти эти произведения.
Задание 5: Как будут рассуждать дети, сравнивая выражения:
7 ⋅ 5 … 7 + 7 + 7 + 7
6 ⋅ 4 … 6 + 6 + 6 + 7
в выражении 6 ⋅ 4 число 6 повторили слагаемым 4 раза;
в выражении 6 + 6 + 6 + 7 тоже четыре слагаемых, но одно из них 7.
6 меньше 7, значит выражение 6 ⋅ 4 меньше выражения 6 + 6 + 6 + 7.
Для действия умножения справедлива теорема:
Теорема: Для любых целых неотрицательных чисел a и b существует и при том только одно целое неотрицательное число с, которое является произведением чисел a и b . (∀а,b∈No) ∃! с∈Nо: с = а ⋅ b
Запишите это в тетрадь и щелкните мышкой по голубому полю экрана
Для любых целых неотрицательных чисел a и b существует единственное целое неотрицательное число с, такое, что с = a ⋅ b
Слайд 6Свойства умножения
Для действия сложения справедливы следующие свойства (законы):
Свойство коммутативности (переместительный закон);
Свойства умножения
Для действия сложения справедливы следующие свойства (законы):
Свойство коммутативности (переместительный закон);

Дистрибутивные свойства (распределительные законы)
умножения относительно сложения,
умножения относительно вычитания;
Свойство монотонности.
Запишите это в тетрадь.
Для продолжения работы щелкните мышкой по выделенному свойству. После ознакомления щелкните мышкой по голубому полю экрана.
Задание: Для данных выражений :
7 ⋅ 4
43 ⋅ 2
13 ⋅ 20
47000 ⋅ 5
Для продолжения работы вернитесь в оглавление.
запишите развернутое решение и найдите значение;
опишите, что с точки зрения всех определений произведения Вы нашли;
определите какое свойство или свойства лежит в основе вычислительного приема;
придумайте задачу или задание, иллюстрирующие данное свойство запишите все способы решения данной задачи (задания), составлением числовых выражений.
Слайд 7Свойства умножения (продолжение)
Свойство коммутативности
Для любых целых неотрицательных чисел а и b верно
Свойства умножения (продолжение)
Свойство коммутативности
Для любых целых неотрицательных чисел а и b верно
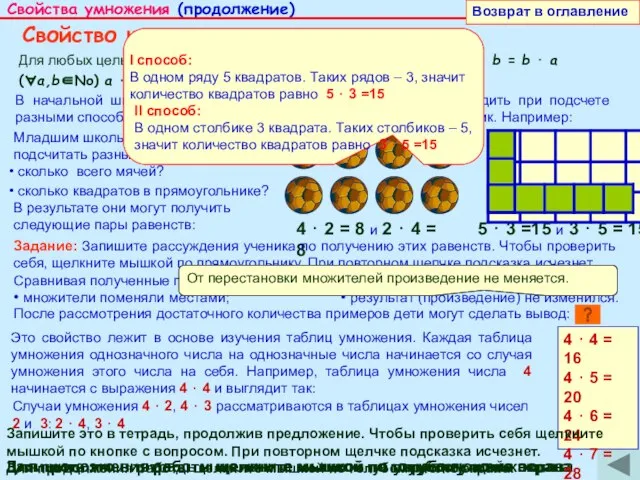
(∀а,b∈No) а ⋅ b = b ⋅ а
В начальной школе знакомство с данным свойством может проходить при подсчете разными способами количества предметов, образующих прямоугольник. Например:
Младшим школьникам предлагается подсчитать разными способами:
сколько всего мячей?
сколько квадратов в прямоугольнике?
В результате они могут получить следующие пары равенств:
Запишите это в тетрадь и щелкните мышкой по голубому полю экрана
4 ⋅ 2 = 8 и 2 ⋅ 4 = 8
Сравнивая полученные пары равенств дети замечают, что
множители поменяли местами;
результат (произведение) не изменился.
После рассмотрения достаточного количества примеров дети могут сделать вывод:
Задание: Запишите рассуждения ученика по получению этих равенств. Чтобы проверить себя, щелкните мышкой по прямоугольнику. При повторном щелчке подсказка исчезнет.
Для продолжения работы щелкните мышкой по управляющей кнопке.
Это свойство лежит в основе изучения таблиц умножения. Каждая таблица умножения однозначного числа на однозначные числа начинается со случая умножения этого числа на себя. Например, таблица умножения числа 4 начинается с выражения 4 ⋅ 4 и выглядит так:
5 ⋅ 3 =15 и 3 ⋅ 5 = 15
I способ:
В одном ряду 5 квадратов. Таких рядов – 3, значит количество квадратов равно 5 ⋅ 3 =15
II способ:
В одном столбике 3 квадрата. Таких столбиков – 5, значит количество квадратов равно 3 ⋅ 5 =15
Для продолжения работы щелкните мышкой по голубому полю экрана
4 ⋅ 4 = 16
4 ⋅ 5 = 20
4 ⋅ 6 = 24
4 ⋅ 7 = 28
4 ⋅ 8 = 32
4 ⋅ 9 = 36
Случаи умножения 4 ⋅ 2, 4 ⋅ 3 рассматриваются в таблицах умножения чисел 2 и 3: 2 ⋅ 4, 3 ⋅ 4
От перестановки множителей произведение не меняется.
Запишите это в тетрадь, продолжив предложение. Чтобы проверить себя щелкните мышкой по кнопке с вопросом. При повторном щелчке подсказка исчезнет.
Для продолжения работы щелкните мышкой по голубому полю экрана.
Слайд 8Запишите составленные Вами рассуждения.
Для продолжения работы щелкните мышкой по управляющей кнопке.
Сформулируйте
Запишите составленные Вами рассуждения.
Для продолжения работы щелкните мышкой по управляющей кнопке.
Сформулируйте

Чтобы проверить себя щелкните мышкой по голубому полю экрана
Запишите это в тетрадь и щелкните мышкой по голубому полю экрана
Это свойство можно заменить двумя правилами:
Чтобы умножить произведение на число
умножение произведения на число
умножение числа на произведение
можно умножить на это число 2-ой множитель и полученный результат умножить на 1-ый множитель
Чтобы умножить число на произведение
можно умножить это число на 2-ой множитель и полученный результат умножить на 1-ый множитель
можно умножить на это число 1-ый множитель и полученный результат умножить на 2-ой множитель
можно умножить это число на 1-ый множитель и полученный результат умножить на 2-ой множитель
I способ:
Сначала подсчитаем количество кубиков в одном горизонтальном слое:
в одном ряду 5 кубиков;
в одном слое 3 таких ряда, значит количество кубиков одном горизонтальном слое равно 5 ⋅ 3
Таких слоев у нас 2, следовательно всего кубиков (5 ⋅ 3) ⋅ 2 = 30
Свойства умножения (продолжение)
Свойство ассоциативности
Для любых целых неотрицательных чисел а, b и с верно равенство: (а ⋅ b) ⋅ с = а ⋅ (b ⋅ с)
(∀а,b,с ∈No) (а ⋅ b) ⋅ с = а ⋅ (b ⋅ с)
(a ⋅ b) ⋅ c
=(a ⋅ c) ⋅ b
=(b ⋅ c) ⋅ a
a ⋅ (b ⋅ c)
= (a ⋅ b) ⋅ c
= (a ⋅ c) ⋅ b
Для иллюстрации данного свойства можно различными способами подсчитать количество кубиков, составляющих прямоугольный параллелепипед.
Задание: Запишите способы рассуждения для получения различных равенств при подсчете кубиков в данном параллелепипеде: (5 ⋅ 3) ⋅ 2 = 30 (5 ⋅ 2) ⋅ 3 = 30
(3 ⋅ 2) ⋅ 5 = 30, иллюстрирующих свойство ассоциативности. Чтобы проверить себя и посмотреть один из способов, щелкните мышкой по вопросительному знаку.
Слайд 9Задание: Закончите цепочку равенств, иллюстрирующую применение свойства ассоциативности в данном случае.
Свойство ассоциативности
Задание: Закончите цепочку равенств, иллюстрирующую применение свойства ассоциативности в данном случае.
Свойство ассоциативности

Свойство ассоциативности и соответствующие ему правила в явном виде не изучаются в начальной школе, но на них основано изучение вычислительных приемов умножения круглых чисел. Например, при вычислении значения выражения 87000 ⋅ 4 дети могут рассуждать так: Чтобы 87000 умножить на 4 можно 87 умножить на 4 и полученный результат 348 умножить на 1000, т. е. приписать к числу 348 три нуля.
87000 ⋅ 4 = (87 ⋅ 1000) ⋅ 4 = (87 ⋅ 4) ⋅ 1000 = 348000
Этому рассуждению соответствует такая цепочка равенств:
Запишите это в тетрадь и щелкните мышкой по голубому полю экрана
Задания: 1. Какое правило лежит в основе данного рассуждения?
2. Запишите рассуждения ученика при решении примера 87 ⋅ 400.
Запишите соответствующую ему цепочку равенств. Какое правило применяется в этом случае?
Для продолжения щелкните мышкой по голубому полю экрана
Свойство ассоциативности лежит в основе алгоритма письменного умножения круглых чисел и правила записи этих чисел. Например, для вычисления значения выражения 8730 ⋅ 4200, дети его запишут столбиком так.
Выполняя вычисления, они 837 умножат на 42 и к полученному результату припишут столько нулей, сколько их было в 1-ом и 2-ом множителях вместе, то есть три нуля.
8730 ⋅ 4200 = (873 ⋅ 10) ⋅ 4200 = (873 ⋅ 4200) ⋅ 10 = (843 ⋅ (42 ⋅ 100)) ⋅ 10 = …
Для продолжения работы щелкните мышкой по управляющей кнопке.
Данное решение соответствует такой записи с использование свойства ассоциативности:
Слайд 10Свойства умножения (продолжение)
Дистрибутивный закон умножения относительно сложения
Для любых целых неотрицательных чисел а,
Свойства умножения (продолжение)
Дистрибутивный закон умножения относительно сложения
Для любых целых неотрицательных чисел а,

(а + b) ⋅ с = а ⋅ с + b ⋅ с
(∀а,b,с ∈No) (а + b) ⋅ с = а ⋅ с + b ⋅ с
Для знакомства с данным правилом можно предложить детям задачу, имеющую два способа решения. Числа в условии подбирают так, чтобы все вычисления проходили в пределах таблицы умножения.
В начальной школе знакомство с данным свойством сводится к знакомству с правилом Умножение суммы на число:
Запишите это в тетрадь и щелкните мышкой по голубому полю экрана
Сформулируйте и запишите это правило.
Чтобы проверить себя щелкните мышкой по знаку вопроса.
Для продолжения работы щелкните мышкой по голубому полю экрана
Чтобы умножить сумму на число можно умножить на это число каждое слагаемое и полученные результаты сложить.
Например:
В четырех корзинах лежало по 3 яблока и 2 груши в каждой. Сколько всего фруктов лежало в корзинах?
Задание:
Решите задачу различными способами, записав решение выражением.
Запишите план решения задачи в каждом способе.
Запишите систему вопросов ученикам на сравнение полученных равенств, которые приведут их к выводу правила «Умножение суммы на число». Рядом с вопросами запишите предполагаемые ответы учеников.
Выполните это задание.
Для продолжения работы щелкните мышкой по управляющей кнопке.
Слайд 11Дистрибутивный закон умножения (продолжение)
Правило «Умножение суммы на число» используют для ознакомления с
Дистрибутивный закон умножения (продолжение)
Правило «Умножение суммы на число» используют для ознакомления с

27 ⋅ 3 =(20 + 7) ⋅ 3 =20 ⋅ 3 + 7 ⋅ 3 = 60 + 21= 81
Рассуждения ученика:
представляю число 27 в виде суммы разрядных (удобных) слагаемых 20 + 7;
нам удобно сначала 20 умножить на 3 – получится 60, а затем 7 умножить на 3 – получится 21;
к 60 прибавим 21 – получится 81.
Запишите это в тетрадь и щелкните мышкой по голубому полю экрана
Для продолжения работы щелкните мышкой по управляющей кнопке.
Задание:
Составьте свою задачу, иллюстрирующую правило Умножения суммы на число;
Решите ее различными способами, записав решение выражением.
Запишите план решения задачи в каждом способе.
Слайд 12Выполните это задание.
Для продолжения работы щелкните мышкой по голубому полю экрана.
Выполните это задание.
Для продолжения работы щелкните мышкой по голубому полю экрана.

Свойства умножения (продолжение)
Дистрибутивный закон умножения относительно вычитания
Для любых целых неотрицательных чисел а, b и с верно равенство:
(а – b) ⋅ с = а ⋅ с - b ⋅ с
(∀а,b,с ∈No) (а - b) ⋅ с = а ⋅ с - b ⋅ с
Данное правило в явном виде не изучается в начальной школе, но при решении задач разными способами, дети могут получить представление об этом правиле.
Этому свойству соответствует правило Умножение разности на число
Запишите это в тетрадь и щелкните мышкой по голубому полю экрана
Сформулируйте и запишите это правило.
Чтобы проверить себя щелкните мышкой по знаку вопроса.
Для продолжения работы щелкните мышкой по голубому полю экрана
Задание:
Решите составленную задачу различными способами, записав решение выражением.
Запишите план решения задачи в каждом способе.
Чтобы умножить разность на число, можно умножить на это число сначала уменьшаемое, а затем вычитаемое, и из первой разности вычесть вторую.
Задание: Составьте и запишите задачу по иллюстрации, которая появится на экране, так, чтобы с ее помощью можно было познакомиться с правилом Умножение разности на число. Для того, чтобы появилась иллюстрация задачи, щелкните мышкой по оранжевому кругу. При повторном щелчке действие повторится.
Для продолжения работы щелкните мышкой по зеленому полю экрана.
Правило «Умножение разности на число» можно использовать для показа следующего вычислительного приема:
29 ⋅ 3 =(30 – 1) ⋅ 3 =30 ⋅ 3 – 1 ⋅ 3 = 90 – 3 = 87
Задание: Запишите рассуждения ученика при решении примера таким способом.
Составьте два подобных примера и решите их.
Для продолжения работы щелкните мышкой по управляющей кнопке.
Слайд 13В выражении …, стоящем справа, первый множитель (не изменился, увеличился (уменьшился) в
В выражении …, стоящем справа, первый множитель (не изменился, увеличился (уменьшился) в

Свойства умножения (продолжение)
Свойство монотонности
Если один из множителей увеличить (уменьшить) в несколько раз, то и произведение увеличится (уменьшится) во столько же раз.
(∀а,b,с ∈No) (а > b) ⇒ а ⋅ с > b ⋅ с
В начальной школе знакомство с данным свойством происходит опосредовано при выполнении различных заданий, связанных с прямо-пропорциональной зависимостью. Например: 1. Заполни таблицу:
Выполняя это задание, дети замечают, что 1-ый множитель увеличивается, а 2-ой остается без изменения, при этом произведение также увеличивается
2. Какое произведение больше? Не вычисляя значения выражений, выясни во сколько раз одно произведение больше другого.
3 ⋅ 6 … 3 ⋅ 12
14 ⋅ 4 … 7 ⋅ 4
Запишите это в тетрадь и щелкните мышкой по голубому полю экрана
24 ⋅ 39 … 24 ⋅ 13
Выполните это задание. К какому выводу могут прийти ученики после его выполнения. Чтобы проверить себя щелкните мышкой по голубому полю экрана
Выполните это задание. Как могут рассуждать ученики при его выполнении. Чтобы проверить себя щелкните мышкой по голубому полю экрана
Выполните это задание.
Для продолжения работы щелкните мышкой по голубому полю экрана.
Для продолжения работы щелкните мышкой по управляющей кнопке.
Слайд 14Возврат в оглавление
Изучение умножения в начальном курсе математики
I этап. Ознакомление с умножением.
Возврат в оглавление
Изучение умножения в начальном курсе математики
I этап. Ознакомление с умножением.

с конкретным смыслом умножения – суммой одинаковых слагаемых. Результат действия умножения на этом этапе находят, заменяя умножение сложением. Например: 5 ⋅ 3 = 5 + 5 + 5 = 15;
с записью арифметического действия;
с чтением выражений. Например: 5 ⋅ 3: «Пять умножить на три», «Пять взять три раза».
знакомятся с названием компонентов «множитель» и «произведение».
После этого знакомства выражение 5 ⋅ 3 может быть прочитано: «Произведение пяти и трех», «Первый множитель – 5, второй – 3, найти произведение».
Запишите это в тетрадь и щелкните мышкой по голубому полю экрана
II этап. Изучение таблиц умножения. На этом этапе дети:
изучают переместительный закон умножения;
составляют и заучивают наизусть таблицы умножения чисел 2, 3, 4, 5, 6, 7, 8, 9. Каждая таблица начинается со случая умножения числа самого на себя;
знакомятся с особыми случаями умножения: умножение на 1; умножение на 0;
знакомятся с отношением «больше в …». После этого знакомства добавляются варианты чтения выражений. Например: 5 ⋅ 3: «Пять увеличить в три раза»;
III этап. Изучение приемов внетабличного умножения. На этом этапе дети знакомятся:
со свойствами умножения в явной или опосредованной форме;
с приемами внетабличного умножения:
умножение круглых чисел, например: 50 ⋅ 3. 5 ⋅ 30;
умножение двузначного числа на однозначное, например: 24 ⋅ 3;
Для продолжения работы щелкните мышкой по управляющей кнопке.
Задание: какое свойство лежит в основе каждого вычислительного приема?
Слайд 15Изучение умножения в НКМ (продолжение)
Запишите это в тетрадь и щелкните мышкой по
Изучение умножения в НКМ (продолжение)
Запишите это в тетрадь и щелкните мышкой по

IVэтап. Изучение приемов умножения чисел до 1000 и многозначных чисел. На этом этапе дети:
закрепляют вычислительные приемы умножения, основанные на знании свойств умножения. Например: 80 ⋅ 3, 84 ⋅ 4, 36 ⋅ 600, 3600 ⋅ 3;
Для продолжения работы вернитесь в оглавление.
Задание: запишите рассуждения учеников при решении каждого из этих примеров.
знакомятся с алгоритмами письменного умножения:
умножение многозначного числа на однозначное;
Выполните это задание.
Для продолжения работы щелкните мышкой по голубому полю экрана.
умножение многозначного числа на круглое число, содержащее только одну цифру, отличную от нуля;
умножение многозначного числа на двузначное, трехзначное, многозначное число;
умножение круглых многозначных чисел.
Задание: вычислите значения данных выражений.
Для знакомства с алгоритмами письменного умножения, щелкните по кнопке со знаком вопроса.
Для продолжения работы щелкните мышкой по голубому полю экрана.
Слайд 16Алгоритмы письменного умножения
Алгоритм умножения многозначного числа на однозначное:
Запишете второй множитель под разрядом
Алгоритмы письменного умножения
Алгоритм умножения многозначного числа на однозначное:
Запишете второй множитель под разрядом

Умножьте сначала единицы первого разряда.
а) Если полученное произведение меньше 10, то запишите его в соответствующий разряд ответа;
б) Если полученное произведение больше 10, то выделите в ответе полное количество десятков и оставшееся количество единиц. Полученные единицы запишите в соответствующий разряд ответа, а количество десятков перейдет в следующий разряд (их нужно запомнить);
3. Повторяйте те же действия со всеми разрядами числа, добавляя к полученному произведению запомненные единицы из предыдущих разрядов.
Алгоритм умножения многозначного числа на круглое число, содержащее только одну цифру, отличную от нуля:
Запишите это в тетрадь и щелкните мышкой по голубому полю экрана
Запишете второй множитель под первым так, чтобы его отличная от нуля значащая цифра стояла под разрядом единиц первого множителя.
Умножьте первый множитель на эту цифру по алгоритму умножения многозначного числа на однозначное
3. К полученному результату припишите столько нулей, сколько их было во втором множителе.
Для продолжения работы щелкните по управляющей кнопке.
Изучение умножения в НКМ (продолжение)
Слайд 17Запишите это в тетрадь и щелкните мышкой по голубому полю экрана
Алгоритм
Запишите это в тетрадь и щелкните мышкой по голубому полю экрана
Алгоритм

Запишете второй множитель под первым так, чтобы соответствующие разряды находились друг под другом;
Последовательно умножьте первый множитель сначала на единицы, потом на десятки, стони и т. д. второго множителя по алгоритму умножения многозначного числа на однозначное.
Полученные неполные произведения начинайте писать под тем разрядом, на который умножаете.
Если во втором множителе один из разрядов равен нулю, то умножение на этот разряд пропускается. При этом нужно помнить, что следующее неполное произведение нужно начать писать под тем разрядом, на цифру которого производится умножение.
3. Сложите полученные неполные произведения по алгоритму письменного сложения.
Алгоритм умножения круглых многозначных чисел:
Запишете второй множитель под первым так, чтобы первая справа отличная от нуля цифра второго множителя стояла под первой справа отличной от нуля цифрой первого множителя
Мысленно отбрасываем нули, стоящие в конце множителей и умножаем полученные числа по алгоритму умножения многозначного числа на многозначное.
3. К полученному результату приписываем столько нулей, сколько их было в двух множителях вместе.
Для продолжения работы щелкните по управляющей кнопке.
Алгоритмы письменного умножения (продолжение)
 30.01.2008 год. Тема урока: Семья в современном обществе Семья в жизни человека. Семья в современном обществе. Семейны
30.01.2008 год. Тема урока: Семья в современном обществе Семья в жизни человека. Семья в современном обществе. Семейны Л.Н. Толстой "После бала"
Л.Н. Толстой "После бала" Отварные мясные блюда
Отварные мясные блюда От понимания локальных конфликтов к использованию возможностей развития
От понимания локальных конфликтов к использованию возможностей развития Сюжеты Нового Завета
Сюжеты Нового Завета Имидж-карта танцора
Имидж-карта танцора Мастер стратегий
Мастер стратегий Производство фиточаев
Производство фиточаев Kaws 2
Kaws 2 Презентация на тему Второй закон Ньютона
Презентация на тему Второй закон Ньютона  Горький - романтик
Горький - романтик Управление по трендам вероятности успеха – действительно интегрированное управление сроками, стоимостью, ресурсами, содержанием
Управление по трендам вероятности успеха – действительно интегрированное управление сроками, стоимостью, ресурсами, содержанием Нижний Новгород
Нижний Новгород Поисковые системы сети Интернет
Поисковые системы сети Интернет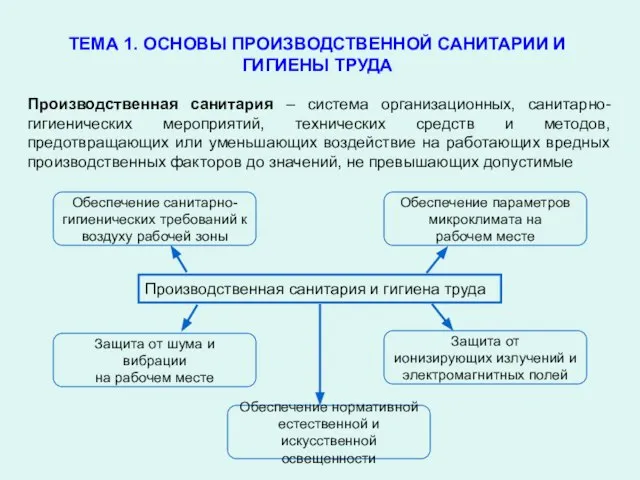 Основы производственной санитарии и гигиены труда
Основы производственной санитарии и гигиены труда Основы селекции растений, животных, микроорганизмов
Основы селекции растений, животных, микроорганизмов Помогает ли пунктуация в понимании содержания письменного текста?Что такое пунктуация? Когда она возникла?
Помогает ли пунктуация в понимании содержания письменного текста?Что такое пунктуация? Когда она возникла? Человек и закон. Конкурс лучших детективов имени Шерлока Холмса
Человек и закон. Конкурс лучших детективов имени Шерлока Холмса Жизнедеятельность клетки
Жизнедеятельность клетки Test №2
Test №2 Тигр
Тигр Квесторы. Бутерброд
Квесторы. Бутерброд Джинсы. История и современность
Джинсы. История и современность Презентация на тему Тест по культуре Индии
Презентация на тему Тест по культуре Индии  А. С. Пушкин « Сказка о мертвой царевне и о семи богатырях»
А. С. Пушкин « Сказка о мертвой царевне и о семи богатырях» Чугун и сталь
Чугун и сталь Тренинг для медицинских представителейETMS+
Тренинг для медицинских представителейETMS+ О проведении культурно-массовых мероприятий, посвященных празднованию Нового года и Рождества
О проведении культурно-массовых мероприятий, посвященных празднованию Нового года и Рождества