Содержание
- 2. «Ценить людей надо по тем целям, которые они перед собой ставят” Н.Н.Миклухо-Маклай.
- 3. Цель: повторить теорию, выработать умение определять вид уравнения и выбирать рациональный способ решения данного уравнения показать
- 4. Чтоб математику учить, Её сперва нужно любить.
- 5. ПРИМЕР: Разложим левую часть уравнения на множители: Ответ: -1; 1/6; 6. Проверьте
- 6. Сделаем замену: х2 +2х=t, тогда получили новое дробно-рациональное уравнение относительно t, которое можно свести к решению
- 7. Чтоб математику понять, Её детально нужно знать.
- 8. 1.Что такое уравнение? Равенство, содержащее неизвестное. 2.Что значит решить уравнение? Найти все его корни или доказать,
- 9. Решите уравнение: Х = 5 корней нет Х = 0; -3 Х = -3; 3 Х
- 10. х4 – 10 х2 + 9= 0
- 11. (х-10)2-3(х-10)-4=0
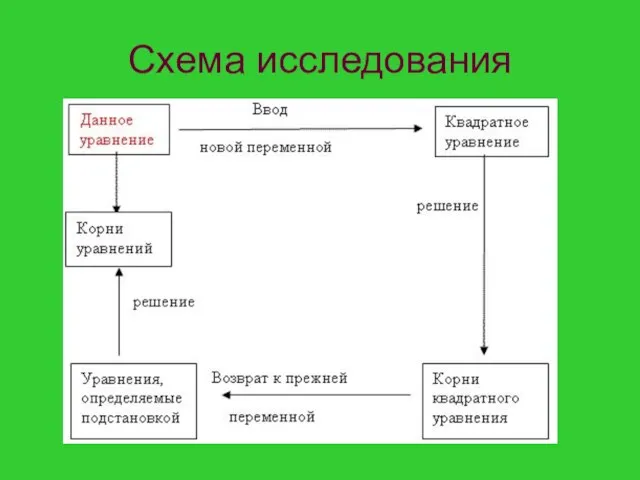
- 12. Схема исследования
- 13. Чтоб математикой увлечь, Вниманье нужно к ней привлечь.
- 14. Рассмотрим решение уравнений высших степеней, используя разложение на множители. ПРИМЕР: Разложим левую часть уравнения на множители:
- 15. Чтоб с математикой дружить, Во всем логичным нужно быть.
- 16. 1)(х-9)2-8(х-9)+7=0 а = х-9 2) (у2+2у+4) – 7(у2+2у+4)+12=0 а = у2+2у+4 3) (х2+х+1)2- 3х2- 3х- 3=0
- 17. 1)(х-9)2-8(х-9)+7=0
- 18. 4) 4(х2-5х+7) - (х-2)(х-3)=1
- 20. Самостоятельная работа Вариант 1 «3» 1) Х 3-64х=0 2) Х4 -5х2 +4=0 3) Х3 +х2 -х-1=0
- 21. 2.Ответ: -1; 1; 3 Вариант 3 «5» 1. Ответ: -2; 2 3. Ответ: -3; 2 Решение
- 22. Дома: Сборник ГИА-9 2010г. стр. 151 №128;129;130;131.
- 24. Скачать презентацию








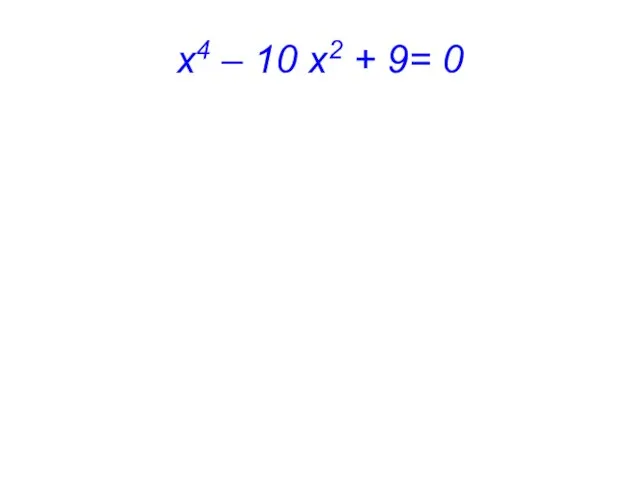
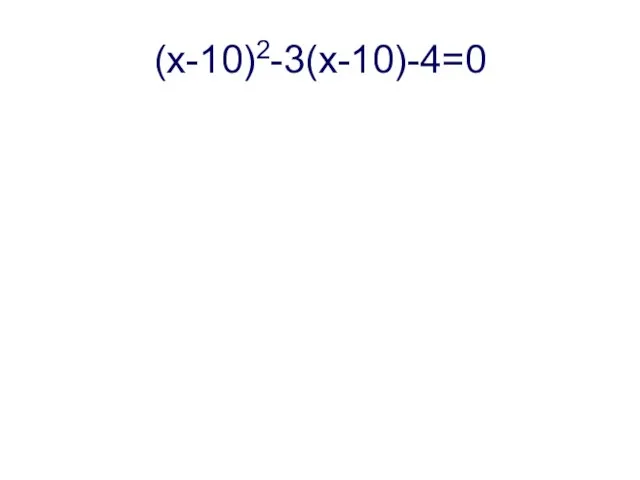



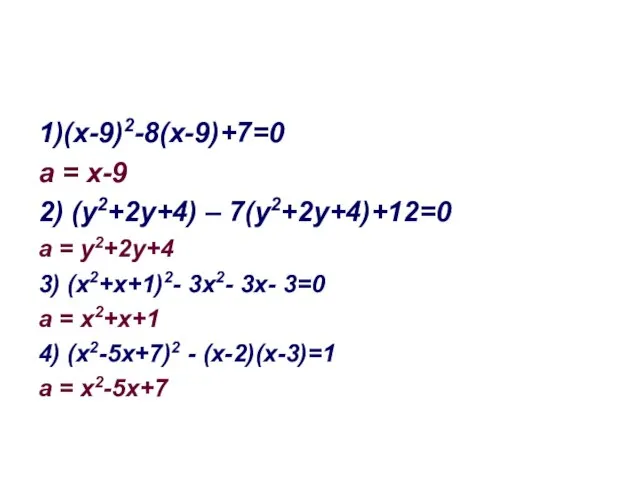

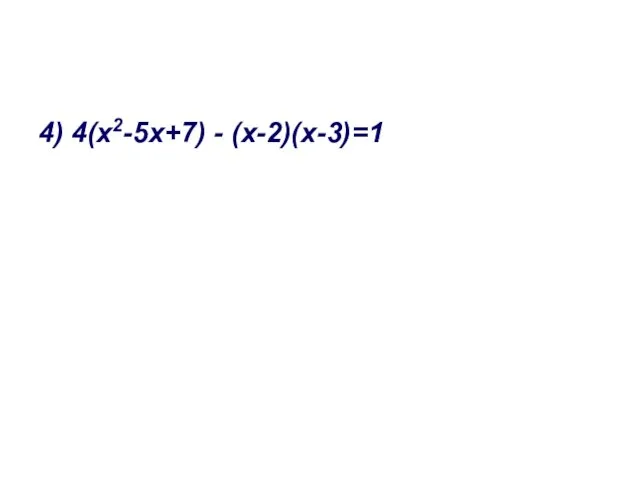




 Абузярова Луиза Ибрагимовна
Абузярова Луиза Ибрагимовна Teatro Colon
Teatro Colon Организация образовательной деятельности в условиях ФГОС для обучающихся с ОВЗ
Организация образовательной деятельности в условиях ФГОС для обучающихся с ОВЗ Прогресс-Гарант
Прогресс-Гарант Мы рады приветствовать вас в группе компаний ПИК
Мы рады приветствовать вас в группе компаний ПИК ВКР: Геодезические работы при строительстве СПГ Портовая
ВКР: Геодезические работы при строительстве СПГ Портовая Детское объединение Юность
Детское объединение Юность Правила дорожного движения для пешехода
Правила дорожного движения для пешехода Эмблема ООН
Эмблема ООН Природные сообщества
Природные сообщества Противодействие утечкам конфиденциальной информации и персональных данных
Противодействие утечкам конфиденциальной информации и персональных данных Мультиспонсорский проект «Междисциплинарный подход в терапии внутренних болезней»
Мультиспонсорский проект «Междисциплинарный подход в терапии внутренних болезней» Типы ВНД. Запольская М. Борзых Ю
Типы ВНД. Запольская М. Борзых Ю Работа выполнена в рамках проекта «Повышение квалификаций различных категорий работников образования и формирование у них базов
Работа выполнена в рамках проекта «Повышение квалификаций различных категорий работников образования и формирование у них базов Олимпиада школьников Ломоносов по психологии
Олимпиада школьников Ломоносов по психологии Презентация на тему Напряжение
Презентация на тему Напряжение Cтивен Р. Кови Принцип-центричное руководство
Cтивен Р. Кови Принцип-центричное руководство Russian presidential academy of the national economy and public admistration noth-west institute of management municipal
Russian presidential academy of the national economy and public admistration noth-west institute of management municipal Шагаа сүзүктери
Шагаа сүзүктери Класификация товаров
Класификация товаров Was machen wir in der Freizeit
Was machen wir in der Freizeit Основы теории конечных автоматов
Основы теории конечных автоматов Наука и полёт фантазии (анализ главы 12 из романа «Затерянный мир»)
Наука и полёт фантазии (анализ главы 12 из романа «Затерянный мир») Воображение и творчество
Воображение и творчество «Тропинка, кочки, копна»
«Тропинка, кочки, копна» Kochaj mnie
Kochaj mnie yfvhyt
yfvhyt Еда и напитки, не выходя из офиса
Еда и напитки, не выходя из офиса